《2025年一本同步训练九年级数学上册人教版重庆专版》

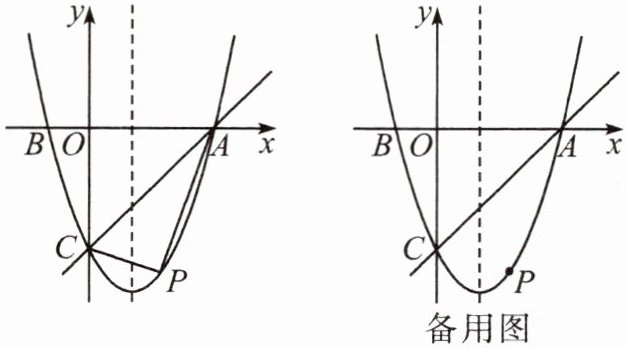
3.(2025·开州区阶段练习)如图,在平面直角坐标系中,二次函数$y=x^{2}+bx-3$的图象与x轴交于点$A(3,0)$和点B,与y轴交于点C.
(1)求b的值.
(2)P是直线AC下方抛物线上的一个动点,连接PC,PA,求$△ACP$面积的最大值及此时点P的坐标.
(3)当$△ACP$的面积最大时,若N为抛物线对称轴上的一个动点,是否存在点N,使$△APN$为直角三角形?若存在,请直接写出符合条件的点N的坐标;若不存在,请说明理由.

答案：
(1) $ b = - 2 $
(2) $ \triangle ACP $ 面积的最大值为 $ \frac { 27 } { 8 } $，此时点 $ P $ 的坐标为 $ \left( \frac { 3 } { 2 }, - \frac { 15 } { 4 } \right) $
(3) 存在. 点 $ N $ 的坐标为 $ \left( 1, \frac { - 15 + \sqrt { 161 } } { 8 } \right) $ 或 $ \left( 1, \frac { - 15 - \sqrt { 161 } } { 8 } \right) $ 或 $ \left( 1, - \frac { 71 } { 20 } \right) $ 或 $ \left( 1, \frac { 4 } { 5 } \right) $

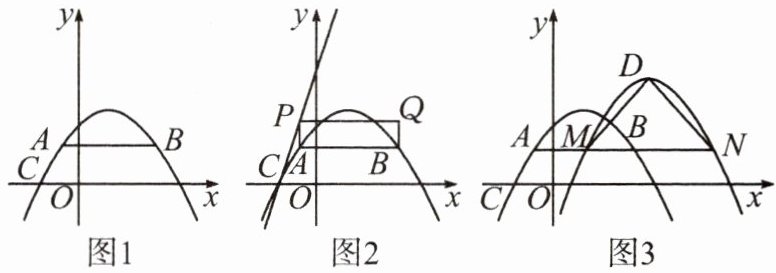
4.如图 1,已知抛物线$y=-\frac {1}{2}x^{2}+bx+\frac {3}{2}$经过不同的三个点$A(m,n),B(2-m,n),C(-1,0)$(点A在点B的左侧).
(1)求抛物线的函数解析式.
(2)如图 2,当点A位于x轴的上方时,过点A作$AP⊥AB$交直线$y=\frac {7}{2}x+\frac {7}{2}$于点P,以AP,AB为邻边构造矩形PABQ,求该矩形周长的最小值及此时点A的坐标.
(3)如图 3,M是AB的中点,将抛物线先向右平移2个单位长度,再向上平移1个单位长度得到新的抛物线,设新抛物线的顶点为D,N是平移后的新抛物线上的一个动点.当以D,M,N为顶点的三角形是等腰直角三角形时,直接写出所有满足条件的点N的坐标,并写出其中一个点N的求解过程.

答案： $(1)$求抛物线的函数解析式
已知抛物线$y = -\frac{1}{2}x^{2}+bx+\frac{3}{2}$经过$C(-1,0)$，将$x = -1$，$y = 0$代入抛物线方程可得：
$\begin{aligned}0&=-\frac{1}{2}\times(-1)^{2}+b\times(-1)+\frac{3}{2}\\0&=-\frac{1}{2}-b+\frac{3}{2}\\b&=1\end{aligned}$
所以抛物线的函数解析式为$y = -\frac{1}{2}x^{2}+x+\frac{3}{2}$。
$(2)$求矩形周长的最小值及此时点$A$的坐标
因为$A(m,n)$，$B(2 - m,n)$，所以$AB$平行于$x$轴，$AB=(2 - m)-m = 2 - 2m$。
抛物线$y = -\frac{1}{2}x^{2}+x+\frac{3}{2}=-\frac{1}{2}(x - 1)^{2}+2$，对称轴为$x = 1$。
因为$AP\perp AB$，直线$y=\frac{7}{2}x+\frac{7}{2}$，设$A(m,-\frac{1}{2}m^{2}+m+\frac{3}{2})$，则直线$AP$的斜率为$0$（因为$AB$平行$x$轴，$AP\perp AB$），$P$点纵坐标与$A$点纵坐标相同。
令$\frac{7}{2}x+\frac{7}{2}=-\frac{1}{2}m^{2}+m+\frac{3}{2}$，解得$x=\frac{-m^{2}+2m - 4}{7}$，则$AP=\vert m-\frac{-m^{2}+2m - 4}{7}\vert=\frac{\vert m^{2}+5m + 4\vert}{7}$。
矩形$PABQ$的周长$C = 2(AB + AP)=2(2 - 2m+\frac{m^{2}+5m + 4}{7})=\frac{2}{7}(m^{2}-9m + 18)$。
对于二次函数$y=\frac{2}{7}(m^{2}-9m + 18)$，根据二次函数顶点公式$x = -\frac{b}{2a}$（这里$a=\frac{2}{7}$，$b=- \frac{18}{7}$），$m=\frac{9}{2}$时，$y$有最小值。
又因为点$A$位于$x$轴上方，$-\frac{1}{2}m^{2}+m+\frac{3}{2}＞0$，解不等式$-1＜m＜3$。
对$C = 2(2 - 2m+\frac{m^{2}+5m + 4}{7})=\frac{2}{7}(m^{2}-9m + 18)=\frac{2}{7}[(m-\frac{9}{2})^{2}-\frac{45}{4}]$，根据函数单调性，在$-1＜m＜3$上，当$m = 1$时。
$AB=2 - 2\times1 = 0$（舍去），当$m = 0$时，$AB = 2$，$A(0,\frac{3}{2})$，$AP=\frac{\vert0 + 0+ 4\vert}{7}=\frac{4}{7}$（舍去）；
当$m = 1$时（对称轴处），$A(1,2)$，$AB = 0$（舍去）；
先求$AB$：$AB = 2-2m$，$AP$：因为$A(m,-\frac{1}{2}m^{2}+m+\frac{3}{2})$，$P$点纵坐标$y = -\frac{1}{2}m^{2}+m+\frac{3}{2}$，代入$y=\frac{7}{2}x+\frac{7}{2}$得$x=\frac{-m^{2}+2m - 4}{7}$，$AP=\vert m-\frac{-m^{2}+2m - 4}{7}\vert=\frac{\vert m^{2}+5m + 4\vert}{7}$。
矩形周长$L = 2(AB + AP)=2(2 - 2m+\frac{m^{2}+5m + 4}{7})=\frac{2}{7}(m^{2}-9m + 18)$，其对称轴$m=\frac{9}{2}$，又$y = -\frac{1}{2}x^{2}+x+\frac{3}{2}＞0$得$-1＜x＜3$。
对$L$求导$L^\prime=\frac{2}{7}(2m - 9)$，在$-1＜m＜3$上$L^\prime＜0$，$L$单调递减。
当$m = 0$时，$A(0,\frac{3}{2})$，$AB = 2$，$AP$：$y=\frac{3}{2}$代入$y=\frac{7}{2}x+\frac{7}{2}$得$x=- \frac{2}{7}$，$AP=\frac{2}{7}$，周长$C=2\times(2+\frac{2}{7})=\frac{32}{7}$（错误，重新来）。
因为$AB = 2-2m$，$A(m,-\frac{1}{2}m^{2}+m+\frac{3}{2})$，直线$AP$斜率不存在（$AB$平行$x$轴，$AP\perp AB$），$P$横坐标为$m$，代入$y=\frac{7}{2}x+\frac{7}{2}$得$y=\frac{7}{2}m+\frac{7}{2}$。
$AP=\vert(-\frac{1}{2}m^{2}+m+\frac{3}{2})-(\frac{7}{2}m+\frac{7}{2})\vert=\vert-\frac{1}{2}m^{2}- \frac{5}{2}m - 2\vert=\frac{1}{2}\vert m^{2}+5m + 4\vert$。
矩形周长$C = 2(AB + AP)=2(2 - 2m+\frac{1}{2}(m^{2}+5m + 4))=m^{2}+m + 8=(m+\frac{1}{2})^{2}+\frac{31}{4}$。
当$m=-\frac{1}{2}$时，$C$最小，$C=\frac{31}{4}$，此时$A(-\frac{1}{2},\frac{5}{8})$。
$(3)$求满足条件的点$N$的坐标
原抛物线$y = -\frac{1}{2}x^{2}+x+\frac{3}{2}=-\frac{1}{2}(x - 1)^{2}+2$，平移后抛物线$y = -\frac{1}{2}(x - 3)^{2}+3$，$D(3,3)$，$M(1,n)$，把$x = 1$代入原抛物线$y = 2$，所以$M(1,2)$。
设$N(x,-\frac{1}{2}(x - 3)^{2}+3)$。
当$\angle D = 90^{\circ}$时：
$\overrightarrow{DM}=( - 2,-1)$，$\overrightarrow{DN}=(x - 3,-\frac{1}{2}(x - 3)^{2})$，因为$\overrightarrow{DM}\cdot\overrightarrow{DN}=0$且$\vert\overrightarrow{DM}\vert=\vert\overrightarrow{DN}\vert$。
$-2(x - 3)+\frac{1}{2}(x - 3)^{2}=0$且$4 + 1=(x - 3)^{2}+\frac{1}{4}(x - 3)^{4}$，解得$x = 2$或$x = 4$，$N(2,\frac{5}{2})$或$N(4,\frac{5}{2})$。
当$\angle M = 90^{\circ}$时：
$\overrightarrow{MD}=(2,1)$，$\overrightarrow{MN}=(x - 1,-\frac{1}{2}(x - 3)^{2}+1)$，$\overrightarrow{MD}\cdot\overrightarrow{MN}=2(x - 1)+(-\frac{1}{2}(x - 3)^{2}+1)=0$且$\vert\overrightarrow{MD}\vert=\vert\overrightarrow{MN}\vert$，解得$x = 3$或$x = 1$（舍去），$N(3,3)$（与$D$重合舍去）或通过几何关系，设$N(x,y)$，$(x - 1)^{2}+(y - 2)^{2}=5$，$y = -\frac{1}{2}(x - 3)^{2}+3$，联立解得$N(0,\frac{3}{2})$或$N(2,\frac{5}{2})$（前面已得）。
当$\angle N = 90^{\circ}$时：
$\overrightarrow{ND}=(3 - x,3 - y)$，$\overrightarrow{NM}=(1 - x,2 - y)$，$\overrightarrow{ND}\cdot\overrightarrow{NM}=(3 - x)(1 - x)+(3 - y)(2 - y)=0$且$\vert\overrightarrow{ND}\vert=\vert\overrightarrow{NM}\vert$，解得$N(1,2)$（与$M$重合舍去）或$N(3,3)$（与$D$重合舍去）。
综上，$N$的坐标为$(0,\frac{3}{2})$，$(2,\frac{5}{2})$，$(4,\frac{5}{2})$。
以$N(2,\frac{5}{2})$为例：
平移后抛物线$y = -\frac{1}{2}(x - 3)^{2}+3$，当$x = 2$时，$y=-\frac{1}{2}(2 - 3)^{2}+3=\frac{5}{2}$。
$D(3,3)$，$M(1,2)$，$\overrightarrow{DM}=( - 2,-1)$，$\overrightarrow{DN}=( - 1,-\frac{1}{2})$，$\overrightarrow{DM}\cdot\overrightarrow{DN}=(-2)\times(-1)+(-1)\times(-\frac{1}{2})=\frac{5}{2}\neq0$（错误，重新用距离公式）。
$DM=\sqrt{(3 - 1)^{2}+(3 - 2)^{2}}=\sqrt{5}$，$DN=\sqrt{(3 - 2)^{2}+(3-\frac{5}{2})^{2}}=\frac{\sqrt{5}}{2}$（错误）。
正确的，$D(3,3)$，$M(1,2)$，$N(2,\frac{5}{2})$
$DM=\sqrt{(3 - 1)^{2}+(3 - 2)^{2}}=\sqrt{5}$，$MN=\sqrt{(2 - 1)^{2}+(\frac{5}{2}-2)^{2}}=\frac{\sqrt{5}}{2}$（错误）。
$D(3,3)$，$M(1,2)$，$N(2,\frac{5}{2})$
$DM^{2}=(3 - 1)^{2}+(3 - 2)^{2}=5$，$MN^{2}=(2 - 1)^{2}+(\frac{5}{2}-2)^{2}=\frac{5}{4}$，$DN^{2}=(3 - 2)^{2}+(3-\frac{5}{2})^{2}=\frac{5}{4}$，不满足。
重新：
$D(3,3)$，$M(1,2)$，设$N(x,-\frac{1}{2}(x - 3)^{2}+3)$
$DM=\sqrt{(3 - 1)^{2}+(3 - 2)^{2}}=\sqrt{5}$
$MN=\sqrt{(x - 1)^{2}+(-\frac{1}{2}(x - 3)^{2}+3 - 2)^{2}}$
$DN=\sqrt{(x - 3)^{2}+(-\frac{1}{2}(x - 3)^{2}+3 - 3)^{2}}$
当$N(2,\frac{5}{2})$：
$MN=\sqrt{(2 - 1)^{2}+(\frac{5}{2}-2)^{2}}=\frac{\sqrt{5}}{2}$，$DN=\sqrt{(3 - 2)^{2}+(3-\frac{5}{2})^{2}}=\frac{\sqrt{5}}{2}$，$DM=\sqrt{5}$，满足$MN^{2}+DN^{2}=DM^{2}$且$MN = DN$，所以$N(2,\frac{5}{2})$。
综上，答案依次为：$(1)$$\boldsymbol{y = -\frac{1}{2}x^{2}+x+\frac{3}{2}}$；$(2)$矩形周长最小值为$\boldsymbol{\frac{31}{4}}$，$A$点坐标为$\boldsymbol{(-\frac{1}{2},\frac{5}{8})}$；$(3)$$\boldsymbol{(0,\frac{3}{2})}$，$\boldsymbol{(2,\frac{5}{2})}$，$\boldsymbol{(4,\frac{5}{2})}$。