《2025年一本同步训练九年级数学上册人教版重庆专版》

1.(2024·连云港)如图,将一根木棒的一端固定在O点,另一端绑一重物.将此重物拉到A点后放开,让此重物由A点摆动到B点,则此重物移动路径的形状为 (C)

A.倾斜直线
B.抛物线
C.圆弧
D.水平直线

答案： C

2.已知$\odot O$中的弦最长为16 cm,则$\odot O$的半径是 (B)
A.4 cm
B.8 cm
C.16 cm
D.32 cm

答案： B

[变式] 若AB是半径为2的圆的一条弦,则AB的长不可能是 (D)
A.2
B.3
C.4
D.5

答案： D

3.下列命题中,正确的是 (C)
①半圆是弧;②弦是圆上两点之间的部分;③半径是弦;④在同圆或等圆中,直径是最长的弦;⑤在同一平面内,到定点的距离等于定长的点都在同一个圆上.
A.①②③
B.①③④
C.①④⑤
D.②④⑤

答案： C

4.(2025·重庆一中期中改编)如图,AB为$\odot O$的直径,点C,D在$\odot O$上,已知$∠AOD=40^{\circ },AD// OC$,则$∠COD$的度数是______70°.

答案： 70°

5.如图,A,B,C是$\odot O$上的三点,$∠A=80^{\circ },∠C=60^{\circ }$,则$∠B$的度数为______140°.

答案： 140°

6.如图,点A,B,C在$\odot O$上.若$∠A=40^{\circ },∠C=20^{\circ }$,则$∠B=$60°.

答案： 60

7.如图,在$\odot O$中,AB为直径,$CD⊥AB$于点C,四边形CDEF是正方形,连接BD.若$CO=3,OF=1$,则$BD=$4√5.

答案： 4√5

8.如图,$\odot O$的弦AB,CD的延长线交于点P,连接OP,且PO平分$∠APC$.求证:$PA=PC$.

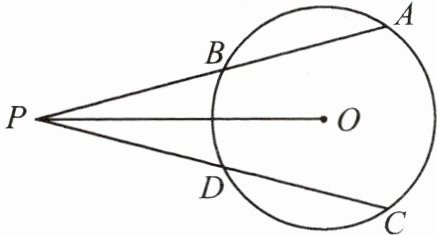
答案： 【解析】：
过点$O$作$OE\perp AB$于点$E$，$OF\perp CD$于点$F$。
因为$PO$平分$\angle APC$，$OE\perp AB$，$OF\perp CD$，根据角平分线的性质可知$OE = OF$。
在$\odot O$中，弦心距相等则弦相等，所以$AB = CD$。
又因为$OE\perp AB$，所以$AE=\frac{1}{2}AB$（垂径定理）；同理$CF=\frac{1}{2}CD$，所以$AE = CF$。
在$Rt\triangle POE$和$Rt\triangle POF$中，$\left\{\begin{array}{l}OE = OF\\OP = OP\end{array}\right.$，所以$Rt\triangle POE\cong Rt\triangle POF(HL)$，则$PE = PF$。
因为$PA=PE + AE$，$PC=PF + CF$，且$AE = CF$，$PE = PF$，所以$PA = PC$。
【答案】：
$PA = PC$得证。