2025年热搜题高中数学必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年热搜题高中数学必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第98页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. [2024·北京汇文中学月考](多选)下列结论中正确的有(
A.半圆弧以其直径所在的直线为轴旋转一周所形成的曲面叫做球
B.直角三角形以一条直角边所在的直线为轴,其余各边旋转一周形成的面所围成的旋转体是圆锥
C.夹在圆柱的两个平行截面间的几何体还是一个旋转体
D.圆锥截去一个小圆锥后剩余的部分是圆台
BD
)A.半圆弧以其直径所在的直线为轴旋转一周所形成的曲面叫做球
B.直角三角形以一条直角边所在的直线为轴,其余各边旋转一周形成的面所围成的旋转体是圆锥
C.夹在圆柱的两个平行截面间的几何体还是一个旋转体
D.圆锥截去一个小圆锥后剩余的部分是圆台
答案:
1.BD【解析】半圆弧以其直径所在的直线为轴旋转一周所形成的曲面叫做球面,球面围成的几何体叫做球,故A错误;以直角三角形的直角边所在直线为轴,其余各边旋转一周形成的面所围成的几何体是圆锥,故B正确;当两个平行截面不平行于上、下两个底面时,两个平行截面间的几何体不是旋转体,故C错误;将圆锥截去小圆锥,则截面必须与底面平行,因而剩余部分是圆台,故D正确.故选BD.
易错警示
本题易忽视球与球面的区别而错选A,或者忽视两个平行截面不平行于圆柱上、下两个底面的情况而错选C.
易错警示
本题易忽视球与球面的区别而错选A,或者忽视两个平行截面不平行于圆柱上、下两个底面的情况而错选C.
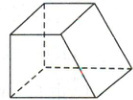
2. [2024·曲靖一中月考]如图所示,关于该几何体的说法正确的有
①这是一个六面体;
②这是一个四棱台;
③这是一个四棱柱;
④此几何体可由三棱柱截去一个三棱柱得到;
⑤此几何体可由四棱柱截去一个三棱柱得到。
①③④⑤
。(填序号)①这是一个六面体;
②这是一个四棱台;
③这是一个四棱柱;
④此几何体可由三棱柱截去一个三棱柱得到;
⑤此几何体可由四棱柱截去一个三棱柱得到。

答案:
2.①③④⑤【解析】①正确,因为有六个面,属于六面体的范围;②错误,因为侧棱的延长线不能交于一点,所以不正确;③正确,如果把几何体放倒,会发现是一个四棱柱;④⑤都正确,如图所示.


易错警示
判断棱台时经常会忽视侧棱的延长线必须交于一点这一特征,直观的感觉是棱台,而不注意逻辑推理;截多面体易忽视图形的多样性,要思考全面.
2.①③④⑤【解析】①正确,因为有六个面,属于六面体的范围;②错误,因为侧棱的延长线不能交于一点,所以不正确;③正确,如果把几何体放倒,会发现是一个四棱柱;④⑤都正确,如图所示.


易错警示
判断棱台时经常会忽视侧棱的延长线必须交于一点这一特征,直观的感觉是棱台,而不注意逻辑推理;截多面体易忽视图形的多样性,要思考全面.
3. [2024·广东实验中学期中](多选)如图,在直角梯形ABCD中,AB=2,CD=4,AD=2,则(
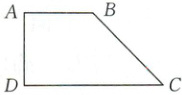
A.以AD所在直线为旋转轴,将此梯形旋转一周,所得几何体的侧面积为16√2π
B.以CD所在直线为旋转轴,将此梯形旋转一周,所得几何体的体积为32π/3
C.以AB所在直线为旋转轴,将此梯形旋转一周,所得几何体的表面积为20π+4√2π
D.以BC所在直线为旋转轴,将此梯形旋转一周,所得几何体的体积为28√2π/3
BCD
)
A.以AD所在直线为旋转轴,将此梯形旋转一周,所得几何体的侧面积为16√2π
B.以CD所在直线为旋转轴,将此梯形旋转一周,所得几何体的体积为32π/3
C.以AB所在直线为旋转轴,将此梯形旋转一周,所得几何体的表面积为20π+4√2π
D.以BC所在直线为旋转轴,将此梯形旋转一周,所得几何体的体积为28√2π/3
答案:
3.BCD【解析】延长DA,CB交于点E,如图1.
由题意得,AE=AD=2,
BE=BC=√AD²+$\frac{CD}{2}$( )=2$\sqrt{2}$.
对于A,以AD所在直线为轴旋转,得到一个圆台,此圆台的侧面积S侧=
(2+4)×2$\sqrt{2}$π=12$\sqrt{2}$π,故A错误;对
于B,以CD所在直线为轴旋转,得到一个以2为底面半径,以2为高的圆柱与一个以2为底面半径,以2为高的圆锥的组合体,所以该组合体的体积为V=V柱+V锥=2²×2π+$\frac{1}{3}$×2²×2π=$\frac{32π}{3}$,故B正确;对于C,以
AB所在直线为轴旋转,得到一个圆柱挖去一个圆锥的几何体,所以该几何体的表面积为S=
4π+2π×2×4+2$\sqrt{2}$×2π=20π+
4$\sqrt{2}$π,故C正确;对于D,以BC所在直
线为轴旋转,得到一个圆锥和一个圆台
 挖去一个小圆锥的几何体,如图2,所以
挖去一个小圆锥的几何体,如图2,所以
该几何体的体积为V=$\frac{1}{3}$×(2$\sqrt{2}$)²×
2$\sqrt{2}$π+$\frac{π}{3}$×[($\sqrt{2}$)²+$\sqrt{2}$×2$\sqrt{2}$+(2$\sqrt{2}$)²]×$\sqrt{2}$−$\frac{1}{3}$×($\sqrt{2}$)²×$\sqrt{2}$π=$\frac{28\sqrt{2}}{3}$π,故D正确.故选BCD.

易错警示
几何体的表面积是各个面的面积之和,因此,求组合体的表面积时切忌直接套用柱体、锥体、台体、球体的表面积公式,而应先分析该几何体由几部分组成,几何体各个面间有无重叠,再结合相应几何体选择公式求解.
3.BCD【解析】延长DA,CB交于点E,如图1.
由题意得,AE=AD=2,
BE=BC=√AD²+$\frac{CD}{2}$( )=2$\sqrt{2}$.
对于A,以AD所在直线为轴旋转,得到一个圆台,此圆台的侧面积S侧=
(2+4)×2$\sqrt{2}$π=12$\sqrt{2}$π,故A错误;对
于B,以CD所在直线为轴旋转,得到一个以2为底面半径,以2为高的圆柱与一个以2为底面半径,以2为高的圆锥的组合体,所以该组合体的体积为V=V柱+V锥=2²×2π+$\frac{1}{3}$×2²×2π=$\frac{32π}{3}$,故B正确;对于C,以
AB所在直线为轴旋转,得到一个圆柱挖去一个圆锥的几何体,所以该几何体的表面积为S=
4π+2π×2×4+2$\sqrt{2}$×2π=20π+
4$\sqrt{2}$π,故C正确;对于D,以BC所在直
线为轴旋转,得到一个圆锥和一个圆台
 挖去一个小圆锥的几何体,如图2,所以
挖去一个小圆锥的几何体,如图2,所以该几何体的体积为V=$\frac{1}{3}$×(2$\sqrt{2}$)²×
2$\sqrt{2}$π+$\frac{π}{3}$×[($\sqrt{2}$)²+$\sqrt{2}$×2$\sqrt{2}$+(2$\sqrt{2}$)²]×$\sqrt{2}$−$\frac{1}{3}$×($\sqrt{2}$)²×$\sqrt{2}$π=$\frac{28\sqrt{2}}{3}$π,故D正确.故选BCD.

易错警示
几何体的表面积是各个面的面积之和,因此,求组合体的表面积时切忌直接套用柱体、锥体、台体、球体的表面积公式,而应先分析该几何体由几部分组成,几何体各个面间有无重叠,再结合相应几何体选择公式求解.
4. [2024·太原一中月考]分别和两条异面直线相交的两条不同直线的位置关系是(
A.相交
B.异面
C.异面或相交
D.平行
C
)A.相交
B.异面
C.异面或相交
D.平行
答案:
4.C【解析】分两类进行讨论.
①若两条直线与两异面直线的交点有4个,如图1,直线
AB与异面直线a,b分别相交于点A,B,直线CD与异面直线a,b分别相交于点C,D,那么A,B,C,D四点不可能共面,否则与a,b异面矛盾,故直线AB与CD异面;


②若两条直线与两异面直线的交点有3个,如图2,两条直线相交.故选C.
误区警示
解题时易忽略两条直线与两异面直线的交点有3个的情况,认为交点只有4个,此时两条直线异面,从而错选B.
在立体几何中,空间点、直线、平面之间的位置关系不确定时,要注意分类讨论,避免片面地思考问题.在判断两条直线的位置关系时,可通过画出相关图形帮助分析.
4.C【解析】分两类进行讨论.
①若两条直线与两异面直线的交点有4个,如图1,直线
AB与异面直线a,b分别相交于点A,B,直线CD与异面直线a,b分别相交于点C,D,那么A,B,C,D四点不可能共面,否则与a,b异面矛盾,故直线AB与CD异面;


②若两条直线与两异面直线的交点有3个,如图2,两条直线相交.故选C.
误区警示
解题时易忽略两条直线与两异面直线的交点有3个的情况,认为交点只有4个,此时两条直线异面,从而错选B.
在立体几何中,空间点、直线、平面之间的位置关系不确定时,要注意分类讨论,避免片面地思考问题.在判断两条直线的位置关系时,可通过画出相关图形帮助分析.
5. [2024·成都七中月考]四棱柱ABCD-A₁B₁C₁D₁的底面是平行四边形,过此四棱柱任意两条棱的中点作直线,其中与平面DBB₁D₁平行的直线共有(
A.4条
B.6条
C.8条
D.12条
D
)A.4条
B.6条
C.8条
D.12条
答案:
5.D【解析】如图,设E,F,H,
G,P,Q,M,N分别为所在棱
的中点,因为P,N分别是

C₁D₁,B₁C₁的中点,所以PN//
B₁D₁.因为PN⊄平面
DBB₁D₁,B₁D₁⊂平面DBB₁D₁,
所以PN//平面DBB₁D₁.同理可证GF//平面
DBB₁D₁.因为四边形BCC₁B₁是平行四边形,N,F分别是B₁C₁,BC的中点,所以四边形BB₁NF是平行四边形,所以NF//BB₁.又因为NF⊄平面DBB₁D₁,BB₁⊂平面DBB₁D₁,所以NF//平面DBB₁D₁.同理可证PG//平面DBB₁D₁.又因为PN∩NF=N,所以平面PNFG//平面DBB₁D₁.因为PF⊂平面PNFG,NG⊂平面PNFG,所以PF//平面DBB₁D₁,NG//平面
DBB₁D₁.同理可证QM,ME,EH,HQ,QE,MH也与平面DBB₁D₁平行,共有12条直线.
易错警示
本题易忽视两个平面平行,其中一个平面内的所有直线与另一个平面平行,从而漏掉PF,NG,HM,QE四条与平面DBB₁D₁平行的直线,导致错解.
5.D【解析】如图,设E,F,H,
G,P,Q,M,N分别为所在棱
的中点,因为P,N分别是

C₁D₁,B₁C₁的中点,所以PN//
B₁D₁.因为PN⊄平面
DBB₁D₁,B₁D₁⊂平面DBB₁D₁,
所以PN//平面DBB₁D₁.同理可证GF//平面
DBB₁D₁.因为四边形BCC₁B₁是平行四边形,N,F分别是B₁C₁,BC的中点,所以四边形BB₁NF是平行四边形,所以NF//BB₁.又因为NF⊄平面DBB₁D₁,BB₁⊂平面DBB₁D₁,所以NF//平面DBB₁D₁.同理可证PG//平面DBB₁D₁.又因为PN∩NF=N,所以平面PNFG//平面DBB₁D₁.因为PF⊂平面PNFG,NG⊂平面PNFG,所以PF//平面DBB₁D₁,NG//平面
DBB₁D₁.同理可证QM,ME,EH,HQ,QE,MH也与平面DBB₁D₁平行,共有12条直线.
易错警示
本题易忽视两个平面平行,其中一个平面内的所有直线与另一个平面平行,从而漏掉PF,NG,HM,QE四条与平面DBB₁D₁平行的直线,导致错解.
6. [2024·重庆巴蜀中学月考]如图,点P在正方体ABCD-A₁B₁C₁D₁的面对角线BC₁上运动,有下面四个结论:①三棱锥A-D₁PC的体积不变;②A₁P//平面ACD₁;③DP⊥BC₁;④平面PDB₁⊥平面ACD₁。其中结论正确的有

①②④
。(填序号)
答案:
6.①②④【解析】如图1,连接AC,A₁C₁,A₁B,A₁P,
AD₁,D₁C.因为AA₁//CC₁,AA₁=CC₁,所以四边形
AA₁C₁C是平行四边形,所以AC//A₁C₁.又因为AC⊄平面A₁BC,A₁C₁⊂平面A₁BC,所以AC//平面
A₁BC.同理可证AD₁//平面A₁BC,又因为AC⊂平面
ACD₁,AD₁⊂平面ACD₁,且AC∩AD₁=A,所以平面
ACD₁//平面A₁BC.因为A₁P⊂平面A₁BC,所以A₁P//平面ACD₁,故②正确.因为BC//AD₁,所以BC//平面
ACD₁,所以点P到平面ACD₁的距离不变;又因为V三棱锥A₁−D₁PC=V三棱锥P−ACD₁,所以三棱锥A₁−D₁PC的体积不变,故①正确.


如图2,连接DB₁,DC₁,DP.因为DB₁=DC₁,所以当P为
BC₁的中点时才有DP⊥BC₁,故③错误.因为
BB₁⊥平面ABCD,AC⊂平面ABCD,所以AC⊥BB₁.又因为
AC⊥BD,BB₁∩BD=B,所以AC⊥平面BB₁D₁D.连接B₁D.因为B₁D⊂平面BB₁D₁D,所以B₁D⊥AC.同理可证B₁D⊥AD₁.又因为AC⊂平面ACD₁,AD₁⊂平面ACD₁,AC∩AD₁=A,所以B₁D⊥平面ACD₁.又因为B₁D⊂平面PDB₁,所以平面PDB₁⊥平面ACD₁,故④正确.
易错警示
本题易忽视点P在BC₁上运动时,平面PDB₁内的B₁D⊥平面ACD₁,导致无法证明平面PDB₁⊥平面
ACD₁而漏填④.
一条直线与一个平面垂直,则这条直线垂直于该平面内的任意一条直线.线线垂直、线面垂直和面面垂直之间是可以相互转化的,应准确掌握,灵活应用.
6.①②④【解析】如图1,连接AC,A₁C₁,A₁B,A₁P,
AD₁,D₁C.因为AA₁//CC₁,AA₁=CC₁,所以四边形
AA₁C₁C是平行四边形,所以AC//A₁C₁.又因为AC⊄平面A₁BC,A₁C₁⊂平面A₁BC,所以AC//平面
A₁BC.同理可证AD₁//平面A₁BC,又因为AC⊂平面
ACD₁,AD₁⊂平面ACD₁,且AC∩AD₁=A,所以平面
ACD₁//平面A₁BC.因为A₁P⊂平面A₁BC,所以A₁P//平面ACD₁,故②正确.因为BC//AD₁,所以BC//平面
ACD₁,所以点P到平面ACD₁的距离不变;又因为V三棱锥A₁−D₁PC=V三棱锥P−ACD₁,所以三棱锥A₁−D₁PC的体积不变,故①正确.


如图2,连接DB₁,DC₁,DP.因为DB₁=DC₁,所以当P为
BC₁的中点时才有DP⊥BC₁,故③错误.因为
BB₁⊥平面ABCD,AC⊂平面ABCD,所以AC⊥BB₁.又因为
AC⊥BD,BB₁∩BD=B,所以AC⊥平面BB₁D₁D.连接B₁D.因为B₁D⊂平面BB₁D₁D,所以B₁D⊥AC.同理可证B₁D⊥AD₁.又因为AC⊂平面ACD₁,AD₁⊂平面ACD₁,AC∩AD₁=A,所以B₁D⊥平面ACD₁.又因为B₁D⊂平面PDB₁,所以平面PDB₁⊥平面ACD₁,故④正确.
易错警示
本题易忽视点P在BC₁上运动时,平面PDB₁内的B₁D⊥平面ACD₁,导致无法证明平面PDB₁⊥平面
ACD₁而漏填④.
一条直线与一个平面垂直,则这条直线垂直于该平面内的任意一条直线.线线垂直、线面垂直和面面垂直之间是可以相互转化的,应准确掌握,灵活应用.
7. [2024·南宁一中月考]如图,二面角α-l-β的大小是60°,线段AB⊂α,B∈l,AB与l所成的角为30°,则AB与平面β所成的角的正弦值是
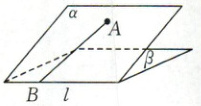
$\frac{\sqrt{3}}{4}$
。
答案:
7.$\frac{\sqrt{3}}{4}$【解析】如图,作AO⊥β于点
O,作AC⊥l于点C,连接OB,
 OC,则OC⊥l.设AB与β所成的
OC,则OC⊥l.设AB与β所成的
角为θ,则∠ABO=θ.由图得
sinθ=$\frac{AO}{AB}$=$\frac{AC}{AB}$·$\frac{AO}{AC}$=sin30°·sin60°=$\frac{\sqrt{3}}{4}$.
易错警示
对于异面直线所成角、线面角、二面角等空间角问题,一定要紧扣概念,注意角度的范围并能正确作出空间角.
7.$\frac{\sqrt{3}}{4}$【解析】如图,作AO⊥β于点
O,作AC⊥l于点C,连接OB,
 OC,则OC⊥l.设AB与β所成的
OC,则OC⊥l.设AB与β所成的角为θ,则∠ABO=θ.由图得
sinθ=$\frac{AO}{AB}$=$\frac{AC}{AB}$·$\frac{AO}{AC}$=sin30°·sin60°=$\frac{\sqrt{3}}{4}$.
易错警示
对于异面直线所成角、线面角、二面角等空间角问题,一定要紧扣概念,注意角度的范围并能正确作出空间角.
8. [2024·重庆八中月考]正三棱柱ABC-A₁B₁C₁的所有棱长都相等,则异面直线AB₁与BC₁所成的角的余弦值是
$\frac{1}{4}$
。
答案:
8.$\frac{1}{4}$【解析】设该三棱柱的棱长为2,
如图,取AB,BB₁,B₁C₁,BC的中点
 分别为L,M,N,P,连接LM,MN,
分别为L,M,N,P,连接LM,MN,
LN,则AB₁//LM,BC₁//MN,设直
线AB₁与BC₁所成的角为α,
则cosα=|cos∠LMN|,
连接LP,PN,易知NP⊥LP,LP=1,NP=2,
所以LN=√5.易知LB=BM=1,∠LBM=90°,
所以LM=√2,同理MN=$\sqrt{2}$.
在△LMN中,由余弦定理的推论得cos∠LMN=
$\frac{2+2-5}{2×\sqrt{2}×\sqrt{2}}$=−$\frac{1}{4}$,所以cosα=|cos∠LMN|=$\frac{1}{4}$.
易错警示
异面直线所成的角的范围是(0,$\frac{π}{2}$],在利用余弦定理求异面直线所成的角时,若出现角的余弦值为负值,不可错误地得出异面直线所成的角为钝角,此时应转化为正值求出相应的锐角.
8.$\frac{1}{4}$【解析】设该三棱柱的棱长为2,
如图,取AB,BB₁,B₁C₁,BC的中点
 分别为L,M,N,P,连接LM,MN,
分别为L,M,N,P,连接LM,MN,LN,则AB₁//LM,BC₁//MN,设直
线AB₁与BC₁所成的角为α,
则cosα=|cos∠LMN|,
连接LP,PN,易知NP⊥LP,LP=1,NP=2,
所以LN=√5.易知LB=BM=1,∠LBM=90°,
所以LM=√2,同理MN=$\sqrt{2}$.
在△LMN中,由余弦定理的推论得cos∠LMN=
$\frac{2+2-5}{2×\sqrt{2}×\sqrt{2}}$=−$\frac{1}{4}$,所以cosα=|cos∠LMN|=$\frac{1}{4}$.
易错警示
异面直线所成的角的范围是(0,$\frac{π}{2}$],在利用余弦定理求异面直线所成的角时,若出现角的余弦值为负值,不可错误地得出异面直线所成的角为钝角,此时应转化为正值求出相应的锐角.
查看更多完整答案,请扫码查看


