《2025年热搜题高中数学必修第二册人教版》

9. [2024·珠海一中月考]在△ABC 中，内角 A，B，C 的对边分别是 a，b，c. 若 a² + b² - mc² = 0(m 为常数)，且 $\frac{\cos A}{\sin A}$ + $\frac{\cos B}{\sin B}$ = $\frac{\cos C}{\sin C}$，则 m 的值为3.

答案： 9.3【解析】由余弦定理得$a^{2}+b^{2}=mc^{2}$，因为$a^{2}+b^{2}=c^{2}+2ab\cos C$，所以$c^{2}+2ab\cos C=mc^{2}$，即$2ab\cos C=(m - 1)c^{2}$.结合正弦定理得$2\sin A\sin B\cos C=(m - 1)\sin^{2}C$.由$\frac{\cos A}{\sin A}+\frac{\cos B}{\sin B}=\frac{\cos C}{\sin C}$，得$\sin A\sin B\cos C=\sin^{2}C$，所以$m - 1=2$，即$m=3$。

10. [2024·河北正定中学期中]如图，在△ABC 中，已知∠BAC = 120°，AB = 2，AC = 4，点 D 在 BC 上，且 BD = 2DC，E 是 AC 的中点，连接 AD，BE 相交于 O 点.
（1）求线段 AD，BE 的长；
（2）求∠EOD 的余弦值.

答案： 10.
(1)由题意得$\overrightarrow{BE}=\overrightarrow{AE}-\overrightarrow{AB}=\frac{1}{2}\overrightarrow{AC}-\overrightarrow{AB}$，所以$|\overrightarrow{BE}|^{2}=\overrightarrow{BE}^{2}=(\frac{1}{2}\overrightarrow{AC}-\overrightarrow{AB})^{2}=\frac{1}{4}\overrightarrow{AC}^{2}-\overrightarrow{AC}·\overrightarrow{AB}+\overrightarrow{AB}^{2}=\frac{1}{4}|\overrightarrow{AC}|^{2}-|\overrightarrow{AC}|·|\overrightarrow{AB}|·\cos\angle BAC+|\overrightarrow{AB}|^{2}=12$，所以$|\overrightarrow{BE}|=2\sqrt{3}$，即$BE=2\sqrt{3}$.因为$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AB}+\frac{2}{3}\overrightarrow{BC}=\overrightarrow{AB}+\frac{2}{3}(\overrightarrow{AC}-\overrightarrow{AB})=\frac{2}{3}\overrightarrow{AC}+\frac{1}{3}\overrightarrow{AB}$，所以$|\overrightarrow{AD}|^{2}=\overrightarrow{AD}^{2}=(\frac{2}{3}\overrightarrow{AC}+\frac{1}{3}\overrightarrow{AB})^{2}=\frac{4}{9}\overrightarrow{AC}^{2}+\frac{4}{9}\overrightarrow{AC}·\overrightarrow{AB}+\frac{1}{9}\overrightarrow{AB}^{2}=\frac{4}{9}|\overrightarrow{AC}|^{2}+\frac{4}{9}|\overrightarrow{AC}|·|\overrightarrow{AB}|\cos\angle BAC+\frac{1}{9}|\overrightarrow{AB}|^{2}=\frac{52}{9}$，所以$|\overrightarrow{AD}|=\frac{2\sqrt{13}}{3}$，即$AD=\frac{2\sqrt{13}}{3}$。
(2)因为$\overrightarrow{AD}=\frac{2}{3}\overrightarrow{AC}+\frac{1}{3}\overrightarrow{AB}$，$\overrightarrow{BE}=\frac{1}{2}\overrightarrow{AC}-\overrightarrow{AB}$，所以$\overrightarrow{AD}·\overrightarrow{BE}=(\frac{2}{3}\overrightarrow{AC}+\frac{1}{3}\overrightarrow{AB})(\frac{1}{2}\overrightarrow{AC}-\overrightarrow{AB})=\frac{1}{3}\overrightarrow{AC}^{2}-\frac{1}{2}\overrightarrow{AC}·\overrightarrow{AB}-\frac{1}{3}\overrightarrow{AB}^{2}=\frac{1}{3}×4^{2}-\frac{1}{2}×(-4)-\frac{1}{3}×2^{2}=6$，所以$\cos\angle EOD=\frac{\overrightarrow{AD}·\overrightarrow{BE}}{|\overrightarrow{AD}||\overrightarrow{BE}|}=\frac{6}{\frac{2\sqrt{13}}{3}×2\sqrt{3}}=\frac{3\sqrt{39}}{26}$。

11. 设△ABC 的内角 A，B，C 所对的边分别为 a，b，c，且 a cos C - $\frac{1}{2}$c = b.
（1）求角 A 的大小；
（2）若 a = 3，求△ABC 的周长的取值范围.

答案： 11.
(1)由$a\cos C-\frac{1}{2}c=b$及正弦定理，得$\sin A\cos C-\frac{1}{2}\sin C=\sin B$.因为$A + B + C=\pi$，所以$\sin B=\sin(\pi - A - C)=\sin A\cos C+\cos A\sin C$，所以$\frac{1}{2}\sin C=-\cos A\sin C$.因为$C\in(0,\pi)$，所以$\sin C\neq0$，所以$\cos A=-\frac{1}{2}$.又因为$A\in(0,\pi)$，所以$A=\frac{2\pi}{3}$.
(2)由正弦定理得$b=\frac{a\sin B}{\sin A}=2\sqrt{3}\sin B$，$c=\frac{a\sin C}{\sin A}=2\sqrt{3}\sin C$，所以$a + b + c=3 + 2\sqrt{3}(\sin B+\sin C)=3 + 2\sqrt{3}[\sin B+\sin(\frac{2\pi}{3}+B)]=3 + 2\sqrt{3}(\frac{3}{2}\sin B+\frac{\sqrt{3}}{2}\cos B)=3 + 3\sqrt{3}\sin(B+\frac{\pi}{3})$.因为$A=\frac{2\pi}{3}$，所以$B\in(0,\frac{\pi}{3})$，$B+\frac{\pi}{3}\in(\frac{\pi}{3},\frac{2\pi}{3})$，所以$\sin(B+\frac{\pi}{3})\in(\frac{\sqrt{3}}{2},1]$，所以$\triangle ABC$的周长的取值范围为$(6,3 + 2\sqrt{3}]$。

12. [2024·南宁一中月考]如图，在 O 处有一港口，两艘海轮 B，C 同时从港口 O 处出发向正北方向匀速航行，海轮 B 的航行速度为 20 海里/时，海轮 C 的航行速度大于海轮 B 的航行速度. 在港口 O 北偏东 60°方向上的 A 处有一观测站，1 小时后在 A 处测得与海轮 B 的距离为 30 海里，且 A 处对两艘海轮 B，C 的视角为 30°.
（1）求观测站 A 到港口 O 的距离；
（2）求海轮 C 的航行速度.

答案： 12.
(1)由题意知$OB = 20$海里.因为$AB = 30$海里，$\angle AOB = 60^{\circ}$，所以在$\triangle AOB$中，由余弦定理知$AB^{2}=OA^{2}+OB^{2}-2× OA× OB×\cos\angle AOB$，即$30^{2}=OA^{2}+20^{2}-2× OA×20×\cos60^{\circ}$，即$OA^{2}-20· OA - 500=0$，解得$OA=(10 + 10\sqrt{6})$（海里）（负值舍去）。所以观测站A到港口O的距离为$(10 + 10\sqrt{6})$海里.
(2)在$\triangle AOB$中，由正弦定理知$\frac{OB}{\sin\angle OAB}=\frac{AB}{\sin\angle AOB}$，即$\frac{20}{\sin\angle OAB}=\frac{30}{\sin60^{\circ}}$，解得$\sin\angle OAB=\frac{\sqrt{3}}{3}$.在$\triangle ABC$中，$\angle BAC = 30^{\circ}$，$\angle ABC = 60^{\circ}+\angle OAB$，所以$\angle ACB=90^{\circ}-\angle OAB$，所以$\sin\angle ACB=\sin(90^{\circ}-\angle OAB)=\cos\angle OAB=\sqrt{1-\sin^{2}\angle OAB}=\frac{\sqrt{6}}{3}$.在$\triangle ABC$中，由正弦定理知$\frac{BC}{\sin\angle BAC}=\frac{AB}{\sin\angle ACB}$，即$\frac{BC}{\frac{1}{2}}=\frac{30}{\frac{\sqrt{6}}{3}}$，解得$BC=\frac{15\sqrt{6}}{2}$（海里）.所以$OC=OB + BC=20+\frac{15\sqrt{6}}{2}$（海里）.所以海轮C的航行速度为$(20+\frac{15\sqrt{6}}{2})$海里/时.

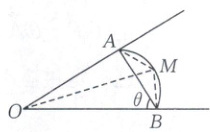
13. [2024·无锡一中期中]如图，某地修建了一座避暑山庄 O，为吸引游客，准备在门前两条夹角为 $\frac{\pi}{6}$（即∠AOB）的小路之间修建一处弓形花园. 已知弓形花园的弦长 AB = 2√3，且点 A，B 落在小路上，记弓形花园的顶点为 M，且∠MAB = ∠MBA = $\frac{\pi}{6}$，设∠OBA = θ.
（1）将 OA，OB 用含 θ 的式子表示出来；
（2）该山庄准备在 M 点处修建喷泉，如何规划花园（即 OA，OB 的长度），才能使喷泉 M 与山庄 O 的距离（即 OM 的长度）最大？

答案： 13.
(1)在$\triangle ABO$中，由正弦定理得$\frac{OA}{\sin\theta}=\frac{OB}{\sin\angle OAB}=\frac{AB}{\sin\frac{\pi}{6}}$，又$AB = 2\sqrt{3}$，$\angle OAB=\frac{5\pi}{6}-\theta$，所以$OA = 4\sqrt{3}\sin\theta$，$OB = 4\sqrt{3}\sin(\frac{5\pi}{6}-\theta)=4\sqrt{3}\sin(\theta+\frac{\pi}{6})$，$\theta\in(0,\frac{5\pi}{6})$.
(2)因为$AB = 2\sqrt{3}$，$\angle MAB=\angle MBA=\frac{\pi}{6}$，所以$AM = BM = 2$.在$\triangle OMB$中，由余弦定理得$OM^{2}-OB^{2}+BM^{2}-2OB· BM·\cos(\theta+\frac{\pi}{6})=48\sin^{2}(\theta+\frac{\pi}{6})+4 - 16\sqrt{3}\sin(\theta+\frac{\pi}{6})\cos(\theta+\frac{\pi}{6})=-24[1-\cos(\frac{\pi}{3}+2\theta)]+4 - 8\sqrt{3}\sin(\frac{\pi}{3}+2\theta)=-16\sqrt{3}[\frac{1}{2}\sin(\frac{\pi}{3}+2\theta)+\frac{\sqrt{3}}{2}\cos(\frac{\pi}{3}+2\theta)]+28=-16\sqrt{3}\sin(2\theta+\frac{2\pi}{3})+28$.由
(1)得$\theta\in(0,\frac{5\pi}{6})$，所以$2\theta+\frac{2\pi}{3}\in(\frac{2\pi}{3},\frac{7\pi}{3})$，所以$\sin(2\theta+\frac{2\pi}{3})\in[-1,\frac{\sqrt{3}}{2})$，所以当$\sin(2\theta+\frac{2\pi}{3})=-1$，即$\theta=\frac{5\pi}{12}$时，$OM$的长度取得最大值，为$\sqrt{28 + 16\sqrt{3}}=4 + 2\sqrt{3}$，此时$OA = 4\sqrt{3}\sin\frac{5\pi}{12}=4\sqrt{3}(\sin\frac{\pi}{4}\cos\frac{\pi}{6}+\cos\frac{\pi}{4}\sin\frac{\pi}{6})=\sqrt{6}+3\sqrt{2}$，$OB = 4\sqrt{3}\sin(\frac{5\pi}{12}+\frac{\pi}{6})=4\sqrt{3}\sin(\pi-\frac{5\pi}{12})=4\sqrt{3}\sin\frac{5\pi}{12}=\sqrt{6}+3\sqrt{2}$，故当$OA = OB=\sqrt{6}+3\sqrt{2}$时，$OM$的长度取得最大值，即喷泉M与山庄O的距离最大.