《2025年热搜题高中数学必修第二册人教版》

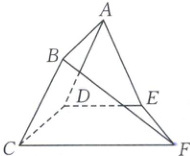
5. [2024·天津模拟]如图，矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角，DE//CF，CD⊥DE，AD = 2，EF = $3\sqrt{2}$，CF = 6，∠CFE = 45°.
(1)求证:平面CDEF⊥平面BCF.
(2)试问在线段CF上是否存在一点G，使锐二面角B - EG - D的余弦值为$\frac{1}{4}$?若存在，求出CG的值;若不存在，请说明理由.

答案：

(1)证明：因为四边形ABCD是矩形，所以CD⊥BC.因为CD⊥DE，DE//CF，所以CD⊥CF.
又因为BC∩CF = C，BC，CF⊂平面BCF，所以CD⊥平面BCF.
又因为CD⊂平面CDEF，所以平面CDEF⊥平面BCF.
(2)存在，当CG = $\frac{3}{2}$时，符合题意.理由如下：
由
(1)得平面CDEF⊥平面BCF，在平面BCF内，作BO⊥CF于点O，如图.
因为平面CDEF∩平面BCF = CF，BO⊂平面BCF，所以BO⊥平面CDEF.
过点O作OH⊥EH，垂足为H，EH交CF于点G，连接BH.
因为HO为HB在平面CDEF内的射影，所以∠BHO是锐二面角B - EG - D的平面角.
又因为锐二面角B - EG - D的余弦值是$\frac{1}{4}$，所以cos∠BHO = $\frac{1}{4}$.
易得∠BCF为锐二面角A - CD - F的平面角，所以∠BCF = 60°.
又因为BC = AD = 2，所以BO = √3，CO = 1.
所以OH = $\frac{\sqrt{5}}{5}$.
取CF的中点M，连接EM.
因为CF = 6，所以MF = CM = 3，所以OM = 2.
又EF = 3√2，∠CFE = 45°，所以由余弦定理可得EM = 3，所以EM² + MF² = EF²，所以EM⊥CF.
设OG = x(x ＞ 0)，易得△OHG与△EMG相似，则$\frac{OH}{OG}$ = $\frac{EM}{EG}$，即$\frac{\frac{\sqrt{5}}{5}}{x}$ = $\frac{3}{\sqrt{9+(2 - x)^{2}}}$，解得x = $\frac{1}{2}$或x = -$\frac{13}{22}$(舍去)，所以OG = $\frac{1}{2}$，此时CG = $\frac{3}{2}$.
所以存在符合题意的点G，且CG = $\frac{3}{2}$.

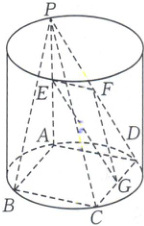
6. [2024·广州调考]如图，圆柱的高为2，A，B，C，D分别是圆柱下底面圆周上的点，四边形ABCD为矩形，PA是圆柱的母线，AB = 2，BC = 4，E，F，G分别是线段PA，PD，CD的中点.
(1)求证:平面PDC⊥平面PAD.
(2)求证:PB//平面EFG.
(3)在线段BC上是否存在一点M，使得点D到平面PAM的距离为2?若存在，求出BM;若不存在，请说明理由.

答案：

(1)证明：因为PA是圆柱的母线，所以PA⊥圆柱的底面.
因为CD⊂圆柱的底面，所以PA⊥CD.
又因为四边形ABCD为矩形，所以CD⊥AD.
又PA∩AD = A，PA，AD⊂平面PAD，所以CD⊥平面PAD.
又CD⊂平面PDC，所以平面PDC⊥平面PAD.
(2)证明：如图，取AB的中点H，连接GH，HE.
因为E，F，G分别是线段PA，PD，CD的中点，所以GH//AD//EF，所以E，F，G，H四点共面.
又H为AB的中点，所以EH//PB.
又EH⊂平面EFG，PB⊄平面EFG，所以PB//平面EFG.
(3)如图，假设在BC上存在一点M，使得D到平面PAM的距离为2，则以△PAM为底，D为顶点的三棱锥的高为2，连接DM，则AM = $\sqrt{AB^{2}+BM^{2}}$ = $\sqrt{4+BM^{2}}$.
由
(1)知PA⊥AM，所以S_{△PAM} = $\frac{1}{2}$PA·AM = $\frac{1}{2}$×2×$\sqrt{4+BM^{2}}$ = $\sqrt{4+BM^{2}}$.
所以V_{三棱锥D - PAM} = $\frac{1}{3}$S_{△PAM}·2 = $\frac{2}{3}$$\sqrt{4+BM^{2}}$.
因为S_{△ADM} = $\frac{1}{2}$AD·AB = $\frac{1}{2}$×4×2 = 4，所以V_{三棱锥P - ADM} = $\frac{1}{3}$S_{ADM}·PA = $\frac{1}{3}$×4×2 = $\frac{8}{3}$.
因为V_{三棱锥D - PAM} = V_{P - ADM}，所以$\frac{2}{3}$$\sqrt{4+BM^{2}}$ = $\frac{8}{3}$，解得BM = 2√3.
因为2√3 ＜ 4，所以线段BC上存在一点M，当BM = 2√3时，使得D到平面PAM的距离为2.

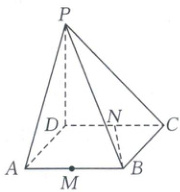
7. [2024·江苏镇江中学月考]如图，在四棱锥P - ABCD中，底面ABCD是边长为2的菱形，∠BAD = 60°，PD⊥底面ABCD，PD = AD，M，N分别是棱AB，CD的中点.
(1)证明:BN⊥平面PCD.
(2)在线段PC上是否存在点H，使得MH与平面PCD所成最大角的正切值为$\frac{\sqrt{6}}{2}$?若存在，请求出H点的位置;若不存在，请说明理由.

答案：

(1)证明：如图，连接BD，在菱形ABCD中，∠BAD = 60°，则△BCD为等边三角形.
因为N是CD的中点，所以BN⊥CD.
又PD⊥底面ABCD，且BN⊂底面ABCD，所以PD⊥BN.
又PD∩CD = D，PD，CD⊂平面PCD，所以BN⊥平面PCD.
(2)存在.理由如下：
假设线段PC上存在点H满足题意.
连接DH，DM，易得DN//BM，且DN = BM，所以四边形BMDN为平行四边形，所以DM//BN.
由
(1)可知，BN⊥平面PCD，所以DM⊥平面PCD.
又DH⊂平面PCD，所以DM⊥DH，所以∠MHD即为MH与平面PCD所成的角.
由题意得，当DH最小时，即DH⊥PC时，∠MHD最大，此时tan∠MHD = $\frac{DM}{DH}$ = $\frac{\sqrt{6}}{2}$.
又DM = $\frac{\sqrt{3}}{2}$AD = √3，所以DH = √2.
在Rt△DHC中，DH = √2，CD = 2，所以CH = $\sqrt{CD^{2}-DH^{2}}$ = √2.
所以线段PC上存在点H，当CH = √2时，MH与平面PCD所成最大角的正切值为$\frac{\sqrt{6}}{2}$.

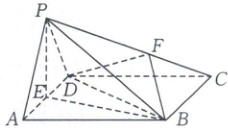
8. [2024·三明一中期末]如图，在四棱锥P - ABCD中，底面ABCD是菱形，∠BAD = 60°，△PAD是正三角形，E为线段AD的中点，$\overrightarrow{PF}$ = $\lambda\overrightarrow{FC}$($\lambda$ ＞ 0).
(1)求证:平面PBC⊥平面PBE.
(2)是否存在点F，使得$V_{三棱锥B - PAE}$ = $\frac{5}{8}V_{三棱锥D - PFB}$?若存在，求出$\lambda$的值;若不存在，请说明理由.
(3)若平面PAD⊥平面ABCD，在平面PBE内确定一点H，使CH + FH的值最小，并求此时$\frac{BH}{PB}$的值.

答案：

(1)证明：因为△PAD是正三角形，E为线段AD的中点，所以PE⊥AD.
因为四边形ABCD是菱形，所以AD = AB.
因为∠BAD = 60°，所以△ABD是正三角形，所以BE⊥AD.
又BE∩PE = E，BE，PE⊂平面PBE，所以AD⊥平面PBE.
又AD//BC，所以BC⊥平面PBE.
因为BC⊂平面PBC，所以平面PBC⊥平面PBE.
(2)存在点F，使得V_{三棱锥B - PAE} = $\frac{5}{8}$V_{三棱锥D - PFB}.理由如下：
由$\overrightarrow{PF}$ = λ$\overrightarrow{FC}$，知PC = $\overrightarrow{PF}$ + $\overrightarrow{FC}$ = (λ + 1)$\overrightarrow{FC}$，所以V_{三棱锥B - PAE} = $\frac{1}{2}$V_{三棱锥B - PAD} = $\frac{1}{2}$V_{三棱锥P - ADB} = $\frac{1}{2}$V_{三棱锥P - BCD} = $\frac{λ + 1}{2}$V_{三棱锥F - BCD}.
V_{三棱锥D - PFB} = V_{三棱锥P - BDC} - V_{三棱锥F - BCD} = λV_{三棱锥F - BCD}.
又V_{三棱锥B - PAE} = $\frac{5}{8}$V_{三棱锥D - PFB}，所以$\frac{λ + 1}{2}$ = $\frac{5λ}{8}$，解得λ = 4.
即存在满足$\overrightarrow{PF}$ = λ$\overrightarrow{FC}$(λ ＞ 0)的点F，使得V_{三棱锥B - PAE} = $\frac{5}{8}$V_{三棱锥D - PFB}，此时λ = 4.
(3)如图，延长CB到C′，使得BC′ = CB，由
(1)知CB⊥平面PBE.
因为PB⊂平面PBE，所以CB⊥PB，则C′是点C关于面PBE的对称点.
在平面PBC中，过点C′作C′F⊥PC，垂足为F，交PB于点H，此时CH + FH的值最小.
设BC = 2a，则PE = BE = √3a.
因为平面PAD⊥平面ABCD，平面PAD∩平面ABCD = AD，PE⊥AD，PE⊂平面PAD，所以PE⊥平面ABCD.
因为BE⊂平面ABCD，所以PE⊥BE，所以PB = $\sqrt{6}$a.
所以tan∠BC′H = tan∠BPC = $\frac{BC}{PB}$ = $\frac{\sqrt{6}}{3}$，所以BH = BC′tan∠BC′H = $\frac{2\sqrt{6}}{3}$a，所以$\frac{BH}{PB}$ = $\frac{2}{3}$.