《2025年热搜题高中数学必修第二册人教版》

1. [2024·烟台一中期末]下列等式恒成立的是(D)

A.$\overrightarrow{AB}+\overrightarrow{BA}=0$
B.$\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{BC}$
C.$(\boldsymbol{a}·\boldsymbol{b})·\boldsymbol{c}=\boldsymbol{a}·(\boldsymbol{b}·\boldsymbol{c})$
D.$(\boldsymbol{a}+\boldsymbol{b})·\boldsymbol{c}=\boldsymbol{a}·\boldsymbol{c}+\boldsymbol{b}·\boldsymbol{c}$

答案： 1.D[解析] $\overrightarrow{AB}+\overrightarrow{BA}=0$，故A错误；$\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}$，故B错误；$(a· b)· c$表示与c共线的向量，而$a·(b· c)$表示与a共线的向量，故C错误；根据平面向量数量积的运算性质可知D正确。故选D。

2. [2024·绵阳二中期中]已知向量 $\boldsymbol{a}=(1,2)$，$\boldsymbol{b}=(2,-3)$. 若向量 $\boldsymbol{c}$ 满足 $(\boldsymbol{c}+\boldsymbol{a})//\boldsymbol{b}$，$\boldsymbol{c}\perp(\boldsymbol{a}+\boldsymbol{b})$，则 $\boldsymbol{c}=$(D)

A.$(\frac{7}{9},\frac{7}{3})$
B.$(-\frac{7}{3},-\frac{7}{9})$
C.$(\frac{7}{3},\frac{7}{9})$
D.$(-\frac{7}{9},-\frac{7}{3})$

答案： 2.D[解析]设$c=(x,y)$，由$(c + a)// b$得$-3(x + 1) - 2(y + 2) = 0$。
由$c\perp(a + b)$得$3x - y = 0$。
联立$\begin{cases}-3(x + 1) - 2(y + 2) = 0\\3x - y = 0\end{cases}$得$x = -\frac{7}{9},y = -\frac{7}{3}$，
则$c = (-\frac{7}{9},-\frac{7}{3})$。故选D。

3. [2024·江西临川一中月考]在直角梯形 $ABCD$ 中，$AB// CD$，$AD\perp AB$，$B = 45^{\circ}$，$AB = 2CD = 2$，$M$ 为腰 $BC$ 的中点，则 $\overrightarrow{MA}·\overrightarrow{MD}=$(B)

A.1
B.2
C.3
D.4

答案： 3.B[解析]由已知得$BC = \sqrt{2},\angle BCD = 135^{\circ}$，所以$\overrightarrow{MA}·\overrightarrow{MD}=(\overrightarrow{MB}+\overrightarrow{BA})·(\overrightarrow{MC}+\overrightarrow{CD})=\overrightarrow{MB}·\overrightarrow{MC}+\overrightarrow{MB}·\overrightarrow{CD}+\overrightarrow{BA}·\overrightarrow{MC}+\overrightarrow{BA}·\overrightarrow{CD}=\frac{\sqrt{2}}{2}×\frac{\sqrt{2}}{2}×\cos180^{\circ}+\frac{\sqrt{2}}{2}×1×\cos135^{\circ}+2×\frac{\sqrt{2}}{2}×\cos45^{\circ}+2×1×\cos0^{\circ}=2$。

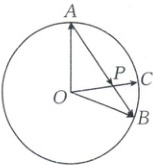
4. [2024·西安一中期末]如图，$A$，$B$，$C$ 是圆 $O$ 上不重合的三点，线段 $OC$ 与线段 $AB$ 交于圆内一点 $P$. 若 $\overrightarrow{OC}=m\overrightarrow{OA}+2m\overrightarrow{OB}$，$\overrightarrow{AP}=\lambda\overrightarrow{AB}$，则 $\lambda=$(D)


A.$\frac{5}{6}$
B.$\frac{4}{5}$
C.$\frac{3}{4}$
D.$\frac{2}{3}$

答案： 4.D[解析]由题意，设$\overrightarrow{OP}=n\overrightarrow{OC}$。因为$\overrightarrow{AP}=\lambda\overrightarrow{AB}$，所以$\overrightarrow{OP}-\overrightarrow{OA}=\lambda(\overrightarrow{OB}-\overrightarrow{OA})$，故$n\overrightarrow{OC}-\overrightarrow{OA}=\lambda(\overrightarrow{OB}-\overrightarrow{OA})$，
所以$n(m\overrightarrow{OA}+2m\overrightarrow{OB})-\overrightarrow{OA}=\lambda(\overrightarrow{OB}-\overrightarrow{OA})$，即$(mn+\lambda - 1)\overrightarrow{OA}+(2mn-\lambda)\overrightarrow{OB}=0$。而$\overrightarrow{OA}$与$\overrightarrow{OB}$不共线，故有$\begin{cases}mn+\lambda - 1=0\\2mn-\lambda=0\end{cases}$，解得$\lambda=\frac{2}{3}$。故选D。

5. [2024·招远一中月考]已知向量 $\boldsymbol{a}=(3,2)$，$\boldsymbol{b}=(-1,m+\frac{7}{2})$，且函数 $f(x)=(\boldsymbol{a}+x\boldsymbol{b})·(x\boldsymbol{a}-\boldsymbol{b})$ 的图象是一条直线，则 $|\boldsymbol{b}|=$(A)

A.$\frac{\sqrt{13}}{2}$
B.$\sqrt{14}$
C.$2\sqrt{7}$
D.$2\sqrt{10}$

答案： 5.A[解析]$f(x)=(a + xb)·(xa - b)=x|a|^2 - a· b + x^2a· b - x|b|^2$，因为函数$f(x)$的图象是一条直线，所以$a· b = 0$，且$|a|^2\neq|b|^2$，所以$3×(-1)+2×(m+\frac{7}{2})=0$且$3^2+2^2\neq(-1)^2+(m+\frac{7}{2})^2$，解得$m = -2$，
所以$b = (-1,\frac{3}{2})$，$|b|=\sqrt{(-1)^2+(\frac{3}{2})^2}=\frac{\sqrt{13}}{2}$。

6. [2024·石家庄二中期中]在一条东西走向的水平公路的北侧远处有一座高塔，塔底与这条公路在同一水平面上. 为测量该塔的高度，测量人员在公路上选择了 $A$，$B$ 两个观测点，在 $A$ 处测得该塔底部 $C$ 在西偏北 $\alpha$ 的方向上，在 $B$ 处测得该塔底部 $C$ 在西偏北 $\beta$ 的方向上，并测得塔顶 $D$ 的仰角为 $\gamma$. 已知 $AB = a$，$0\lt\gamma\lt\beta\lt\alpha\lt\frac{\pi}{2}$，则此塔的高 $CD$ 为(B)

A.$\frac{a\sin(\alpha-\beta)}{\sin\alpha}\tan\gamma$
B.$\frac{a\sin\alpha}{\sin(\alpha-\beta)}\tan\gamma$
C.$\frac{a\sin(\alpha-\beta)\sin\beta}{\sin\alpha}\tan\gamma$
D.$\frac{a\sin\alpha\sin\beta}{\sin(\alpha-\beta)}\tan\gamma$

答案： 6.B[解析]依题意，得在$\triangle ABC$中，$AB = a$，$\angle CAB = \pi - \alpha$，$\angle ACB = \alpha - \beta$，由正弦定理得$\frac{AB}{\sin(\alpha - \beta)}=\frac{BC}{\sin(\pi - \alpha)}$，
所以$BC = \frac{a\sin\alpha}{\sin(\alpha - \beta)}$。在$\triangle BCD$中，$\angle CBD = \gamma$，$CD = BC\tan\gamma=\frac{a\sin\alpha}{\sin(\alpha - \beta)}·\tan\gamma$。故选B。

7. [2024·北师大附中期中]对于非零向量 $\boldsymbol{\alpha}$，$\boldsymbol{\beta}$，定义一种向量积：$\boldsymbol{\alpha}\circ\boldsymbol{\beta}=\frac{\boldsymbol{\alpha}·\boldsymbol{\beta}}{\boldsymbol{\beta}·\boldsymbol{\beta}}$. 已知非零向量 $\boldsymbol{a}$，$\boldsymbol{b}$ 的夹角 $\theta\in(\frac{\pi}{4},\frac{\pi}{2})$，且 $\boldsymbol{a}\circ\boldsymbol{b}$，$\boldsymbol{b}\circ\boldsymbol{a}$ 都在集合 $\{\frac{n}{2}|n\in\mathbf{N}\}$ 中，则 $\boldsymbol{a}\circ\boldsymbol{b}=$(D)

A.$\frac{5}{2}$ 或 $\frac{3}{2}$
B.$\frac{1}{2}$ 或 $\frac{3}{2}$
C.1
D.$\frac{1}{2}$

答案： 7.D[解析]$a\circ b=\frac{a· b}{b· b}=\frac{|a|·|b|\cos\theta}{|b|^2}=\frac{|a|\cos\theta}{|b|}=\frac{n}{2}$，$n\in N$，
同理可得$b\circ a=\frac{b· a}{a· a}=\frac{|a|·|b|\cos\theta}{|a|^2}=\frac{|b|\cos\theta}{|a|}=\frac{m}{2}$，$m\in N$。
再由a与b的夹角$\theta\in(\frac{\pi}{4},\frac{\pi}{2})$，可得$\cos^2\theta\in(0,\frac{1}{2})$，
①②两式相乘得$\cos^2\theta=\frac{mn}{4}$，$m,n\in N$，所以$m = n = 1$，所以$a\circ b=\frac{n}{2}=\frac{1}{2}$。故选D。

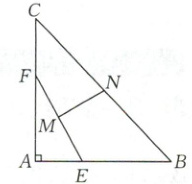
8. [2024·重庆八中月考]如图，在等腰直角三角形 $ABC$ 中，$AB = AC = 2$，$\angle BAC = 90^{\circ}$，$E$，$F$ 分别为 $AB$，$AC$ 上的动点，设 $\overrightarrow{AE}=\lambda\overrightarrow{AB}$，$\overrightarrow{AF}=\mu\overrightarrow{AC}$，其中 $\lambda$，$\mu\in(0,1)$，则下列说法不正确的是(B)


A.若 $|\overrightarrow{BE}|=|\overrightarrow{AF}|$，则 $\lambda+\mu = 1$
B.若 $\lambda=\mu$，则 $\overrightarrow{EF}$ 与 $\overrightarrow{BC}$ 不共线
C.若 $\lambda+\mu = 1$，则 $S_{\triangle AEF}$ 的最大值为 $\frac{1}{2}$
D.若 $\lambda^{2}+\mu^{2}=1$，且 $M$，$N$ 分别为 $EF$，$BC$ 的中点，则 $|MN|$ 的最小值为 $\sqrt{2}-1$

答案：
8.B[解析]对于A，因为$\overrightarrow{AE}=\lambda\overrightarrow{AB}$，$\overrightarrow{AF}=\mu\overrightarrow{AC}$，且$|\overrightarrow{BE}| = |\overrightarrow{AF}|$，所以$(1 - \lambda)|\overrightarrow{AB}| = \mu|\overrightarrow{AC}|$，所以$(1 - \lambda)^2 = \mu^2$，其中$\lambda,\mu\in(0,1)$，所以$1 - \lambda = \mu$，即$\lambda + \mu = 1$，所以A正确。对于B，当$\lambda = \mu$时，$\overrightarrow{EF}=\overrightarrow{AF}-\overrightarrow{AE}=\mu\overrightarrow{AC}-\lambda\overrightarrow{AB}=\mu(\overrightarrow{AC}-\overrightarrow{AB})=\mu\overrightarrow{BC}$，可得$\overrightarrow{EF}$与$\overrightarrow{BC}$为共线向量，所以B不正确。对于C，在等腰直角$\triangle ABC$中，$AB = AC = 2$，$\angle BAC = 90^{\circ}$，且$\overrightarrow{AE}=\lambda\overrightarrow{AB}$，$\overrightarrow{AF}=\mu\overrightarrow{AC}$，所以$S_{\triangle AEF}=\frac{1}{2}|\overrightarrow{AE}|·|\overrightarrow{AF}|=\frac{1}{2}|\lambda\overrightarrow{AB}|·|\mu\overrightarrow{AC}|=2\lambda\mu$，由$\lambda + \mu = 1$，可得$\lambda\mu\leq(\frac{\lambda + \mu}{2})^2=\frac{1}{4}$，所以$S_{\triangle AEF}=2\lambda\mu\leq\frac{1}{2}$，当且仅当$\lambda = \mu=\frac{1}{2}$时，等号成立，所以C正确。对于D，如图所示，以A为坐标原点，AB，AC分别为x轴、y轴建立平面直角坐标系，则$A(0,0)$，$B(2,0)$，$C(0,2)$，则$\overrightarrow{AE}=\lambda\overrightarrow{AB}=(2\lambda,0)$，$\overrightarrow{AF}=\mu\overrightarrow{AC}=(0,2\mu)$。因为M，N分别为EF，BC的中点，所以$M(\lambda,\mu)$，$N(1,1)$。又因为$\lambda^2+\mu^2=1$，$\lambda,\mu\in(0,1)$，可得点M在单位圆的劣弧PQ上，$|AM| = 1$，所以$|MN|\geq|AN|-|AM|=\sqrt{2}-1$，当且仅当A，M，N三点共线时，等号成立，所以$|MN|$的最小值为$\sqrt{2}-1$，所以D正确。