《2025年热搜题高中数学必修第二册人教版》

1. [2024·长沙长郡中学月考]若圆锥的轴截面是正三角形，则它的侧面积是底面积的(C)

A.$\sqrt{2}$倍
B.3 倍
C.2 倍
D.5 倍

答案：
1.C[解析]如图所示，设OC=r,则AC=2r.所以圆锥的底面积为S₁=πr²,圆锥的侧面积为S₂= $\frac{1}{2}$(2πr)·2r = 2πr², $\frac{S₂}{S₁}$ = $\frac{2πr²}{πr²}$ = 2,则圆锥的侧面积是底面积的2倍.故选C.

2. [2024·苏州中学月考]圆台的上、下底面半径和高的比为 $1:4:4$，母线长为 10，则圆台的侧面积为(B)

A.$81\pi$
B.$100\pi$
C.$14\pi$
D.$169\pi$

答案： 2.B[解析]因为圆台的上、下底面半径和高的比为1:4:4,母线长为10，设圆台上底面的半径为r，则下底面半径和高分别为4r和4r.由100 = (4r)² + (4r - r)²得r = 2.故圆台的侧面积为π(r + 4r)×10 = 100π.故选B.

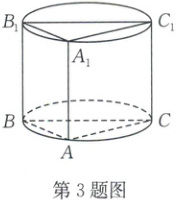
3. [2024·任丘一中月考](多选)如图，圆柱的轴截面是四边形 $BCC_1B_1$，$AA_1$ 是圆柱的一条母线，已知 $AB = 4$，$AC = 2\sqrt{2}$，$AA_1 = 3$，则下列说法正确的有(BC)

A.圆柱的侧面积为 $2\sqrt{3}\pi$
B.圆柱的侧面积为 $6\sqrt{6}\pi$
C.圆柱的表面积为 $6\sqrt{6}\pi + 12\pi$
D.圆柱的表面积为 $2\sqrt{6}\pi + 6\pi$

答案： 3.BC[解析]因为四边形BCC₁B₁是圆柱的轴截面，AA₁是圆柱的一条母线，AB = 4，AC = 2$\sqrt{2}$，AA₁ = 3，所以圆柱的底面半径r = $\frac{1}{2}$BC = $\frac{1}{2}$$\sqrt{4² + (2\sqrt{2})²}$ = $\sqrt{6}$，所以圆柱的侧面积S = 2πr×AA₁ = 6$\sqrt{6}$π，故A错误，B正确.圆柱的表面积S′ = S + 2S底面 = 6$\sqrt{6}$π + 2π×($\sqrt{6}$)² = 6$\sqrt{6}$π + 12π，故C正确，D错误.故选BC.

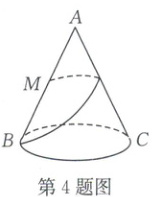
4. [2024·景德镇一中期末]如图，圆锥的母线长为 4，$M$ 为母线 $AB$ 的中点，从点 $M$ 处拉一条绳子，绕圆锥的侧面转一周到达点 $B$，这条绳子的最短长度为 $2\sqrt{5}$，则此圆锥的表面积为(B)

A.$4\pi$
B.$5\pi$
C.$6\pi$
D.$8\pi$

答案：
4.B[解析]将圆锥侧面展开成一个扇形，如图所示.设圆锥的底面半径为r，因为母线长为4，所以侧面展开扇形的圆心角α = $\frac{2πr}{4}$ = $\frac{πr}{2}$.易知B′M的长度即为绳子的最短长度，即B′M = 2$\sqrt{5}$.在△AB′M中，B′M = $\sqrt{4² + 2² - 2×4×2×cos\frac{πr}{2}}$ = $\sqrt{20 - 16cos\frac{πr}{2}}$ = 2$\sqrt{5}$，则cos$\frac{πr}{2}$ = 0，所以r = 1，所以圆锥的表面积S = π×1² + π×1×4 = 5π.故选B.

5. [2024·北师大实验中学单元检测]已知圆柱的侧面展开图是一个边长为 $2\pi$ 的正方形，则这个圆柱的体积是(A)

A.$2\pi^2$
B.$\pi^2$
C.$\frac{\pi^2}{2}$
D.$\frac{\pi^2}{3}$

答案： 5.A[解析]由底面圆周长l = 2π = 2πr，得r = 1，则S = πr² = π，所以V = Sh = π×2π = 2π².故选A.

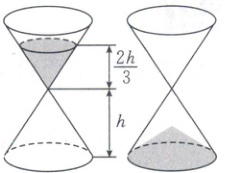
6. [2024·辽阳一中期末]中国古代计时器的发明时间不晚于战国时代，其中沙漏就是古代利用机械原理设计的一种计时装置，它根据细沙从一个容器漏到另一个容器的时间来计量时间.如图，某沙漏由上、下两个圆锥容器组成，圆锥的底面直径和高均为 $8$ cm，细沙全部在上部时，其高度为圆锥高度的 $\frac{2}{3}$(两圆锥连接处长度忽略不计).若细沙全部漏入下部后，恰好堆成一个盖住沙漏底部的圆锥形沙堆，则此圆锥形沙堆的高为(D)


A.$2$ cm
B.$\frac{4}{3}$ cm
C.$\frac{2}{3}$ cm
D.$\frac{64}{27}$ cm

答案： 6.D[解析]由题意可知，开始时，沙漏上部分圆锥中的细沙的高H = $\frac{2}{3}$×8 = $\frac{16}{3}$，底面半径r = $\frac{2}{3}$×4 = $\frac{8}{3}$，故细沙的体积V = $\frac{1}{3}$πr²H = $\frac{1}{3}$π×($\frac{8}{3}$)²×$\frac{16}{3}$ = $\frac{1024π}{81}$.当细沙漏入下部后，圆锥形沙堆的底面半径为4，设高为H′，则$\frac{1}{3}$π×4²×H′ = $\frac{1024π}{81}$，解得H′ = $\frac{64}{27}$.故此圆锥形沙堆的高为$\frac{64}{27}$cm.故选D.

7. [2024·宁波镇海中学月考]已知某圆台的上、下底面面积分别是 $\pi$，$4\pi$，侧面积是 $6\pi$，则这个圆台的体积是$\frac{7\sqrt{3}π}{3}$.

答案： 7.$\frac{7\sqrt{3}π}{3}$[解析]设圆台的上、下底面半径分别为r和R，母线长为l，高为h，则S上 = πr² = π，S下 = πR² = 4π，S侧 = π(r + R)l = 6π，所以r = 1，R = 2，l = 2，所以h = $\sqrt{l² - (R - r)²}$ = $\sqrt{3}$，所以V = $\frac{1}{3}$π(1 + 4 + 1×2)×$\sqrt{3}$ = $\frac{7\sqrt{3}π}{3}$.

8. [2024·邯郸一中周练]将一个圆形纸片沿半径剪开为两个扇形，其圆心角之比为 $3:4$，再将它们卷成两个圆锥侧面，则这两个圆锥的体积之比为$\frac{3\sqrt{330}}{88}$.

答案： 8.$\frac{3\sqrt{330}}{88}$[解析]设圆的半径为r，则两个圆锥的母线长为r.由已知可得两个圆锥的底面半径分别为$\frac{2πr×\frac{3}{7}}{2π}$ = $\frac{3}{7}$r，$\frac{2πr×\frac{4}{7}}{2π}$ = $\frac{4}{7}$r，所以两圆锥的体积之比为$\frac{\frac{1}{3}π×(\frac{3}{7}r)²×\sqrt{r² - (\frac{3}{7}r)²}}{\frac{1}{3}π×(\frac{4}{7}r)²×\sqrt{r² - (\frac{4}{7}r)²}}$ = $\frac{3\sqrt{330}}{88}$.

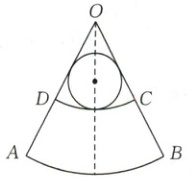
9. [2024·合肥一中月考]如图所示，有一块扇形铁皮 $OAB$，$\angle AOB = 60^{\circ}$，$OA = 72$ cm，要剪下来一个扇形环 $ABCD$，作圆台型容器的侧面，并且要在余下的扇形 $OCD$ 内剪下一块与其相切的圆，使它恰好作圆台型容器的下底面(大底面)，则 $AD$ 的长为36cm，容器的容积为504$\sqrt{35}$πcm³.

答案： 9.36cm 504$\sqrt{35}$πcm³[解析]设圆台上、下底面半径分别为r₁cm，r₂cm，AD = xcm，则OD = (72 - x)cm，由题意可得，$\frac{2πr₂}{180}$×72 = $\frac{60π}{180}$×72，所以$\begin{cases}r₂ = 12\\x = 36\end{cases}$，即AD的长为36cm.因为2πr₁ = $\frac{60π}{180}$·OD = 12π，所以r₁ = 6，圆台的高h = $\sqrt{x² - (r₂ - r₁)²}$ = $\sqrt{36² - (12 - 6)²}$ = 6$\sqrt{35}$(cm).所以V = $\frac{1}{3}$πh(r₂² + r₂r₁ + r₁²) = $\frac{1}{3}$π×6$\sqrt{35}$×(12² + 12×6 + 6²) = 504$\sqrt{35}$π(cm³).即容器的容积为504$\sqrt{35}$πcm³.