2025年热搜题高中数学必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年热搜题高中数学必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. [2024·重庆巴蜀中学月考]将一个棱长为a的正方体,切成27个全等的小正方体,则表面积增加了(
A.$6a^{2}$
B.$12a^{2}$
C.$18a^{2}$
D.$24a^{2}$
B
)A.$6a^{2}$
B.$12a^{2}$
C.$18a^{2}$
D.$24a^{2}$
答案:
1.B 【解析】原来正方体的表面积为$S_1 = 6a^2$,切割成27个全等的小正方体后,每个小正方体的棱长为$\frac{1}{3}a$,表面积为$6 × (\frac{1}{3}a)^2 = \frac{2}{3}a^2$,总表面积为$S_2 = 27 × \frac{2}{3}a^2 = 18a^2$,所以增加的表面积为$S_2 - S_1 = 12a^2$.
2. [2024·泉州二中月考]若正三棱台上、下底面边长分别是a和2a,棱台的高为$\frac{\sqrt{33}}{6}a$,则此正三棱台的侧面积为(
A.$a^{2}$
B.$\frac{1}{2}a^{2}$
C.$\frac{9}{2}a^{2}$
D.$\frac{3}{2}a^{2}$
C
)A.$a^{2}$
B.$\frac{1}{2}a^{2}$
C.$\frac{9}{2}a^{2}$
D.$\frac{3}{2}a^{2}$
答案:
2.C 【解析】如图,$O_1$,$O$分别为上、下底面的中心,$D_1$,$D$分别是$AC$,$A_1C_1$的中点,连接$O_1D_1$,$OD$,$DD_1$,$OO_1$,过$D_1$作$D_1E \perp OD$于点$E$.在直角梯形$ODD_1O_1$中,$OD = \frac{1}{3} × \frac{\sqrt{3}}{2} × 2a = \frac{\sqrt{3}}{3}a$,$O_1D_1 = \frac{1}{3} × \frac{\sqrt{3}}{2} × a = \frac{\sqrt{3}}{6}a$,所以$DE = OD - O_1D_1 = \frac{\sqrt{3}}{6}a$.在$Rt \triangle DED_1$中,$D_1E = \frac{\sqrt{33}}{6}a$,则$D_1D = \sqrt{(\frac{\sqrt{3}}{6}a)^2 + (\frac{\sqrt{33}}{6}a)^2} = \sqrt{\frac{3}{36}a^2 + \frac{33}{36}a^2} = a$.所以$S_{侧} = 3 × \frac{1}{2}(a + 2a)a = \frac{9}{2}a^2$.

2.C 【解析】如图,$O_1$,$O$分别为上、下底面的中心,$D_1$,$D$分别是$AC$,$A_1C_1$的中点,连接$O_1D_1$,$OD$,$DD_1$,$OO_1$,过$D_1$作$D_1E \perp OD$于点$E$.在直角梯形$ODD_1O_1$中,$OD = \frac{1}{3} × \frac{\sqrt{3}}{2} × 2a = \frac{\sqrt{3}}{3}a$,$O_1D_1 = \frac{1}{3} × \frac{\sqrt{3}}{2} × a = \frac{\sqrt{3}}{6}a$,所以$DE = OD - O_1D_1 = \frac{\sqrt{3}}{6}a$.在$Rt \triangle DED_1$中,$D_1E = \frac{\sqrt{33}}{6}a$,则$D_1D = \sqrt{(\frac{\sqrt{3}}{6}a)^2 + (\frac{\sqrt{33}}{6}a)^2} = \sqrt{\frac{3}{36}a^2 + \frac{33}{36}a^2} = a$.所以$S_{侧} = 3 × \frac{1}{2}(a + 2a)a = \frac{9}{2}a^2$.

3. [2024·长沙一中月考]如图所示,圆形纸片的圆心为O,半径为6 cm,该纸片上的等边三角形ABC的中心为O,D,E,F为圆O上的点,$\triangle DBC$,$\triangle ECA$,$\triangle FAB$分别是以BC,CA,AB为底边的等腰三角形,沿虚线剪开后,分别以BC,CA,AB为折痕折起$\triangle DBC$,$\triangle ECA$,$\triangle FAB$,使得D,E,F重合,得到三棱锥,则当$\triangle ABC$的边长变化时,三棱锥的表面积S的取值范围是(

A.$(0,36\pi)$
B.$(0,27\sqrt{3})$
C.$(0,45 - 9\sqrt{3})$
D.$(0,54\sqrt{3})$
D
)
A.$(0,36\pi)$
B.$(0,27\sqrt{3})$
C.$(0,45 - 9\sqrt{3})$
D.$(0,54\sqrt{3})$
答案:
3.D 【解析】设三棱锥底面边长为$a$,则$0 < a < 6\sqrt{3}$.如图所示,连接$OD$交$BC$于点$G$,则$OD = 6$,$OG = \frac{\sqrt{3}}{6}a$,$DG = 6 - \frac{\sqrt{3}}{6}a$,故三棱锥的底面积为$\frac{\sqrt{3}}{4}a^2$,侧面积为$3 × \frac{1}{2}a × (6 - \frac{\sqrt{3}}{6}a) = 9a - \frac{\sqrt{3}}{4}a^2$,所以表面积为$S = 9a$,故$0 < S < 54\sqrt{3}$.故选D.

3.D 【解析】设三棱锥底面边长为$a$,则$0 < a < 6\sqrt{3}$.如图所示,连接$OD$交$BC$于点$G$,则$OD = 6$,$OG = \frac{\sqrt{3}}{6}a$,$DG = 6 - \frac{\sqrt{3}}{6}a$,故三棱锥的底面积为$\frac{\sqrt{3}}{4}a^2$,侧面积为$3 × \frac{1}{2}a × (6 - \frac{\sqrt{3}}{6}a) = 9a - \frac{\sqrt{3}}{4}a^2$,所以表面积为$S = 9a$,故$0 < S < 54\sqrt{3}$.故选D.

4. [2024·成都七中月考]过长方体一个顶点的三条棱长的比是1:2:3,体对角线的长是$2\sqrt{14}$,则这个长方体的体积是(
A.6
B.12
C.24
D.48
D
)A.6
B.12
C.24
D.48
答案:
4.D 【解析】设过长方体一个顶点的三条棱长分别为$x$,$2x$,$3x$,由体对角线长为$2\sqrt{14}$,得$x^2 + (2x)^2 + (3x)^2 = (2\sqrt{14})^2$,解得$x = 2$.所以三条棱长分别为2,4,6.所以$V_{长方体} = 2 × 4 × 6 = 48$.
5. [2024·邯郸一中月考](多选)在四面体P - ABC中,$PA = PB = PC = BC = 1$,则该四面体的体积可能是(
A.$\frac{\sqrt{2}}{3}$
B.$\frac{\sqrt{2}}{12}$
C.$\frac{\sqrt{3}}{12}$
D.$\frac{\sqrt{3}}{3}$
BC
)A.$\frac{\sqrt{2}}{3}$
B.$\frac{\sqrt{2}}{12}$
C.$\frac{\sqrt{3}}{12}$
D.$\frac{\sqrt{3}}{3}$
答案:
5.BC 【解析】由题意得,$\triangle PBC$是边长为1的正三角形,所以$S_{\triangle PBC} = \frac{\sqrt{3}}{4}$,设三棱锥$A - PBC$的高为$h$,则$0 < h \leq 1$,故$V_{三棱锥P - ABC} = V_{三棱锥A - PBC} = \frac{1}{3}S_{\triangle PBC} · h = \frac{1}{3} × \frac{\sqrt{3}}{4} × h = \frac{\sqrt{3}}{12}h \in (0, \frac{\sqrt{3}}{12}]$.故选BC.
6. [2024·杭州学军中学期中]已知一个三棱锥的上、下底面分别是边长为20 cm和30 cm的正三角形,侧面是全等的等腰梯形,且侧面面积等于上、下底面面积之和,则棱台的体积为
$1900 cm^3$
.
答案:
6.$1900 cm^3$ 【解析】如图所示,在三棱台$ABC - A'B'C'$中,$O'$,$O$分别为上、下底面的中心,$D'$,$D$分别为$BC$,$B'C'$的中点,连接$OO'$,$A'D'$,$AD$,$DD'$,则$DD'$是等腰梯形$BCC'B'$的高,记为$h_0$,所以$S_{侧} = 3 × \frac{1}{2} × (20 + 30)h_0 = 75h_0$,上、下底面面积之和为$S_{上} + S_{下} = \frac{\sqrt{3}}{4} × (20^2 + 30^2) = 325\sqrt{3} (cm^2)$.由$S_{侧} = S_{上} + S_{下}$,得$75h_0 = 325\sqrt{3}$,解得$h_0 = \frac{13\sqrt{3}}{3} cm$.因为$O'D' = \frac{1}{3} × \frac{\sqrt{3}}{2} × 20 = \frac{10\sqrt{3}}{3} (cm)$,$OD = \frac{1}{3} × \frac{\sqrt{3}}{2} × 30 = 5\sqrt{3} (cm)$,记棱台的高为$h$,所以$h = O'O = \sqrt{h_0^2 - (OD - O'D')^2} = \sqrt{(\frac{13\sqrt{3}}{3})^2 - (5\sqrt{3} - \frac{10\sqrt{3}}{3})^2} = 4\sqrt{3} (cm)$.所以棱台的体积$V = \frac{h}{3}(S_{上} + S_{下} + \sqrt{S_{上}S_{下}}) = \frac{4\sqrt{3}}{3} × (325\sqrt{3} + \frac{\sqrt{3}}{4} × 20 × 30) = 1900 (cm^3)$.

6.$1900 cm^3$ 【解析】如图所示,在三棱台$ABC - A'B'C'$中,$O'$,$O$分别为上、下底面的中心,$D'$,$D$分别为$BC$,$B'C'$的中点,连接$OO'$,$A'D'$,$AD$,$DD'$,则$DD'$是等腰梯形$BCC'B'$的高,记为$h_0$,所以$S_{侧} = 3 × \frac{1}{2} × (20 + 30)h_0 = 75h_0$,上、下底面面积之和为$S_{上} + S_{下} = \frac{\sqrt{3}}{4} × (20^2 + 30^2) = 325\sqrt{3} (cm^2)$.由$S_{侧} = S_{上} + S_{下}$,得$75h_0 = 325\sqrt{3}$,解得$h_0 = \frac{13\sqrt{3}}{3} cm$.因为$O'D' = \frac{1}{3} × \frac{\sqrt{3}}{2} × 20 = \frac{10\sqrt{3}}{3} (cm)$,$OD = \frac{1}{3} × \frac{\sqrt{3}}{2} × 30 = 5\sqrt{3} (cm)$,记棱台的高为$h$,所以$h = O'O = \sqrt{h_0^2 - (OD - O'D')^2} = \sqrt{(\frac{13\sqrt{3}}{3})^2 - (5\sqrt{3} - \frac{10\sqrt{3}}{3})^2} = 4\sqrt{3} (cm)$.所以棱台的体积$V = \frac{h}{3}(S_{上} + S_{下} + \sqrt{S_{上}S_{下}}) = \frac{4\sqrt{3}}{3} × (325\sqrt{3} + \frac{\sqrt{3}}{4} × 20 × 30) = 1900 (cm^3)$.

7. [2024·重庆调研]水晶是一种石英结晶体矿物,因其硬度、色泽、光学性质、稀缺性等,常被人们制作成饰品.如图所示,现有棱长为2 cm的正方体水晶一块,将其裁去八个相同的四面体,打磨成饰品,则该饰品的表面积为(
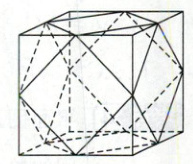
A.$(12 + 4\sqrt{3})cm^{2}$
B.$(16 + 4\sqrt{3})cm^{2}$
C.$(12 + 3\sqrt{3})cm^{2}$
D.$(16 + 3\sqrt{3})cm^{2}$
A
)
A.$(12 + 4\sqrt{3})cm^{2}$
B.$(16 + 4\sqrt{3})cm^{2}$
C.$(12 + 3\sqrt{3})cm^{2}$
D.$(16 + 3\sqrt{3})cm^{2}$
答案:
7.A 【解析】由题意得,该饰品的表面积为6个边长为$\sqrt{2} cm$的正方形与8个边长为$\sqrt{2} cm$的正三角形的面积之和,则该饰品的表面积$S = 6 × (\sqrt{2})^2 + 8 × \frac{\sqrt{3}}{4} × (\sqrt{2})^2 = (12 + 4\sqrt{3}) (cm^2)$.故选A.
8. [2024·吉安一中期末]司马迁在《史记·高祖本纪》中借刘邦之口赞美张良:“夫运筹策帷帐之中,决胜于千里之外.”帷帐又名帷幄,是古代行军打仗必备的帐篷.如图是一种帷帐的简易直观图,帐顶采用“五脊四坡式”,正脊平行于底面,四条斜脊长度均相等,帷帐主体部分可以看作一个长方体.若该帷帐主体部分长10,宽6,高4,帐顶部分正脊长4,斜脊长$\sqrt{34}$,则它的体积为

336
.
答案:
8.336 【解析】如图所示,过点$A$,$B$分别作$AN$,$BM$垂直于底面,垂足分别为$N$,$M$,过点$M$,$N$分别作宽的平行线$CF$,$DE$,连接$AC$,$AF$,$BD$,$BE$,则帐顶部分被分割成3部分,中间一部分是直三棱柱,两边是相同的四棱锥.由题意,得$CD = AB = 4$,$DM = \frac{1}{2}DE = 3$,则$BD = \sqrt{(\sqrt{34})^2 - 3^2} = 5$,$BM = \sqrt{BD^2 - DM^2} = \sqrt{5^2 - 3^2} = 4$,所以帐顶部分的体积$V_1 = 2 × \frac{1}{3} × 6 × 3 × 4 + \frac{1}{2} × 6 × 4 × 4 = 96$.又底部长方体的体积$V_2 = 10 × 6 × 4 = 240$,所以总体积$V = V_1 + V_2 = 336$.

8.336 【解析】如图所示,过点$A$,$B$分别作$AN$,$BM$垂直于底面,垂足分别为$N$,$M$,过点$M$,$N$分别作宽的平行线$CF$,$DE$,连接$AC$,$AF$,$BD$,$BE$,则帐顶部分被分割成3部分,中间一部分是直三棱柱,两边是相同的四棱锥.由题意,得$CD = AB = 4$,$DM = \frac{1}{2}DE = 3$,则$BD = \sqrt{(\sqrt{34})^2 - 3^2} = 5$,$BM = \sqrt{BD^2 - DM^2} = \sqrt{5^2 - 3^2} = 4$,所以帐顶部分的体积$V_1 = 2 × \frac{1}{3} × 6 × 3 × 4 + \frac{1}{2} × 6 × 4 × 4 = 96$.又底部长方体的体积$V_2 = 10 × 6 × 4 = 240$,所以总体积$V = V_1 + V_2 = 336$.

查看更多完整答案,请扫码查看


