2025年热搜题高中数学必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年热搜题高中数学必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. [2024·威海一中月考](多选)已知 $ a = (1,0),|b| = 1,c = (0,-1) $,满足 $ 3a + kb + 7c = 0 $,则实数 $ k $ 的值可能为(
A.$ \sqrt{58} $
B.$ -\sqrt{58} $
C.58
D.-58
AB
)A.$ \sqrt{58} $
B.$ -\sqrt{58} $
C.58
D.-58
答案:
1.AB [解析]由题可得,$kb = - 3a - 7c = - 3 × (1,0) - 7 × (0, - 1) = ( - 3,7)$,所以$|kb| = |k| · |b| = \sqrt{( - 3)^{2} + 7^{2}} = \sqrt{58}$.因为$|b| = 1$,所以$k = \pm \sqrt{58}$.故选AB.
2. [2024·南京外国语学校月考](多选)若向量 $ a = (\sqrt{3},3),b = (n,\sqrt{3}) $,下列结论正确的有(
A.若 $ a,b $ 同向,则 $ n = 1 $
B.与 $ a $ 垂直的单位向量一定是 $ (-\frac{\sqrt{3}}{2},\frac{1}{2}) $
C.若 $ b $ 在 $ a $ 上的投影向量为 $ 3e $($ e $ 是与向量 $ a $ 同向的单位向量),则 $ n = 3 $
D.若 $ a $ 与 $ b $ 的夹角为锐角,则 $ n $ 的取值范围是 $ (-3,+\infty) $
AC
)A.若 $ a,b $ 同向,则 $ n = 1 $
B.与 $ a $ 垂直的单位向量一定是 $ (-\frac{\sqrt{3}}{2},\frac{1}{2}) $
C.若 $ b $ 在 $ a $ 上的投影向量为 $ 3e $($ e $ 是与向量 $ a $ 同向的单位向量),则 $ n = 3 $
D.若 $ a $ 与 $ b $ 的夹角为锐角,则 $ n $ 的取值范围是 $ (-3,+\infty) $
答案:
2.AC [解析]设$a = kb(k > 0)$,所以$\begin{cases} kn = \sqrt{3}, \\ \sqrt{3}k = 3, \end{cases}$解得$\begin{cases} k = \sqrt{3}, \\n = 1, \end{cases}$即$a = \sqrt{3}b$,故A正确.
设$c = (x,y)$是与$a$垂直的单位向量,则有$\sqrt{3}x + 3y = 0$,$x^{2} + y^{2} = 1$,所以$c = ( - \frac{\sqrt{3}}{2},\frac{1}{2})$或$c = (\frac{\sqrt{3}}{2}, - \frac{1}{2})$,故B错误.
因为$b$在$a$上的投影向量为$3e$,所以$\frac{a · b}{|a|} = 3$,所以$\frac{\sqrt{3}n + 3\sqrt{3}}{2\sqrt{3}} = 3$,解得$n = 3$,故C正确.
因为$a$与$b$的夹角为锐角,所以$a · b > 0$且$a,b$不共线,所以$\begin{cases} \sqrt{3}n + 3\sqrt{3} > 0, \\3 - 3n \neq 0, \end{cases}$解得$\begin{cases} n > - 3, \\n \neq 1, \end{cases}$所以$n \in ( - 3,1) \cup (1, + \infty)$,故D错误.故选AC.
设$c = (x,y)$是与$a$垂直的单位向量,则有$\sqrt{3}x + 3y = 0$,$x^{2} + y^{2} = 1$,所以$c = ( - \frac{\sqrt{3}}{2},\frac{1}{2})$或$c = (\frac{\sqrt{3}}{2}, - \frac{1}{2})$,故B错误.
因为$b$在$a$上的投影向量为$3e$,所以$\frac{a · b}{|a|} = 3$,所以$\frac{\sqrt{3}n + 3\sqrt{3}}{2\sqrt{3}} = 3$,解得$n = 3$,故C正确.
因为$a$与$b$的夹角为锐角,所以$a · b > 0$且$a,b$不共线,所以$\begin{cases} \sqrt{3}n + 3\sqrt{3} > 0, \\3 - 3n \neq 0, \end{cases}$解得$\begin{cases} n > - 3, \\n \neq 1, \end{cases}$所以$n \in ( - 3,1) \cup (1, + \infty)$,故D错误.故选AC.
3. [2024·长沙长郡中学月考]已知向量 $ a $ 与 $ b $ 的夹角为 $ \theta $,定义 $ a × b $ 为 $ a $ 与 $ b $ 的“向量积”,且 $ a × b $ 是一个向量,它的长度 $ |a × b| = |a| · |b| \sin \theta $,若 $ u = (2,0),u - v = (1,-\sqrt{3}) $,则 $ |u × (u + v)| = $(
A.$ 4\sqrt{3} $
B.$ \sqrt{3} $
C.6
D.$ 2\sqrt{3} $
D
)A.$ 4\sqrt{3} $
B.$ \sqrt{3} $
C.6
D.$ 2\sqrt{3} $
答案:
3.D [解析]由题意得$v = u - (u - v) = (1,\sqrt{3})$,则$u + v = (3,\sqrt{3})$,所以$u · (u + v) = 6$,$|u + v| = \sqrt{3^{2} + (\sqrt{3})^{2}} = 2\sqrt{3}$.因为$|u| = 2$,所以$\cos\langle u,u + v\rangle = \frac{u · (u + v)}{|u||u + v|} = \frac{6}{2 × 2\sqrt{3}} = \frac{\sqrt{3}}{2}$.所以$\sin\langle u,u + v\rangle = \frac{1}{2}$,由定义知$|u × (u + v)| = |u||u + v| · \sin\langle u,u + v\rangle = 2 × 2\sqrt{3} × \frac{1}{2} = 2\sqrt{3}$.
4. [2024·福州一中期末]骑自行车是一种既环保又健康的运动,如图是某自行车的平面结构示意图.已知图中的圆 $ A $(前轮)、圆 $ D $(后轮)的半径均为 $ \sqrt{3} $,$ \triangle ABE,\triangle BEC,\triangle ECD $ 均是边长为 4 的等边三角形.设 $ P $ 为后轮上的一点,则在骑自行车的过程中,$ \overrightarrow{AC} · \overrightarrow{AP} $ 的最大值为(
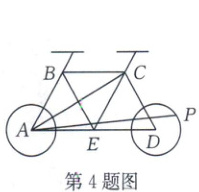
A.48
B.36
C.72
D.60
D
)
A.48
B.36
C.72
D.60
答案:
4.D [解析]以A为坐标原点,AD所在直线为x轴建立平面直角坐标系,如图所示.

因为$\triangle ABE,\triangle BEC,\triangle ECD$均是边长为$4$的等边三角形,所以$A(0,0),C(6,2\sqrt{3})$,所以$\overrightarrow{AC} = (6,2\sqrt{3})$.连接PD,设$\angle PDA = \theta$,则点$P(8 + \sqrt{3}\cos\theta,\sqrt{3}\sin\theta)$,所以$\overrightarrow{AC} · \overrightarrow{AP} = 48 + 6\sqrt{3}\cos\theta + 6\sin\theta = 12\sin(\theta + \frac{\pi}{3}) + 48 \in [36,60]$.故选D.
4.D [解析]以A为坐标原点,AD所在直线为x轴建立平面直角坐标系,如图所示.

因为$\triangle ABE,\triangle BEC,\triangle ECD$均是边长为$4$的等边三角形,所以$A(0,0),C(6,2\sqrt{3})$,所以$\overrightarrow{AC} = (6,2\sqrt{3})$.连接PD,设$\angle PDA = \theta$,则点$P(8 + \sqrt{3}\cos\theta,\sqrt{3}\sin\theta)$,所以$\overrightarrow{AC} · \overrightarrow{AP} = 48 + 6\sqrt{3}\cos\theta + 6\sin\theta = 12\sin(\theta + \frac{\pi}{3}) + 48 \in [36,60]$.故选D.
5. [2024·西安一中期末]如图,在 $ \triangle ABC $ 中, $ D,E,F $ 分别为 $ BC,CA,AB $ 上的点,且 $ CD = \frac{3}{5}BC,EC = \frac{1}{2}AC,AF = \frac{1}{3}AB $.设 $ P $ 为四边形 $ AEDF $ 内一点($ P $ 点不在边界上).若 $ \overrightarrow{DP} = -\frac{1}{3}\overrightarrow{DC} + \lambda \overrightarrow{DE} $,则实数 $ \lambda $ 的取值范围为
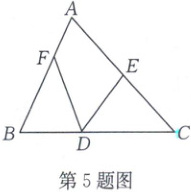
$(\frac{1}{2},\frac{4}{3})$
.
答案:
5.$(\frac{1}{2},\frac{4}{3})$ [解析]取BD中点M,过M作MH // DE分别交DF,AC于点G,H,连接FH,延长FH,交DE的延长线于点K,可得FK // BC,过G作GN // BC,交DE于点N,如图,则由$\overrightarrow{DP} = - \frac{1}{3}\overrightarrow{DC} + \lambda\overrightarrow{DE} = \overrightarrow{DM} + \lambda\overrightarrow{DE}$可知,$P$在线段GH上运动(不包括端点).当P与G重合时,根据$\overrightarrow{DP} = t\overrightarrow{DF} = t(\overrightarrow{BF} - \overrightarrow{BD}) = t(\frac{2}{3}\overrightarrow{BA} - \frac{2}{3}\overrightarrow{DC}) = \frac{2}{3}t(\overrightarrow{BD} + \overrightarrow{DA}) - \frac{2}{3}t\overrightarrow{DC} = - \frac{8}{9}t\overrightarrow{DC} + \frac{4}{3}t\overrightarrow{DE} = - \frac{1}{3}\overrightarrow{DC} + \lambda\overrightarrow{DE}$,可知$\lambda = \frac{1}{2}$,当P与H重合时,由P,C,E共线可知$- \frac{1}{3} + \lambda = 1$,即$\lambda = \frac{4}{3}$,结合图形可知$\lambda \in (\frac{1}{2},\frac{4}{3})$.

5.$(\frac{1}{2},\frac{4}{3})$ [解析]取BD中点M,过M作MH // DE分别交DF,AC于点G,H,连接FH,延长FH,交DE的延长线于点K,可得FK // BC,过G作GN // BC,交DE于点N,如图,则由$\overrightarrow{DP} = - \frac{1}{3}\overrightarrow{DC} + \lambda\overrightarrow{DE} = \overrightarrow{DM} + \lambda\overrightarrow{DE}$可知,$P$在线段GH上运动(不包括端点).当P与G重合时,根据$\overrightarrow{DP} = t\overrightarrow{DF} = t(\overrightarrow{BF} - \overrightarrow{BD}) = t(\frac{2}{3}\overrightarrow{BA} - \frac{2}{3}\overrightarrow{DC}) = \frac{2}{3}t(\overrightarrow{BD} + \overrightarrow{DA}) - \frac{2}{3}t\overrightarrow{DC} = - \frac{8}{9}t\overrightarrow{DC} + \frac{4}{3}t\overrightarrow{DE} = - \frac{1}{3}\overrightarrow{DC} + \lambda\overrightarrow{DE}$,可知$\lambda = \frac{1}{2}$,当P与H重合时,由P,C,E共线可知$- \frac{1}{3} + \lambda = 1$,即$\lambda = \frac{4}{3}$,结合图形可知$\lambda \in (\frac{1}{2},\frac{4}{3})$.

6. [天津卷]在边长为 1 的等边三角形 $ ABC $ 中,$ D $ 为线段 $ BC $ 上的动点,$ DE \perp AB $ 且交 $ AB $ 于点 $ E,DF // AB $ 且交 $ AC $ 于点 $ F $,则 $ |2\overrightarrow{BE} + \overrightarrow{DF}| $ 的值为
1
;$ (\overrightarrow{DE} + \overrightarrow{DF}) · \overrightarrow{DA} $ 的最小值为$\frac{11}{20}$
.
答案:
6.$1,\frac{11}{20}$ [解析]如图,过点F作FG⊥AB,交AB于点G,易证得$\triangle BED \cong \triangle AGF$,四边形EDFG是矩形,所以$BE = GA$,$DF = EG$,则$2BE + DF = BE + GA + EG = BA$,所以$|2BE + DF| = |BA| = 1$.连接DG,则$\overrightarrow{DE} + \overrightarrow{DF} = \overrightarrow{DG}$,则$(\overrightarrow{DE} + \overrightarrow{DF}) · \overrightarrow{DA} = \overrightarrow{DG} · \overrightarrow{DA}$.以B为坐标原点,BC所在直线为x轴建立平面直角坐标系,设$|BD| = 2t(0 < t < \frac{1}{2})$,则$|BG| = 1 - t$,$D(2t,0)$,$A(\frac{1}{2},\frac{\sqrt{3}}{2})$,$G(\frac{1 - t}{2},\frac{\sqrt{3}(1 - t)}{2})$,所以$\overrightarrow{DG} = (\frac{1 - 5t}{2},\frac{\sqrt{3}(1 - t)}{2})$,$\overrightarrow{DA} = (\frac{1}{2} - 2t,\frac{\sqrt{3}}{2})$,所以$\overrightarrow{DG} · \overrightarrow{DA} = 5t^{2} - 3t + 1 = 5(t - \frac{3}{10})^{2} + \frac{11}{20}$,所以当$t = \frac{3}{10}$时,$\overrightarrow{DG} · \overrightarrow{DA}$取得最小值,最小值为$\frac{11}{20}$,即$(\overrightarrow{DE} + \overrightarrow{DF}) · \overrightarrow{DA}$的最小值为$\frac{11}{20}$.

6.$1,\frac{11}{20}$ [解析]如图,过点F作FG⊥AB,交AB于点G,易证得$\triangle BED \cong \triangle AGF$,四边形EDFG是矩形,所以$BE = GA$,$DF = EG$,则$2BE + DF = BE + GA + EG = BA$,所以$|2BE + DF| = |BA| = 1$.连接DG,则$\overrightarrow{DE} + \overrightarrow{DF} = \overrightarrow{DG}$,则$(\overrightarrow{DE} + \overrightarrow{DF}) · \overrightarrow{DA} = \overrightarrow{DG} · \overrightarrow{DA}$.以B为坐标原点,BC所在直线为x轴建立平面直角坐标系,设$|BD| = 2t(0 < t < \frac{1}{2})$,则$|BG| = 1 - t$,$D(2t,0)$,$A(\frac{1}{2},\frac{\sqrt{3}}{2})$,$G(\frac{1 - t}{2},\frac{\sqrt{3}(1 - t)}{2})$,所以$\overrightarrow{DG} = (\frac{1 - 5t}{2},\frac{\sqrt{3}(1 - t)}{2})$,$\overrightarrow{DA} = (\frac{1}{2} - 2t,\frac{\sqrt{3}}{2})$,所以$\overrightarrow{DG} · \overrightarrow{DA} = 5t^{2} - 3t + 1 = 5(t - \frac{3}{10})^{2} + \frac{11}{20}$,所以当$t = \frac{3}{10}$时,$\overrightarrow{DG} · \overrightarrow{DA}$取得最小值,最小值为$\frac{11}{20}$,即$(\overrightarrow{DE} + \overrightarrow{DF}) · \overrightarrow{DA}$的最小值为$\frac{11}{20}$.

7. [2024·黄冈中学月考]已知点 $ A(2,0) $,$ B(0,2),C(\cos \alpha,\sin \alpha) $(其中 $ 0 < \alpha < \pi $),$ O $ 为坐标原点.
(1)若 $ |\overrightarrow{OA} + \overrightarrow{OC}| = \sqrt{7} $,则 $ \overrightarrow{OB} $ 与 $ \overrightarrow{OC} $ 的夹角为
(2)若 $ \overrightarrow{AC} \perp \overrightarrow{BC} $,则 $ \tan \alpha $ 的值为
(1)若 $ |\overrightarrow{OA} + \overrightarrow{OC}| = \sqrt{7} $,则 $ \overrightarrow{OB} $ 与 $ \overrightarrow{OC} $ 的夹角为
$\frac{\pi}{6}$
;(2)若 $ \overrightarrow{AC} \perp \overrightarrow{BC} $,则 $ \tan \alpha $ 的值为
$-\frac{4+\sqrt{7}}{3}$
.
答案:
7.
(1)$\frac{\pi}{6}$
(2)$- \frac{4 + \sqrt{7}}{3}$ [解析]
(1)由已知得$\overrightarrow{OA} + \overrightarrow{OC} = (2 + \cos\alpha,\sin\alpha)$.因为$|\overrightarrow{OA} + \overrightarrow{OC}| = \sqrt{7}$,所以$(2 + \cos\alpha)^{2} + \sin^{2}\alpha = 7$,即$4 + 4\cos\alpha + \cos^{2}\alpha + \sin^{2}\alpha = 7$.所以$\cos\alpha = \frac{1}{2}$.又$\alpha \in (0,\pi)$,所以$\alpha = \frac{\pi}{3}$,所以$\sin\alpha = \frac{\sqrt{3}}{2}$,所以$\overrightarrow{OC} = (\frac{1}{2},\frac{\sqrt{3}}{2})$.
又因为$\overrightarrow{OB} = (0,2)$,所以$\cos\angle BOC = \frac{\overrightarrow{OB} · \overrightarrow{OC}}{|\overrightarrow{OB}||\overrightarrow{OC}|} = \frac{\sqrt{3}}{2}$.又$0 \leq \angle BOC \leq \pi$,所以$\angle BOC = \frac{\pi}{6}$.故$\overrightarrow{OB}$与$\overrightarrow{OC}$的夹角为$\frac{\pi}{6}$.
(2)由已知得$\overrightarrow{AC} = (\cos\alpha - 2,\sin\alpha),\overrightarrow{BC} = (\cos\alpha,\sin\alpha - 2)$.因为$\overrightarrow{AC} \perp \overrightarrow{BC}$,所以$\overrightarrow{AC} · \overrightarrow{BC} = 0$,故$\cos\alpha(\cos\alpha - 2) + \sin\alpha(\sin\alpha - 2) = 0$,即$\sin\alpha + \cos\alpha = \frac{1}{2}$,两边平方得$(\sin\alpha + \cos\alpha)^{2} = \frac{1}{4}$即$2\sin\alpha\cos\alpha + \frac{3}{4} = 0$,即$2\sin\alpha\cos\alpha + \frac{3}{4}(\sin^{2}\alpha + \cos^{2}\alpha) = 0$,所以$3\sin^{2}\alpha + 8\sin\alpha\cos\alpha + 3\cos^{2}\alpha = 0$.由①可知,$\cos\alpha \neq 0$,两边同时除以$\cos^{2}\alpha$,得$3\tan^{2}\alpha + 8\tan\alpha + 3 = 0$,所以$\tan\alpha = \frac{- 8 \pm \sqrt{28}}{6} = \frac{- 4 \pm \sqrt{7}}{3}$.因为$2\sin\alpha\cos\alpha = - \frac{3}{4} < 0,\alpha \in (0,\pi)$,所以$\sin\alpha > 0,\cos\alpha < 0$.又因为$\sin\alpha + \cos\alpha = \frac{1}{2} > 0$,所以$\sin\alpha > - \cos\alpha$,所以$\frac{\sin\alpha}{\cos\alpha} < - 1$,即$\tan\alpha < - 1$,而$\tan\alpha = \frac{- 4 + \sqrt{7}}{3} > - 1$,舍去.故$\tan\alpha = - \frac{4 + \sqrt{7}}{3}$.
(1)$\frac{\pi}{6}$
(2)$- \frac{4 + \sqrt{7}}{3}$ [解析]
(1)由已知得$\overrightarrow{OA} + \overrightarrow{OC} = (2 + \cos\alpha,\sin\alpha)$.因为$|\overrightarrow{OA} + \overrightarrow{OC}| = \sqrt{7}$,所以$(2 + \cos\alpha)^{2} + \sin^{2}\alpha = 7$,即$4 + 4\cos\alpha + \cos^{2}\alpha + \sin^{2}\alpha = 7$.所以$\cos\alpha = \frac{1}{2}$.又$\alpha \in (0,\pi)$,所以$\alpha = \frac{\pi}{3}$,所以$\sin\alpha = \frac{\sqrt{3}}{2}$,所以$\overrightarrow{OC} = (\frac{1}{2},\frac{\sqrt{3}}{2})$.
又因为$\overrightarrow{OB} = (0,2)$,所以$\cos\angle BOC = \frac{\overrightarrow{OB} · \overrightarrow{OC}}{|\overrightarrow{OB}||\overrightarrow{OC}|} = \frac{\sqrt{3}}{2}$.又$0 \leq \angle BOC \leq \pi$,所以$\angle BOC = \frac{\pi}{6}$.故$\overrightarrow{OB}$与$\overrightarrow{OC}$的夹角为$\frac{\pi}{6}$.
(2)由已知得$\overrightarrow{AC} = (\cos\alpha - 2,\sin\alpha),\overrightarrow{BC} = (\cos\alpha,\sin\alpha - 2)$.因为$\overrightarrow{AC} \perp \overrightarrow{BC}$,所以$\overrightarrow{AC} · \overrightarrow{BC} = 0$,故$\cos\alpha(\cos\alpha - 2) + \sin\alpha(\sin\alpha - 2) = 0$,即$\sin\alpha + \cos\alpha = \frac{1}{2}$,两边平方得$(\sin\alpha + \cos\alpha)^{2} = \frac{1}{4}$即$2\sin\alpha\cos\alpha + \frac{3}{4} = 0$,即$2\sin\alpha\cos\alpha + \frac{3}{4}(\sin^{2}\alpha + \cos^{2}\alpha) = 0$,所以$3\sin^{2}\alpha + 8\sin\alpha\cos\alpha + 3\cos^{2}\alpha = 0$.由①可知,$\cos\alpha \neq 0$,两边同时除以$\cos^{2}\alpha$,得$3\tan^{2}\alpha + 8\tan\alpha + 3 = 0$,所以$\tan\alpha = \frac{- 8 \pm \sqrt{28}}{6} = \frac{- 4 \pm \sqrt{7}}{3}$.因为$2\sin\alpha\cos\alpha = - \frac{3}{4} < 0,\alpha \in (0,\pi)$,所以$\sin\alpha > 0,\cos\alpha < 0$.又因为$\sin\alpha + \cos\alpha = \frac{1}{2} > 0$,所以$\sin\alpha > - \cos\alpha$,所以$\frac{\sin\alpha}{\cos\alpha} < - 1$,即$\tan\alpha < - 1$,而$\tan\alpha = \frac{- 4 + \sqrt{7}}{3} > - 1$,舍去.故$\tan\alpha = - \frac{4 + \sqrt{7}}{3}$.
8. [2024·六安一中期中]在①$ (ta + b) \perp (a + tb) $,②$ |ta + b| = |a + tb| $,③$ \langle ta + b,b \rangle = 45^{\circ} $这三个条件中任选一个,补充在下面问题中,并解答问题.
已知向量 $ a = (-1,-1),b = (0,1) $.
(1)若,求实数 $ t $ 的值;
(2)若向量 $ c = (x,y) $,且 $ c = -ya + (1 - x)b $,求 $ |c| $.
注:若选择多个条件分别解答,则按第一个解答计分.
已知向量 $ a = (-1,-1),b = (0,1) $.
(1)若,求实数 $ t $ 的值;
(2)若向量 $ c = (x,y) $,且 $ c = -ya + (1 - x)b $,求 $ |c| $.
注:若选择多个条件分别解答,则按第一个解答计分.
答案:
8.
(1)若选择条件①.由题意,得$t\overrightarrow{a} + \overrightarrow{b} = ( - t,1 - t),\overrightarrow{a} + t\overrightarrow{b} = ( - 1,t - 1)$,因为$(t\overrightarrow{a} + \overrightarrow{b}) \perp (\overrightarrow{a} + t\overrightarrow{b})$,所以$(t\overrightarrow{a} + \overrightarrow{b}) · (\overrightarrow{a} + t\overrightarrow{b}) = 0$,所以$t + (1 - t)(t - 1) = 0$,即$t^{2} - 3t + 1 = 0$,解得$t = \frac{3 \pm \sqrt{5}}{2}$.
若选择条件②.由题意,得$t\overrightarrow{a} + \overrightarrow{b} = ( - t,1 - t),\overrightarrow{a} + t\overrightarrow{b} = ( - 1,t - 1)$,因为$|t\overrightarrow{a} + \overrightarrow{b}| = |\overrightarrow{a} + t\overrightarrow{b}|$,所以$\sqrt{( - t)^{2} + (1 - t)^{2}} = \sqrt{( - 1)^{2} + (t - 1)^{2}}$,即$t^{2} = 1$,解得$t = \pm 1$.
若选择条件③.由题意,得$t\overrightarrow{a} + \overrightarrow{b} = ( - t,1 - t)$,所以$\cos\langle t\overrightarrow{a} + \overrightarrow{b},\overrightarrow{b}\rangle = \frac{(t\overrightarrow{a} + \overrightarrow{b}) · \overrightarrow{b}}{|t\overrightarrow{a} + \overrightarrow{b}||\overrightarrow{b}|} = \frac{1 - t}{\sqrt{t^{2} + (1 - t)^{2}}} = \frac{\sqrt{2}}{2}$,解得$t = \frac{1}{2}$.
(2)因为$\overrightarrow{c} = - y\overrightarrow{a} + (1 - x)\overrightarrow{b}$,所以$(x,y) = (y,1 - x + y)$,即$\begin{cases} x = y, \\y = 1 - x + y,\end{cases}$解得$\begin{cases} x = 1, \\y = 1,\end{cases}$所以$\overrightarrow{c} = (1,1)$,所以$|\overrightarrow{c}| = \sqrt{1^{2} + 1^{2}} = \sqrt{2}$.
(1)若选择条件①.由题意,得$t\overrightarrow{a} + \overrightarrow{b} = ( - t,1 - t),\overrightarrow{a} + t\overrightarrow{b} = ( - 1,t - 1)$,因为$(t\overrightarrow{a} + \overrightarrow{b}) \perp (\overrightarrow{a} + t\overrightarrow{b})$,所以$(t\overrightarrow{a} + \overrightarrow{b}) · (\overrightarrow{a} + t\overrightarrow{b}) = 0$,所以$t + (1 - t)(t - 1) = 0$,即$t^{2} - 3t + 1 = 0$,解得$t = \frac{3 \pm \sqrt{5}}{2}$.
若选择条件②.由题意,得$t\overrightarrow{a} + \overrightarrow{b} = ( - t,1 - t),\overrightarrow{a} + t\overrightarrow{b} = ( - 1,t - 1)$,因为$|t\overrightarrow{a} + \overrightarrow{b}| = |\overrightarrow{a} + t\overrightarrow{b}|$,所以$\sqrt{( - t)^{2} + (1 - t)^{2}} = \sqrt{( - 1)^{2} + (t - 1)^{2}}$,即$t^{2} = 1$,解得$t = \pm 1$.
若选择条件③.由题意,得$t\overrightarrow{a} + \overrightarrow{b} = ( - t,1 - t)$,所以$\cos\langle t\overrightarrow{a} + \overrightarrow{b},\overrightarrow{b}\rangle = \frac{(t\overrightarrow{a} + \overrightarrow{b}) · \overrightarrow{b}}{|t\overrightarrow{a} + \overrightarrow{b}||\overrightarrow{b}|} = \frac{1 - t}{\sqrt{t^{2} + (1 - t)^{2}}} = \frac{\sqrt{2}}{2}$,解得$t = \frac{1}{2}$.
(2)因为$\overrightarrow{c} = - y\overrightarrow{a} + (1 - x)\overrightarrow{b}$,所以$(x,y) = (y,1 - x + y)$,即$\begin{cases} x = y, \\y = 1 - x + y,\end{cases}$解得$\begin{cases} x = 1, \\y = 1,\end{cases}$所以$\overrightarrow{c} = (1,1)$,所以$|\overrightarrow{c}| = \sqrt{1^{2} + 1^{2}} = \sqrt{2}$.
查看更多完整答案,请扫码查看


