2025年热搜题高中数学必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年热搜题高中数学必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
4. [2024·烟台一中月考]已知$E$为平面内一定点且$|\overrightarrow{OE}|=1$,平面内的动点$P$满足:$\exists\lambda\geq1$,使$|\lambda\overrightarrow{OP}+(1-\lambda)\overrightarrow{OE}|=\frac{1}{2}$,求点$P$的轨迹所形成的平面图形的面积。
答案:
4.以 $O$ 为圆心,$\frac{1}{2}$ 为半径作圆,过 $E$ 作圆 $O$ 的切线 $EA$,$EB$ 分别与圆 $O$ 相切于点 $A$,$B$,连接 $OA$,$OB$,延长 $EO$ 与圆 $O$ 交于点 $F$,如图所示. 设点 $Q$ 满足 $\overrightarrow{OQ}=\lambda\overrightarrow{OP}+(1-\lambda)\overrightarrow{OE}$,则 $\overrightarrow{OQ}-\overrightarrow{OE}=\lambda\overrightarrow{OP}-\lambda\overrightarrow{OE}$,即 $\overrightarrow{EQ}=\lambda\overrightarrow{EP}$,由 $\lambda\geqslant1$,可知点 $Q$ 在 $EP$ 的延长线上. 若要存在 $\lambda\geqslant1$ 使得 $|\overrightarrow{OQ}|=\frac{1}{2}$,相当于 $EP$ 的延长线与圆 $O$ 有交点,故点 $P$ 只能在图中阴影部分,所以点 $P$ 的轨迹所形成的平面图形的面积 $S=S_{\triangle AOE}+S_{\triangle BOE}+S_{扇形AOF}+S_{扇形BOF}$. 因为 $EA$ 与圆 $O$ 相切于点 $A$,所以 $OA\perp AE$,且 $OA=\frac{1}{2}$,$OE=1$,由勾股定理可知,$AE=\frac{\sqrt{3}}{2}$,所以 $S_{\triangle AOE}=\frac{\sqrt{3}}{8}$,同理可得 $S_{\triangle BOE}=\frac{\sqrt{3}}{8}$. 易知 $\angle AOE=60^{\circ}$,所以 $\angle AOF=120^{\circ}$,所以 $S_{扇形AOF}=\frac{1}{3}×\pi×(\frac{1}{2})^2=\frac{\pi}{12}$,同理可得 $S_{扇形BOF}=\frac{\pi}{12}$,所以 $S=\frac{\sqrt{3}}{8}+\frac{\sqrt{3}}{8}+\frac{\pi}{12}+\frac{\pi}{12}=\frac{\sqrt{3}}{4}+\frac{\pi}{6}$. 综上所述,点 $P$ 的轨迹所形成的平面图形的面积为 $\frac{\sqrt{3}}{4}+\frac{\pi}{6}$.
4.以 $O$ 为圆心,$\frac{1}{2}$ 为半径作圆,过 $E$ 作圆 $O$ 的切线 $EA$,$EB$ 分别与圆 $O$ 相切于点 $A$,$B$,连接 $OA$,$OB$,延长 $EO$ 与圆 $O$ 交于点 $F$,如图所示. 设点 $Q$ 满足 $\overrightarrow{OQ}=\lambda\overrightarrow{OP}+(1-\lambda)\overrightarrow{OE}$,则 $\overrightarrow{OQ}-\overrightarrow{OE}=\lambda\overrightarrow{OP}-\lambda\overrightarrow{OE}$,即 $\overrightarrow{EQ}=\lambda\overrightarrow{EP}$,由 $\lambda\geqslant1$,可知点 $Q$ 在 $EP$ 的延长线上. 若要存在 $\lambda\geqslant1$ 使得 $|\overrightarrow{OQ}|=\frac{1}{2}$,相当于 $EP$ 的延长线与圆 $O$ 有交点,故点 $P$ 只能在图中阴影部分,所以点 $P$ 的轨迹所形成的平面图形的面积 $S=S_{\triangle AOE}+S_{\triangle BOE}+S_{扇形AOF}+S_{扇形BOF}$. 因为 $EA$ 与圆 $O$ 相切于点 $A$,所以 $OA\perp AE$,且 $OA=\frac{1}{2}$,$OE=1$,由勾股定理可知,$AE=\frac{\sqrt{3}}{2}$,所以 $S_{\triangle AOE}=\frac{\sqrt{3}}{8}$,同理可得 $S_{\triangle BOE}=\frac{\sqrt{3}}{8}$. 易知 $\angle AOE=60^{\circ}$,所以 $\angle AOF=120^{\circ}$,所以 $S_{扇形AOF}=\frac{1}{3}×\pi×(\frac{1}{2})^2=\frac{\pi}{12}$,同理可得 $S_{扇形BOF}=\frac{\pi}{12}$,所以 $S=\frac{\sqrt{3}}{8}+\frac{\sqrt{3}}{8}+\frac{\pi}{12}+\frac{\pi}{12}=\frac{\sqrt{3}}{4}+\frac{\pi}{6}$. 综上所述,点 $P$ 的轨迹所形成的平面图形的面积为 $\frac{\sqrt{3}}{4}+\frac{\pi}{6}$.

5. [2024·黄冈检测]在$\triangle ABC$所在平面内有一点$P$,满足$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{AB}$,则$\triangle PBC$与$\triangle ABC$的面积的比值是(
A.$\frac{1}{3}$
B.$\frac{1}{2}$
C.$\frac{2}{3}$
D.$\frac{3}{4}$
C
)A.$\frac{1}{3}$
B.$\frac{1}{2}$
C.$\frac{2}{3}$
D.$\frac{3}{4}$
答案:
5.C[解析]由 $\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{AB}$,得 $\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{BA}+\overrightarrow{PC}=0$,即 $\overrightarrow{PC}=2\overrightarrow{AP}$,所以 $P$ 是 $CA$ 边上的一个三等分点,且 $PC=2AP$,故 $\frac{S_{\triangle PBC}}{S_{\triangle ABC}}=\frac{2}{3}$.
6. [2024·泉州德化一中期末]已知$O$是$\triangle ABC$所在平面内一点,$D$为$BC$边的中点,且$2\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\boldsymbol{0}$,那么$\triangle ABC$的面积是$\triangle OBD$的面积的(
A.$2$倍
B.$3$倍
C.$4$倍
D.$6$倍
C
)A.$2$倍
B.$3$倍
C.$4$倍
D.$6$倍
答案:
6.C[解析]由题意得 $2\overrightarrow{OA}+2\overrightarrow{OD}=0$,所以 $\overrightarrow{OA}=\overrightarrow{DO}$,即 $O$ 为 $AD$ 中点,所以 $S_{\triangle ABC}=2S_{\triangle ABD}=4S_{\triangle OBD}$.
7. [2024·哈师大附中月考]在$\triangle ABC$中,$D$为$BC$的中点,$O$为$AD$的中点,过$O$作一直线分别交$AB,AC$于$M,N$两点,若$\overrightarrow{AM}=x\overrightarrow{AB}$,$\overrightarrow{AN}=y\overrightarrow{AC}(xy\neq0)$,则$\frac{1}{x}+\frac{1}{y}=$(
A.$3$
B.$2$
C.$4$
D.$\frac{1}{4}$
C
)A.$3$
B.$2$
C.$4$
D.$\frac{1}{4}$
答案:
7.C[解析]在 $\triangle ABC$ 中,$D$ 为 $BC$ 的中点,$O$ 为 $AD$ 的中点,若 $\overrightarrow{AM}=x\overrightarrow{AB}$,$\overrightarrow{AN}=y\overrightarrow{AC}$,则 $\overrightarrow{MO}=\overrightarrow{AO}-\overrightarrow{AM}=\frac{1}{2}\overrightarrow{AD}-\overrightarrow{AM}=\frac{1}{4}(\overrightarrow{AB}+\overrightarrow{AC})-x\overrightarrow{AB}=(\frac{1}{4}-x)\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$,$\overrightarrow{ON}=\overrightarrow{AN}-\overrightarrow{AO}=y\overrightarrow{AC}-\frac{1}{4}(\overrightarrow{AB}+\overrightarrow{AC})=-\frac{1}{4}\overrightarrow{AB}+(y-\frac{1}{4})\overrightarrow{AC}$. 因为 $\overrightarrow{MO}//\overrightarrow{ON}$,所以设 $\overrightarrow{MO}=\lambda\overrightarrow{ON}$,则 $(\frac{1}{4}-x+\frac{1}{4}\lambda)\overrightarrow{AB}=[\lambda(y-\frac{1}{4})-\frac{1}{4}]\overrightarrow{AC}$. 因为 $\overrightarrow{AB}$,$\overrightarrow{AC}$ 不共线,所以 $\begin{cases}\frac{1}{4}-x+\frac{1}{4}\lambda=0,\\\lambda(y-\frac{1}{4})-\frac{1}{4}=0,\end{cases}$ 所以 $\frac{1}{4}(x+y)-xy=0$,整理得 $\frac{1}{x}+\frac{1}{y}=4$. 故选C.
8. 在$\triangle ABC$中,若点$P$满足$\overrightarrow{AP}=\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$,点$Q$满足$\overrightarrow{AQ}=\frac{3}{4}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$,则$\triangle APQ$与$\triangle ABC$的面积的比值为(
A.$\frac{1}{3}$
B.$\frac{5}{12}$
C.$\frac{3}{4}$
D.$\frac{9}{16}$
B
)A.$\frac{1}{3}$
B.$\frac{5}{12}$
C.$\frac{3}{4}$
D.$\frac{9}{16}$
答案:
8.B[解析]因为 $\overrightarrow{AP}=\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$,所以 $\frac{1}{3}(\overrightarrow{AP}-\overrightarrow{AB})=\frac{2}{3}(\overrightarrow{AC}-\overrightarrow{AP})$,即 $\overrightarrow{BP}=2\overrightarrow{PC}$,所以 $P$ 为线段 $BC$ 上靠近 $C$ 点的三等分点. 又 $\overrightarrow{AQ}=\frac{3}{4}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$,所以 $\frac{3}{4}(\overrightarrow{AQ}-\overrightarrow{AB})=\frac{1}{4}(\overrightarrow{AC}-\overrightarrow{AQ})$,即 $3\overrightarrow{BQ}=\overrightarrow{QC}$,所以 $Q$ 为线段 $BC$ 上靠近 $B$ 点的四等分点,所以 $PQ=\frac{5}{12}BC$,所以 $\triangle APQ$ 与 $\triangle ABC$ 的面积的比值为 $\frac{S_{\triangle APQ}}{S_{\triangle ABC}}=\frac{PQ}{BC}=\frac{5}{12}$.
9. 已知点$O$是$\triangle ABC$的内心,若$\overrightarrow{AO}=\frac{3}{7}\overrightarrow{AB}+\frac{1}{7}\overrightarrow{AC}$,则$\cos\angle BAC=$
$\frac{1}{6}$
。
答案:
9.$\frac{1}{6}$[解析]如图,取 $AB$ 的中点 $D$,连接 $OB$,$OC$,$OD$. 因为 $-\overrightarrow{OA}=\frac{3}{7}(\overrightarrow{OB}-\overrightarrow{OA})+\frac{1}{7}(\overrightarrow{OC}-\overrightarrow{OA})$,即 $\overrightarrow{OC}=-3(\overrightarrow{OA}+\overrightarrow{OB})=-6\overrightarrow{OD}$,所以点 $C$,$O$,$D$ 共线. 又 $\angle ACO=\angle BCO$,所以 $AC=BC$,且 $CD\perp AB$,所以 $\cos\angle BAC=\frac{AD}{AC}$. 又由 $OA$ 为 $\angle BAC$ 的平分线可知 $\frac{AD}{AC}=\frac{OD}{OC}=\frac{1}{6}$,即 $\cos\angle BAC=\frac{1}{6}$.
9.$\frac{1}{6}$[解析]如图,取 $AB$ 的中点 $D$,连接 $OB$,$OC$,$OD$. 因为 $-\overrightarrow{OA}=\frac{3}{7}(\overrightarrow{OB}-\overrightarrow{OA})+\frac{1}{7}(\overrightarrow{OC}-\overrightarrow{OA})$,即 $\overrightarrow{OC}=-3(\overrightarrow{OA}+\overrightarrow{OB})=-6\overrightarrow{OD}$,所以点 $C$,$O$,$D$ 共线. 又 $\angle ACO=\angle BCO$,所以 $AC=BC$,且 $CD\perp AB$,所以 $\cos\angle BAC=\frac{AD}{AC}$. 又由 $OA$ 为 $\angle BAC$ 的平分线可知 $\frac{AD}{AC}=\frac{OD}{OC}=\frac{1}{6}$,即 $\cos\angle BAC=\frac{1}{6}$.

10. [2024·银川一中月考]已知$P,Q$是$\triangle ABC$所在平面内的两个定点,且满足$\overrightarrow{PA}+\overrightarrow{PC}=\boldsymbol{0}$,$2\overrightarrow{QA}+\overrightarrow{QB}+\overrightarrow{QC}=\overrightarrow{BC}$。若$|\overrightarrow{PQ}|=\lambda|\overrightarrow{BC}|$,则实数$\lambda=$
$\frac{1}{2}$
。
答案:
10.$\frac{1}{2}$[解析]由 $\overrightarrow{PA}+\overrightarrow{PC}=0$,知 $\overrightarrow{PA}=-\overrightarrow{PC}=\overrightarrow{CP}$,所以 $P$ 是边 $AC$ 的中点. 因为 $2\overrightarrow{QA}+\overrightarrow{QB}+\overrightarrow{QC}=\overrightarrow{BC}$,所以 $2\overrightarrow{QA}=\overrightarrow{BC}-\overrightarrow{QB}-\overrightarrow{QC}=\overrightarrow{BC}+\overrightarrow{CQ}+\overrightarrow{BQ}=2\overrightarrow{BQ}$,从而有 $\overrightarrow{QA}=\overrightarrow{BQ}$,故 $Q$ 是边 $AB$ 的中点,所以 $PQ$ 是 $\triangle ABC$ 的中位线,所以 $|\overrightarrow{PQ}|=\frac{1}{2}|\overrightarrow{BC}|$,故 $\lambda=\frac{1}{2}$.
11. [2024·鞍山一中月考]如图,在$\triangle ABC$中,点$O$在$BC$边上,且$\overrightarrow{BO}=2\overrightarrow{OC}$,过点$O$的直线与直线$AB,AC$分别交于$M,N$两点($M,N$不与点$B,C$重合),若$\overrightarrow{AM}=m\overrightarrow{AB}$,$\overrightarrow{AN}=n\overrightarrow{AC}$,则$\frac{mn}{2m+n}=$

$\frac{1}{3}$
。
答案:
11.$\frac{1}{3}$[解析]由 $\overrightarrow{BO}=2\overrightarrow{OC}$,得 $\overrightarrow{AO}-\overrightarrow{AB}=2(\overrightarrow{AC}-\overrightarrow{AO})$,即 $\overrightarrow{AO}=\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$. 因为 $M$,$O$,$N$ 三点共线,设 $\overrightarrow{MO}=\lambda\overrightarrow{ON}$,则 $\overrightarrow{AO}-\overrightarrow{AM}=\lambda(\overrightarrow{AN}-\overrightarrow{AO})$,整理可得 $(\lambda+1)\overrightarrow{AO}=m\overrightarrow{AB}+\lambda n\overrightarrow{AC}$,即 $\frac{m}{m+1}\overrightarrow{AB}+\frac{\lambda n}{\lambda+1}\overrightarrow{AC}=\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$,即 $(\frac{m}{m+1}-\frac{1}{3})\overrightarrow{AB}+(\frac{\lambda n}{\lambda+1}-\frac{2}{3})\overrightarrow{AC}=0$. 因为 $\overrightarrow{AB}$,$\overrightarrow{AC}$ 不共线,所以 $\begin{cases}\frac{m}{m+1}-\frac{1}{3}=0,\frac{\lambda n}{\lambda+1}-\frac{2}{3}=0,\end{cases}$ 所以 $\frac{1}{3m}+\frac{2}{3n}=0$,所以 $\frac{1}{3m}+\frac{\lambda}{\lambda+1}=1$,则 $\frac{1}{m}+\frac{2}{n}=3$,即 $\frac{n+2m}{mn}=3$,所以 $\frac{n}{2m+n}=\frac{1}{3}$.
12. [2024·信阳高中月考]已知$O$是线段$AB$外一点,若$\overrightarrow{OA}=\boldsymbol{a}$,$\overrightarrow{OB}=\boldsymbol{b}$。
(1)如图1,设点$G$是$\triangle OAB$的重心,求证:$\overrightarrow{OG}=\frac{1}{3}(\boldsymbol{a}+\boldsymbol{b})$;
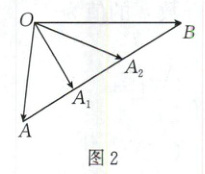
(2)如图2,设$A_1,A_2$是线段$AB$的三等分点,$\triangle OAA_1,\triangle OA_1A_2$及$\triangle OA_2B$的重心依次为$G_1,G_2,G_3$,试用向量$\boldsymbol{a},\boldsymbol{b}$表示$\overrightarrow{OG_1}+\overrightarrow{OG_2}+\overrightarrow{OG_3}$;
(3)如果在线段$AB$上有若干个等分点,请你写出一个正确的结论。(不必证明)
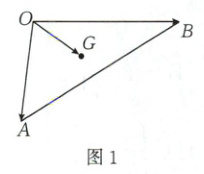
(1)如图1,设点$G$是$\triangle OAB$的重心,求证:$\overrightarrow{OG}=\frac{1}{3}(\boldsymbol{a}+\boldsymbol{b})$;
(2)如图2,设$A_1,A_2$是线段$AB$的三等分点,$\triangle OAA_1,\triangle OA_1A_2$及$\triangle OA_2B$的重心依次为$G_1,G_2,G_3$,试用向量$\boldsymbol{a},\boldsymbol{b}$表示$\overrightarrow{OG_1}+\overrightarrow{OG_2}+\overrightarrow{OG_3}$;
(3)如果在线段$AB$上有若干个等分点,请你写出一个正确的结论。(不必证明)


答案:
12.
(1)证明:延长 $OG$ 交 $AB$ 于点 $E$ (图略),易知 $E$ 为 $AB$ 的中点,则 $\overrightarrow{OG}=\frac{2}{3}\overrightarrow{OE}=\frac{2}{3}×\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})=\frac{1}{3}(\overrightarrow{a}+\overrightarrow{b})$.
(2)因为 $G_1$,$G_2$,$G_3$ 分别是 $\triangle OAA_1$,$\triangle OA_1A_2$,$\triangle OA_2B$ 的重心,所以 $\overrightarrow{OG_1}=\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OA_1})$,$\overrightarrow{OG_2}=\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OA_2})$,$\overrightarrow{OG_3}=\frac{1}{3}(\overrightarrow{OA_2}+\overrightarrow{OB})$. 又 $A_1$,$A_2$ 是线段 $AB$ 的三等分点,所以 $\overrightarrow{OG_1}+\overrightarrow{OG_2}+\overrightarrow{OG_3}=\frac{1}{3}(\overrightarrow{a}+\overrightarrow{b})+\frac{2}{3}[\overrightarrow{a}+\frac{1}{3}(\overrightarrow{b}-\overrightarrow{a})+\overrightarrow{a}+\frac{2}{3}(\overrightarrow{b}-\overrightarrow{a})]=\overrightarrow{a}+\overrightarrow{b}$.
(3)结论一:设 $A_1$,$A_2$,$·s$,$A_{n - 1}$ 是线段 $AB$ 的 $n$ 等分点,则 $\overrightarrow{OA_k}+\overrightarrow{OA_{n - k}}=\overrightarrow{a}+\overrightarrow{b}(k = 1,2,·s,n - 1)$. 结论二:设 $A_1$,$A_2$,$·s$,$A_{n - 1}$ 是线段 $AB$ 的 $n$ 等分点,则 $\overrightarrow{OA_1}+\overrightarrow{OA_2}+·s+\overrightarrow{OA_{n - 1}}=\frac{n - 1}{2}(\overrightarrow{a}+\overrightarrow{b})$. 结论三:设 $A_1$,$A_2$,$·s$,$A_{n - 1}$ 是线段 $AB$ 的 $n$ 等分点,$G_1$,$G_2$,$·s$,$G_n$ 分别是 $\triangle OAA_1$,$\triangle OA_1A_2$,$·s$,$\triangle OA_{n - 1}B$ 的重心,则 $\overrightarrow{OG_1}+\overrightarrow{OG_2}+·s+\overrightarrow{OG_n}=\frac{n}{3}(\overrightarrow{a}+\overrightarrow{b})$.(给出其中之一即可)
(1)证明:延长 $OG$ 交 $AB$ 于点 $E$ (图略),易知 $E$ 为 $AB$ 的中点,则 $\overrightarrow{OG}=\frac{2}{3}\overrightarrow{OE}=\frac{2}{3}×\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})=\frac{1}{3}(\overrightarrow{a}+\overrightarrow{b})$.
(2)因为 $G_1$,$G_2$,$G_3$ 分别是 $\triangle OAA_1$,$\triangle OA_1A_2$,$\triangle OA_2B$ 的重心,所以 $\overrightarrow{OG_1}=\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OA_1})$,$\overrightarrow{OG_2}=\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OA_2})$,$\overrightarrow{OG_3}=\frac{1}{3}(\overrightarrow{OA_2}+\overrightarrow{OB})$. 又 $A_1$,$A_2$ 是线段 $AB$ 的三等分点,所以 $\overrightarrow{OG_1}+\overrightarrow{OG_2}+\overrightarrow{OG_3}=\frac{1}{3}(\overrightarrow{a}+\overrightarrow{b})+\frac{2}{3}[\overrightarrow{a}+\frac{1}{3}(\overrightarrow{b}-\overrightarrow{a})+\overrightarrow{a}+\frac{2}{3}(\overrightarrow{b}-\overrightarrow{a})]=\overrightarrow{a}+\overrightarrow{b}$.
(3)结论一:设 $A_1$,$A_2$,$·s$,$A_{n - 1}$ 是线段 $AB$ 的 $n$ 等分点,则 $\overrightarrow{OA_k}+\overrightarrow{OA_{n - k}}=\overrightarrow{a}+\overrightarrow{b}(k = 1,2,·s,n - 1)$. 结论二:设 $A_1$,$A_2$,$·s$,$A_{n - 1}$ 是线段 $AB$ 的 $n$ 等分点,则 $\overrightarrow{OA_1}+\overrightarrow{OA_2}+·s+\overrightarrow{OA_{n - 1}}=\frac{n - 1}{2}(\overrightarrow{a}+\overrightarrow{b})$. 结论三:设 $A_1$,$A_2$,$·s$,$A_{n - 1}$ 是线段 $AB$ 的 $n$ 等分点,$G_1$,$G_2$,$·s$,$G_n$ 分别是 $\triangle OAA_1$,$\triangle OA_1A_2$,$·s$,$\triangle OA_{n - 1}B$ 的重心,则 $\overrightarrow{OG_1}+\overrightarrow{OG_2}+·s+\overrightarrow{OG_n}=\frac{n}{3}(\overrightarrow{a}+\overrightarrow{b})$.(给出其中之一即可)
查看更多完整答案,请扫码查看


