《2025年热搜题高中数学必修第二册人教版》

10. [2024·莆田七中期中](多选)已知 $a// b$，$|a| = 2|b| = 8$，则 $|a + b|$ 的值可能为 (AD)

A.4
B.8
C.10
D.12

答案： 10.AD 【解析】由$a// b$可知$a,b$共线，由$\vert\boldsymbol{a}\vert=2\vert\boldsymbol{b}\vert=8$可得$\vert\boldsymbol{a}\vert=8,\vert\boldsymbol{b}\vert=4$. 当$a,b$方向相同时，$\vert\boldsymbol{a}+\boldsymbol{b}\vert=\vert\boldsymbol{a}\vert+\vert\boldsymbol{b}\vert=12$，当$a,b$方向相反时，$\vert\boldsymbol{a}+\boldsymbol{b}\vert=\vert\boldsymbol{a}\vert-\vert\boldsymbol{b}\vert=4$. 故选AD.

11. [2024·张家口一中期中]给出下列不等式或等式：
①$|a| - |b| ＜ |a + b| ＜ |a| + |b|$；
②$|a| - |b| = |a + b| = |a| + |b|$；
③$|a| - |b| = |a + b| ＜ |a| + |b|$；
④$|a| - |b| ＜ |a + b| = |a| + |b|$.
其中，一定不成立的个数是 (A)

A.0
B.1
C.2
D.3

答案： 11.A 【解析】①当$a$与$b$不共线时成立；②当$b=\boldsymbol{0}$时成立；③当$a$与$b$共线，方向相反，且$\vert\boldsymbol{a}\vert\geqslant\vert\boldsymbol{b}\vert$时成立；④当$a$与$b$共线，且方向相同时成立. 故选A.

12. [2024·山东师大附中月考](多选)已知 $a$，$b$ 为非零向量，则下列命题中正确的有 (BD)

A.若 $||a| - |b|| = |a + b|$，则 $a$ 与 $b$ 方向相同
B.若 $|a| + |b| = |a - b|$，则 $a$ 与 $b$ 方向相反
C.若 $|a| + |b| = |a - b|$，则 $a$ 与 $b$ 有相等的模
D.若 $||a| - |b|| = |a - b|$，则 $a$ 与 $b$ 方向相同

答案： 12.BD 【解析】当$a,b$方向相同时，有$\vert\boldsymbol{a}\vert+\vert\boldsymbol{b}\vert=\vert\boldsymbol{a}+\boldsymbol{b}\vert$，$\vert\boldsymbol{a}\vert-\vert\boldsymbol{b}\vert=\vert\boldsymbol{a}-\boldsymbol{b}\vert$；当$a,b$方向相反时，有$\vert\vert\boldsymbol{a}\vert-\vert\boldsymbol{b}\vert\vert=\vert\boldsymbol{a}-\boldsymbol{b}\vert$,$\vert\boldsymbol{a}\vert+\vert\boldsymbol{b}\vert=\vert\boldsymbol{a}-\boldsymbol{b}\vert$. 因此B,D正确.

13. [2024·郑州一中期中]设 $|a| = 8$，$|b| = 12$，求 $|a + b|$ 的取值范围.

答案： 13.当$a,b$同向共线时，$\vert\boldsymbol{a}+\boldsymbol{b}\vert=\vert\boldsymbol{a}\vert+\vert\boldsymbol{b}\vert=8 + 12 = 20$；当$a,b$反向共线时，$\vert\boldsymbol{a}+\boldsymbol{b}\vert=\vert\vert\boldsymbol{a}\vert-\vert\boldsymbol{b}\vert\vert=4$；当$a,b$不共线时，$\vert\vert\boldsymbol{a}\vert-\vert\boldsymbol{b}\vert\vert＜\vert\boldsymbol{a}+\boldsymbol{b}\vert＜\vert\boldsymbol{a}\vert+\vert\boldsymbol{b}\vert$，即$4＜\vert\boldsymbol{a}+\boldsymbol{b}\vert＜20$，所以$\vert\boldsymbol{a}+\boldsymbol{b}\vert$的取值范围是$[4,20]$.

1. [2024·宁波镇海中学期中](多选)已知 $D$，$E$，$F$ 分别是 $\triangle ABC$ 的边 $AB$，$BC$，$AC$ 的中点，则下列等式中正确的有 (ABC)

A.$\overrightarrow{FD}+\overrightarrow{DA}=\overrightarrow{FA}$
B.$\overrightarrow{FD}+\overrightarrow{DE}+\overrightarrow{EF}=0$
C.$\overrightarrow{DE}+\overrightarrow{DA}=\overrightarrow{EC}$
D.$\overrightarrow{DA}+\overrightarrow{DE}=\overrightarrow{FD}$

答案： 1.ABC 【解析】对于A,$\overrightarrow{FD}+\overrightarrow{DA}=\overrightarrow{FA}$,故A正确；对于B,$\overrightarrow{FD}+\overrightarrow{DE}+\overrightarrow{EF}=\overrightarrow{FE}+\overrightarrow{EF}=\boldsymbol{0}$,故B正确；对于C,根据向量加法的平行四边形法则可知$\overrightarrow{DE}+\overrightarrow{DA}=\overrightarrow{DF}=\overrightarrow{EC}$,故C正确；对于D,$\overrightarrow{DA}+\overrightarrow{DE}=\overrightarrow{DF}\neq\overrightarrow{FD}$,故D错误. 故选ABC.

2. [2024·南京金陵中学期中](多选)已知 $\overrightarrow{OD}+\overrightarrow{OE}=\overrightarrow{OM}$，则下列结论正确的有 (BCD)

A.$\overrightarrow{OD}+\overrightarrow{EO}=\overrightarrow{OM}$
B.$\overrightarrow{OM}+\overrightarrow{DO}=\overrightarrow{OE}$
C.$\overrightarrow{OM}-\overrightarrow{OE}=\overrightarrow{OD}$
D.$\overrightarrow{DO}+\overrightarrow{EO}=\overrightarrow{MO}$

答案： 2.BCD 【解析】由已知得，四边形ODME为平行四边形. 对于A,$\overrightarrow{OD}+\overrightarrow{EO}=\overrightarrow{ED}$,故A错误；对于B,$\overrightarrow{OM}+\overrightarrow{DO}=\overrightarrow{OM}-\overrightarrow{OD}=\overrightarrow{DM}=\overrightarrow{OE}$,故B正确；对于C,由$\overrightarrow{OD}+\overrightarrow{OE}=\overrightarrow{OM}$得$\overrightarrow{OM}-\overrightarrow{OE}=\overrightarrow{OD}$,故C正确；对于D,由$\overrightarrow{OD}+\overrightarrow{OE}=\overrightarrow{OM}$得$-\overrightarrow{OD}-\overrightarrow{OE}=-\overrightarrow{OM}$,即$\overrightarrow{DO}+\overrightarrow{EO}=\overrightarrow{MO}$,故D正确. 故选BCD.

3. [2024·山东省实验中学期中]已知 $P$ 是 $\triangle ABC$ 所在平面内一点，且满足 $\overrightarrow{PA}+\overrightarrow{PB}=\overrightarrow{PC}$，则下列结论正确的是 (D)

A.点 $P$ 在 $\triangle ABC$ 的内部
B.点 $P$ 在 $\triangle ABC$ 的边 $AB$ 上
C.点 $P$ 在 $AB$ 边所在的直线上
D.点 $P$ 在 $\triangle ABC$ 的外部

答案： 3.D 【解析】由$\overrightarrow{PA}+\overrightarrow{PB}=\overrightarrow{PC}$,可得$\overrightarrow{PA}=\overrightarrow{PC}-\overrightarrow{PB}=\overrightarrow{BC}$,所以四边形PBCA为平行四边形，所以点P在$\triangle ABC$的外部.

4. [2024·重庆巴蜀中学月考]已知 $O$ 为四边形 $ABCD$ 所在平面内的一点，且向量 $\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$，$\overrightarrow{OD}$ 满足等式 $\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}$，若 $E$ 为 $AC$ 的中点，则 $\frac{S_{\triangle EAB}}{S_{\triangle BCD}}=$ (B)

A.$\frac{1}{4}$
B.$\frac{1}{2}$
C.$\frac{1}{3}$
D.$\frac{2}{3}$

答案： 4.B 【解析】因为向量$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC},\overrightarrow{OD}$满足等式$\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}$,所以$\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{OD}-\overrightarrow{OC}$,即$\overrightarrow{BA}=\overrightarrow{CD}$,则四边形ABCD为平行四边形. 因为E为AC的中点，所以E为对角线AC与BD的交点，则$S_{\triangle EAB}=S_{\triangle ECD}=S_{\triangle ADE}=S_{\triangle BCE}$,则$\frac{S_{\triangle EAB}}{S_{\triangle BCD}}=\frac{1}{2}$. 故选B.

5. [2024·咸宁调考]在中心为 $O$ 的正八边形 $A_1A_2·s A_8$ 中，$a_0=\overrightarrow{A_8A_1}$，$a_i=\overrightarrow{A_iA_{i + 1}}(i = 1,2,·s,7)$，$b_j=\overrightarrow{OA_j}(j = 1,2,·s,8)$，则 $a_2 + a_5 + b_2 + b_5 + b_7=$ (D)

A.$a_3$
B.$b_3$
C.$a_6$
D.$b_6$

答案：
5.D 【解析】如图，因为$\overrightarrow{OA_3}+\overrightarrow{OA_7}=0$,所以$a_3 + a_7 = b_5 + b_7 = A_2\overrightarrow{A_3}+A_5\overrightarrow{A_6}+ \overrightarrow{OA_5}+\overrightarrow{OA_6}+\overrightarrow{OA_7}=( \overrightarrow{OA_2}+A_2\overrightarrow{A_3})+( \overrightarrow{OA_5}+A_5\overrightarrow{A_6})+\overrightarrow{OA_7}=\overrightarrow{OA_3}+\overrightarrow{OA_6}+\overrightarrow{OA_7}=\overrightarrow{OA_6}=b_6$. 故选D.

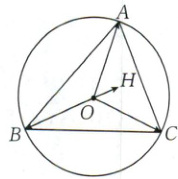
6. [2024·武汉二中月考]如图，$O$ 为 $\triangle ABC$ 的外心，$H$ 为其垂心，则下列结论一定成立的是 (A)


A.$\overrightarrow{AH}=\overrightarrow{OB}+\overrightarrow{OC}$
B.$\overrightarrow{BH}=\overrightarrow{AC}$
C.$\overrightarrow{HC}=\overrightarrow{BA}$
D.$\overrightarrow{OH}=\overrightarrow{OA}-\overrightarrow{OB}+\overrightarrow{OC}$

答案：
6.A 【解析】如图，连接AH,HC,延长BO交圆O于点D，连接DA,DC，则$OB = OD,DA\perp AB,DC\perp BC$. 又$AH\perp BC,CH\perp AB$,所以$CH// DA,AH// DC$,所以四边形AHCD是平行四边形，所以$\overrightarrow{AH}=\overrightarrow{DC}$. 又$\overrightarrow{DC}=\overrightarrow{OC}-\overrightarrow{OD}=\overrightarrow{OC}+\overrightarrow{OB}$,所以$\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{AH}=\overrightarrow{OA}+\overrightarrow{DC}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$,即$\overrightarrow{OH}-\overrightarrow{OA}=\overrightarrow{OB}+\overrightarrow{OC}$,所以$\overrightarrow{AH}=\overrightarrow{OB}+\overrightarrow{OC}$. 故选A.