2025年热搜题高中数学必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年热搜题高中数学必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
5. [2024·淮南二中月考]轴截面为正方形的圆柱的外接球的体积与该圆柱的体积的比值为(
A.$\frac{4}{3}$
B.$\frac{3}{2}$
C.$\frac{4\sqrt{2}}{3}$
D.$2\sqrt{2}$
C
)A.$\frac{4}{3}$
B.$\frac{3}{2}$
C.$\frac{4\sqrt{2}}{3}$
D.$2\sqrt{2}$
答案:
5.C[解析]设圆柱的底面半径为R,则圆柱的高为2R,圆柱的体积V = πR²·2R = 2πR³.圆柱外接球的半径为$\sqrt{2}$R,体积为$\frac{4}{3}$π($\sqrt{2}$R)³ = $\frac{8\sqrt{2}}{3}$πR³,故外接球的体积与该圆柱的体积的比值为$\frac{\frac{8\sqrt{2}}{3}πR³}{2πR³}$ = $\frac{4\sqrt{2}}{3}$.故选C.
6. [2024·中山一中期末]若等边三角形 $ABC$ 的边长为 $2$,将它沿高 $AD$ 翻折,使点 $B$ 与点 $C$ 间的距离为 $\sqrt{2}$,则此时四面体 $A - BCD$ 外接球的表面积为(
A.$\frac{5\sqrt{5}}{6}\pi$
B.$\frac{7\sqrt{7}}{6}\pi$
C.$5\pi$
D.$7\pi$
C
)A.$\frac{5\sqrt{5}}{6}\pi$
B.$\frac{7\sqrt{7}}{6}\pi$
C.$5\pi$
D.$7\pi$
答案:
6.C[解析]由题意作图,如图1所示,由于等边三角形三线合一,则BD = CD = 1.因为翻折后BC = $\sqrt{2}$,所以翻折后BD⊥CD,则四面体A - BCD的外接球与以BD,CD,AD为棱的长方体的外接球相同,如图2所示.长方体外接球的半径R = $\frac{1}{2}$$\sqrt{BD² + CD² + AD²}$ = $\frac{1}{2}$×$\sqrt{1² + 1² + (\sqrt{3})²}$ = $\frac{\sqrt{5}}{2}$,所以四面体A - BCD外接球的表面积为4πR² = 5π.
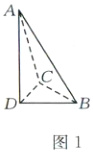

6.C[解析]由题意作图,如图1所示,由于等边三角形三线合一,则BD = CD = 1.因为翻折后BC = $\sqrt{2}$,所以翻折后BD⊥CD,则四面体A - BCD的外接球与以BD,CD,AD为棱的长方体的外接球相同,如图2所示.长方体外接球的半径R = $\frac{1}{2}$$\sqrt{BD² + CD² + AD²}$ = $\frac{1}{2}$×$\sqrt{1² + 1² + (\sqrt{3})²}$ = $\frac{\sqrt{5}}{2}$,所以四面体A - BCD外接球的表面积为4πR² = 5π.


7. [2024·西安中学月考](多选)已知某正方体的外接球上有一个动点 $M$,该正方体的内切球上有一个动点 $N$,若线段 $MN$ 的最小值为 $\sqrt{3} - 1$,则下列说法正确的有(
A.正方体的外接球的表面积为 $12\pi$
B.正方体的内切球的体积为 $\frac{4\pi}{3}$
C.正方体的棱长为 $2$
D.线段 $MN$ 的最大值为 $2\sqrt{3}$
ABC
)A.正方体的外接球的表面积为 $12\pi$
B.正方体的内切球的体积为 $\frac{4\pi}{3}$
C.正方体的棱长为 $2$
D.线段 $MN$ 的最大值为 $2\sqrt{3}$
答案:
7.ABC[解析]设正方体的棱长为a,则正方体外接球半径为体对角线长的一半,为$\frac{\sqrt{3}}{2}$a,内切球半径为棱长的一半,为$\frac{a}{2}$.因为M,N分别为该正方体外接球和内切球上的动点,所以MNmin = $\frac{\sqrt{3}}{2}$a - $\frac{a}{2}$ = $\frac{\sqrt{3} - 1}{2}$a = $\sqrt{3}$ - 1,解得a = 2,所以正方体的棱长为2,C正确.正方体的外接球的表面积为4π×($\sqrt{3}$)² = 12π,A正确.正方体的内切球的体积为$\frac{4}{3}$π×1³ = $\frac{4π}{3}$,B正确.线段MN的最大值为$\frac{\sqrt{3}}{2}$a + $\frac{a}{2}$ = $\sqrt{3}$ + 1,D错误.故选ABC.
8. [2024·长春质检]有一倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为 $r$ 的铁球,并注入水,使水面与球正好相切,然后将球取出,这时容器中水的深度为
$\sqrt[3]{15}$r
.
答案:
8.$\sqrt[3]{15}$r[解析]由题意知,圆锥的轴截面为正三角形,如图所示.根据切线性质知,当球在容器内时,水深为3r,水面的半径为$\sqrt{3}$r,则容器内水的体积为V = V圆锥 - V球 = $\frac{1}{3}$π·($\sqrt{3}$r)²·3r - $\frac{4}{3}$πr³ = $\frac{5}{3}$πr³,而将球取出后,设容器内水的深度为h,则水面圆的半径为$\frac{\sqrt{3}}{3}$h,从而容器内水的体积是V′ = $\frac{1}{3}$π·($\frac{\sqrt{3}}{3}$h)²·h = $\frac{1}{9}$πh³,由V = V′,得h = $\sqrt[3]{15}$r.即容器中水的深度为$\sqrt[3]{15}$r.

8.$\sqrt[3]{15}$r[解析]由题意知,圆锥的轴截面为正三角形,如图所示.根据切线性质知,当球在容器内时,水深为3r,水面的半径为$\sqrt{3}$r,则容器内水的体积为V = V圆锥 - V球 = $\frac{1}{3}$π·($\sqrt{3}$r)²·3r - $\frac{4}{3}$πr³ = $\frac{5}{3}$πr³,而将球取出后,设容器内水的深度为h,则水面圆的半径为$\frac{\sqrt{3}}{3}$h,从而容器内水的体积是V′ = $\frac{1}{3}$π·($\frac{\sqrt{3}}{3}$h)²·h = $\frac{1}{9}$πh³,由V = V′,得h = $\sqrt[3]{15}$r.即容器中水的深度为$\sqrt[3]{15}$r.

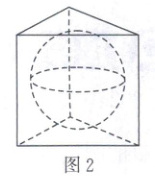
9. [2024·天津一中月考]天津滨海新区文化中心地处天津滨海新区开发区,是天津乃至京津冀地区的标志性文化工程.其中滨海图书馆建筑独具特色,被称为“滨海之眼”,如图 1 所示.为了测量馆中球的半径,小明设计了两个方案.方案甲:构造正三棱柱,其侧面均与球相切,底面边长约为 $30$ m,如图 2 所示,估计此时球的完整表面积为

300π
$m^2$;方案乙:测得球被地面截得的圆的周长约为 $16\pi$ m,地面到球顶部高度约为 $16$ m,估计此时球的完整体积为$\frac{4000π}{3}$
$m^3$.

答案:
9.300π $\frac{4000π}{3}$[解析]方案甲:过球心作与正三棱柱底面平行的截面,如图1,则BM = $\frac{1}{2}$BC = 15(m),∠OBM = $\frac{π}{6}$,所以tan∠OBM = tan$\frac{π}{6}$ = $\frac{OM}{BM}$ = $\frac{\sqrt{3}}{3}$,即球的半径R = OM = $\frac{\sqrt{3}}{3}$×15 = 5$\sqrt{3}$(m),所以S = 4πR² = 300π(m²).
方案乙:由周长可得截面圆半径r = $\frac{16π}{2π}$ = 8(m),过球心作垂直于地面的截面,如图2,由直角三角形可得(16 - R)² + r² = R²,解得R = 10m,所以V = $\frac{4}{3}$πR³ = $\frac{4000π}{3}$(m³).
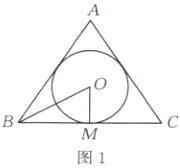

9.300π $\frac{4000π}{3}$[解析]方案甲:过球心作与正三棱柱底面平行的截面,如图1,则BM = $\frac{1}{2}$BC = 15(m),∠OBM = $\frac{π}{6}$,所以tan∠OBM = tan$\frac{π}{6}$ = $\frac{OM}{BM}$ = $\frac{\sqrt{3}}{3}$,即球的半径R = OM = $\frac{\sqrt{3}}{3}$×15 = 5$\sqrt{3}$(m),所以S = 4πR² = 300π(m²).
方案乙:由周长可得截面圆半径r = $\frac{16π}{2π}$ = 8(m),过球心作垂直于地面的截面,如图2,由直角三角形可得(16 - R)² + r² = R²,解得R = 10m,所以V = $\frac{4}{3}$πR³ = $\frac{4000π}{3}$(m³).


10. 已知点 $A$,$B$,$C$,$D$ 均在球 $O$ 上,$AB = BC = \sqrt{3}$,$AC = 3$,若三棱锥 $D - ABC$ 体积的最大值为 $\frac{3\sqrt{3}}{4}$,则球 $O$ 的表面积为(
A.$36\pi$
B.$16\pi$
C.$12\pi$
D.$\frac{16}{3}\pi$
B
)A.$36\pi$
B.$16\pi$
C.$12\pi$
D.$\frac{16}{3}\pi$
答案:
10.B[解析]由题意可得,∠ABC = 120°,△ABC的外接圆半径r = $\sqrt{3}$,当三棱锥的体积取最大值时,V三棱锥D - ABC = $\frac{1}{3}$S△ABC·h,即$\frac{3\sqrt{3}}{4}$ = $\frac{1}{3}$×$\frac{3\sqrt{3}}{4}$h,解得h = 3.设R为球O的半径,则(3 - R)² = R² - r²,解得R = 2.故球O的表面积为4π×2² = 16π.
11. [2024·湘潭一中月考]已知底面半径为 $3$ 的圆锥 $SO$($S$ 为顶点,$O$ 为底面圆心)的体积为 $12\pi$.若球 $O_1$ 在圆锥 $SO$ 内,则球 $O_1$ 的表面积的最大值为(
A.$9\pi$
B.$\frac{9\pi}{2}$
C.$\frac{32\pi}{3}$
D.$12\pi$
A
)A.$9\pi$
B.$\frac{9\pi}{2}$
C.$\frac{32\pi}{3}$
D.$12\pi$
答案:
11.A[解析]如图所示,圆锥SO的轴截面为等腰三角形SAB,因为底面半径为3,所以底面积为9π.又因为圆锥SO的体积为12π,所以圆锥的高h = $\frac{3×12π}{9π}$ = 4,母线长为$\sqrt{3² + 4²}$ = 5.当球O₁的表面积最大时,球O₁的轴截面是△SAB的内切圆,设球O₁的半径为r,所以S△SAB = $\frac{1}{2}$AB·h = $\frac{1}{2}$(SA + SB + AB)·r,解得r = $\frac{3}{2}$,所以球O₁的表面积的最大值为4π×($\frac{3}{2}$)² = 9π.故选A.

11.A[解析]如图所示,圆锥SO的轴截面为等腰三角形SAB,因为底面半径为3,所以底面积为9π.又因为圆锥SO的体积为12π,所以圆锥的高h = $\frac{3×12π}{9π}$ = 4,母线长为$\sqrt{3² + 4²}$ = 5.当球O₁的表面积最大时,球O₁的轴截面是△SAB的内切圆,设球O₁的半径为r,所以S△SAB = $\frac{1}{2}$AB·h = $\frac{1}{2}$(SA + SB + AB)·r,解得r = $\frac{3}{2}$,所以球O₁的表面积的最大值为4π×($\frac{3}{2}$)² = 9π.故选A.

12. [2024·哈尔滨三中月考]粽子,古时在北方也称“角黍”,是由粽叶包裹糯米、黍米等馅料蒸煮制成的食品,是中国汉族传统节庆食物之一,端午食粽的风俗,千百年来在中国盛行不衰.粽子形状多样,馅料种类繁多,南北方风味各有不同.某四角蛋黄粽可近似看成一个正四面体,蛋黄近似看成一个球体,且每个粽子里仅包裹一个蛋黄,若粽子的棱长为 $9$ cm,则其内可包裹的蛋黄的最大体积约为(参考数据:$\sqrt{6} \approx 2.45$,$\pi \approx 3.14$)(
A.$20$ cm³
B.$22$ cm³
C.$26$ cm³
D.$30$ cm³
C
)A.$20$ cm³
B.$22$ cm³
C.$26$ cm³
D.$30$ cm³
答案:
12.C[解析]当粽子内包裹的蛋黄与粽子内切时,该粽子内可包裹的蛋黄体积最大.如图,正四面体D - ABC,其内切球O与底面ABC切于O₁,设内切球半径为r,连接DO₁,则O在DO₁上,连接OA,OB,OC,连接BO₁并延长交AC于F,易知O₁为△ABC的中心,F为边AC的中点.易得BF = $\frac{\sqrt{3}}{2}$×9 = $\frac{9\sqrt{3}}{2}$(cm),则S△ABC = $\frac{81\sqrt{3}}{4}$cm²,BO₁ = $\frac{2}{3}$BF = 3$\sqrt{3}$cm,所以DO₁ = $\sqrt{BD² - BO₁²}$ = 3$\sqrt{6}$cm,所以V三棱锥D - ABC = $\frac{1}{3}$·S△ABC·DO₁ = $\frac{243\sqrt{2}}{4}$cm³.因为V三棱锥D - ABC = V三棱锥O - ABC + V三棱锥O - BCD + V三棱锥O - ABD + V三棱锥O - ACD = 4V三棱锥O - ABC = 4×$\frac{1}{3}$×$\frac{81\sqrt{3}}{4}$×r = 27$\sqrt{3}$r(cm³),所以27$\sqrt{3}$r = $\frac{243\sqrt{2}}{4}$,解得r = $\frac{3\sqrt{6}}{4}$cm,所以球O的体积V = $\frac{4}{3}$π·($\frac{3\sqrt{6}}{4}$)³ = $\frac{27\sqrt{6}}{8}$π ≈ $\frac{27}{8}$×2.45×3.14 ≈ 26(cm³).

12.C[解析]当粽子内包裹的蛋黄与粽子内切时,该粽子内可包裹的蛋黄体积最大.如图,正四面体D - ABC,其内切球O与底面ABC切于O₁,设内切球半径为r,连接DO₁,则O在DO₁上,连接OA,OB,OC,连接BO₁并延长交AC于F,易知O₁为△ABC的中心,F为边AC的中点.易得BF = $\frac{\sqrt{3}}{2}$×9 = $\frac{9\sqrt{3}}{2}$(cm),则S△ABC = $\frac{81\sqrt{3}}{4}$cm²,BO₁ = $\frac{2}{3}$BF = 3$\sqrt{3}$cm,所以DO₁ = $\sqrt{BD² - BO₁²}$ = 3$\sqrt{6}$cm,所以V三棱锥D - ABC = $\frac{1}{3}$·S△ABC·DO₁ = $\frac{243\sqrt{2}}{4}$cm³.因为V三棱锥D - ABC = V三棱锥O - ABC + V三棱锥O - BCD + V三棱锥O - ABD + V三棱锥O - ACD = 4V三棱锥O - ABC = 4×$\frac{1}{3}$×$\frac{81\sqrt{3}}{4}$×r = 27$\sqrt{3}$r(cm³),所以27$\sqrt{3}$r = $\frac{243\sqrt{2}}{4}$,解得r = $\frac{3\sqrt{6}}{4}$cm,所以球O的体积V = $\frac{4}{3}$π·($\frac{3\sqrt{6}}{4}$)³ = $\frac{27\sqrt{6}}{8}$π ≈ $\frac{27}{8}$×2.45×3.14 ≈ 26(cm³).

13. [2024·佳木斯一中期中]已知一圆锥 $SO$($S$ 为顶点,$O$ 为底面圆心)的底面直径为 $3$,高为 $\frac{3\sqrt{3}}{2}$,在该圆锥内放置一个棱长为 $a$ 的正四面体,并且正四面体在该圆锥内可以任意转动,则该正四面体的表面积的最大值为
2$\sqrt{3}$
.
答案:
13.2$\sqrt{3}$[解析]依题意,正四面体可以在圆锥内任意转动,则当该正四面体内接于圆锥的内切球时,a最大,设内切球的球心为P,半径为r,圆锥底面半径为R,轴截面上球与圆锥母线的切点为Q,圆锥的轴截面如图1所示.则OA = OB = R = $\frac{3}{2}$,OS = $\frac{3\sqrt{3}}{2}$,所以tan∠SAO = $\sqrt{3}$,则△SAB为等边三角形,故P是△SAB的中心.连接BP,则BP平分∠SBA,所以∠PBO = 30°,所以tan30° = $\frac{r}{R}$,即r = $\frac{\sqrt{3}}{3}$R = $\frac{\sqrt{3}}{2}$.即正四面体的外接球的半径为$\frac{\sqrt{3}}{2}$.将正四面体放在正方体中,如图2所示.则正四面体D - M₁NC₁的外接球即为正方体MNCD - M₁N₁C₁D₁的外接球,从图中可以得到,当正四面体的棱长为a时,正方体的棱长为$\frac{\sqrt{2}}{2}$a,则2r = $\sqrt{3}$×$\frac{\sqrt{2}}{2}$a,所以a最大 = $\frac{2\sqrt{6}}{3}$r = $\frac{2\sqrt{6}}{3}$×$\frac{\sqrt{3}}{2}$ = $\sqrt{2}$.所以正四面体的表面积的最大值为4×$\frac{\sqrt{3}}{4}$×($\sqrt{2}$)² = 2$\sqrt{3}$.
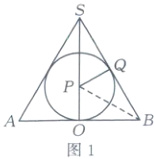

13.2$\sqrt{3}$[解析]依题意,正四面体可以在圆锥内任意转动,则当该正四面体内接于圆锥的内切球时,a最大,设内切球的球心为P,半径为r,圆锥底面半径为R,轴截面上球与圆锥母线的切点为Q,圆锥的轴截面如图1所示.则OA = OB = R = $\frac{3}{2}$,OS = $\frac{3\sqrt{3}}{2}$,所以tan∠SAO = $\sqrt{3}$,则△SAB为等边三角形,故P是△SAB的中心.连接BP,则BP平分∠SBA,所以∠PBO = 30°,所以tan30° = $\frac{r}{R}$,即r = $\frac{\sqrt{3}}{3}$R = $\frac{\sqrt{3}}{2}$.即正四面体的外接球的半径为$\frac{\sqrt{3}}{2}$.将正四面体放在正方体中,如图2所示.则正四面体D - M₁NC₁的外接球即为正方体MNCD - M₁N₁C₁D₁的外接球,从图中可以得到,当正四面体的棱长为a时,正方体的棱长为$\frac{\sqrt{2}}{2}$a,则2r = $\sqrt{3}$×$\frac{\sqrt{2}}{2}$a,所以a最大 = $\frac{2\sqrt{6}}{3}$r = $\frac{2\sqrt{6}}{3}$×$\frac{\sqrt{3}}{2}$ = $\sqrt{2}$.所以正四面体的表面积的最大值为4×$\frac{\sqrt{3}}{4}$×($\sqrt{2}$)² = 2$\sqrt{3}$.


查看更多完整答案,请扫码查看


