《2025年热搜题高中数学必修第二册人教版》

5. [2024·六安调研]已知非零向量$\overrightarrow{AB}$与$\overrightarrow{AC}$满足$(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}+\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|})·\overrightarrow{BC}=0$，且$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}·\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}=\frac{1}{2}$，则△ABC是(D)

A.三边均不相等的三角形
B.直角三角形
C.等腰三角形
D.等边三角形

答案： 5.D [解析]由$(\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|} + \frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}) · \overrightarrow{BC} = 0$，得$\angle BAC$的平分线垂直于$BC$，所以$AB = AC$. 因为$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|} · \frac{\overrightarrow{AC}}{|\overrightarrow{AC}|} = \frac{\overrightarrow{AB} · \overrightarrow{AC}}{|\overrightarrow{AB}| · |\overrightarrow{AC}|} = \frac{1}{2}$，$0° ＜ \langle\overrightarrow{AB}, \overrightarrow{AC}\rangle ＜ 180°$，所以$\angle BAC = 60°$，所以$\triangle ABC$为等边三角形. 故选D.

6. [2024·乐山一中月考]在△ABC中，若$\overrightarrow{BC}=\boldsymbol{a}$，$\overrightarrow{CA}=\boldsymbol{b}$，$\overrightarrow{AB}=\boldsymbol{c}$，且$\boldsymbol{a}·\boldsymbol{b}=\boldsymbol{b}·\boldsymbol{c}=\boldsymbol{c}·\boldsymbol{a}$，则△ABC为(A)

A.等边三角形
B.直角三角形
C.等腰三角形
D.以上都不对

答案：
6.A [解析]因为$\mathbf{a} · \mathbf{b} = |\mathbf{a}| · |\mathbf{b}| · \cos(\pi - C) = -|\mathbf{a}| · |\mathbf{b}| \cos C$，$\mathbf{b} · \mathbf{c} = |\mathbf{b}| · |\mathbf{c}| \cos(\pi - A) = -|\mathbf{b}| · |\mathbf{c}| \cos A$，$\mathbf{c} · \mathbf{a} = |\mathbf{c}| · |\mathbf{a}| \cos(\pi - B) = -|\mathbf{c}| · |\mathbf{a}| \cos B$，且$\mathbf{a} · \mathbf{b} = \mathbf{b} · \mathbf{c} = \mathbf{c} · \mathbf{a}$，所以$-|\mathbf{a}| · |\mathbf{b}| \cos C = -|\mathbf{c}| · |\mathbf{a}| \cos A = -|\mathbf{b}| · |\mathbf{c}| \cos B$，所以$|\mathbf{a}| \cos C = |\mathbf{c}| \cos A$，$|\mathbf{b}| \cos A = |\mathbf{a}| \cos B$，所以$A$，$B$，$C$均为锐角. 如图所示. 作$BD \perp AC$于点$D$，则$|\overrightarrow{CD}| = |\mathbf{a}| \cos C$，$|\overrightarrow{AD}| = |\mathbf{c}| \cos A$，所以$|\overrightarrow{CD}| = |\overrightarrow{AD}|$，所以$D$为边$AC$的中点，所以$|\overrightarrow{AB}| = |\overrightarrow{BC}|$. 同理可证$|\overrightarrow{AB}| = |\overrightarrow{AC}|$，所以$\triangle ABC$为等边三角形.

7. [2024·荆门一中月考]设P是△ABC所在平面内的一点，若$\overrightarrow{AB}·(\overrightarrow{CB}+\overrightarrow{CA})=2\overrightarrow{AB}·\overrightarrow{CP}$，且$\overrightarrow{AB}^{2}=\overrightarrow{AC}^{2}-2\overrightarrow{BC}·\overrightarrow{AP}$，则点P是△ABC的(A)

A.外心
B.内心
C.重心
D.垂心

答案： 7.A [解析]由$\overrightarrow{AB} · (\overrightarrow{CB} + \overrightarrow{CA}) = 2\overrightarrow{AB} · \overrightarrow{CP}$，得$\overrightarrow{AB} · (\overrightarrow{CB} + \overrightarrow{CA} - 2\overrightarrow{CP}) = 0$，即$\overrightarrow{AB} · [(\overrightarrow{CB} - \overrightarrow{CP}) + (\overrightarrow{CA} - \overrightarrow{CP})] = 0$，所以$\overrightarrow{AB} · (\overrightarrow{PB} + \overrightarrow{PA}) = 0$. 设$D$为$AB$的中点，则$\overrightarrow{AB} · 2\overrightarrow{PD} = 0$，故$\overrightarrow{AB} · \overrightarrow{PD} = 0$. 因为$\overrightarrow{AB^2} = \overrightarrow{AC^2} - 2\overrightarrow{BC} · \overrightarrow{AP}$，所以$(\overrightarrow{AC} + \overrightarrow{AB})(\overrightarrow{AC} - \overrightarrow{AB}) = 2\overrightarrow{BC} · \overrightarrow{AP}$，所以$\overrightarrow{BC} · (\overrightarrow{AC} + \overrightarrow{AB} - 2\overrightarrow{AP}) = 0$. 设$BC$的中点为$E$，同上可知$\overrightarrow{BC} · \overrightarrow{PE} = 0$，所以$P$为$AB$与$BC$的垂直平分线的交点，所以$P$是$\triangle ABC$的外心.

8. 如图所示，过△ABC内部(含边界)一点M任作一条直线EF，作$AD\perp EF$于点D，$BE\perp EF$于点E，$CF\perp EF$于点F。若$\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\boldsymbol{0}$，则点M是△ABC的(B)

A.三条高的交点
B.三条中线的交点
C.三边中垂线的交点
D.三个内角平分线的交点

答案： 8.B [解析]根据特殊位置法，可以判断，当直线$EF$经过$C$点时，$\overrightarrow{AD} + \overrightarrow{BE} + \overrightarrow{CF} = 0$，即$\overrightarrow{AD} + \overrightarrow{BE} = 0$，于是$|\overrightarrow{AD}| = |\overrightarrow{BE}|$，$\overrightarrow{EF}$即为$AB$边上的中线. 同理，当$EF$经过$A$点时，$EF$是$BC$边上的中线，当$EF$经过$B$点时，$EF$是$AC$边上的中线. 因此，$M$是$\triangle ABC$的三条中线的交点. 故选B.

9. [2024·日照一中期中]若点O在△ABC内，且满足$2\overrightarrow{BA}-6\overrightarrow{BC}+9\overrightarrow{OC}=\boldsymbol{0}$，设$S_{\triangle BOC}$为△BOC的面积，$S_{\triangle ABC}$为△ABC的面积，则$\frac{S_{\triangle BOC}}{S_{\triangle ABC}}=$$\frac{2}{9}$。

答案：
9.$\frac{2}{9}$ [解析]由$2\overrightarrow{BA} - 6\overrightarrow{BC} + 9\overrightarrow{OC} = 0$，可得$2(\overrightarrow{OA} - \overrightarrow{OB}) - 6(\overrightarrow{OC} - \overrightarrow{OB}) + 9\overrightarrow{OC} = 2\overrightarrow{OA} + 4\overrightarrow{OB} + 3\overrightarrow{OC} = 0$. 延长$OA$，$OB$，$OC$，使$OD = 2OA$，$OE = 4OB$，$OF = 3OC$，如图所示，因为$2\overrightarrow{OA} + 4\overrightarrow{OB} + 3\overrightarrow{OC} = 0$，所以$\overrightarrow{OD} + \overrightarrow{OE} + \overrightarrow{OF} = 0$，即$O$是$\triangle DEF$的重心，故$\triangle DOE$，$\triangle EOF$，$\triangle DOF$的面积相等，不妨令它们的面积均为$1$，则$\triangle AOB$的面积为$\frac{1}{8}$，$\triangle BOC$的面积为$\frac{1}{12}$，$\triangle AOC$的面积为$\frac{1}{6}$，故$\triangle AOB$，$\triangle BOC$，$\triangle AOC$的面积之比为$\frac{1}{8} : \frac{1}{12} : \frac{1}{6} = 3 : 2 : 4$，所以$\frac{S_{\triangle BOC}}{S_{\triangle ABC}} = \frac{2}{9}$.

10. [2024·重庆一中月考]如图所示，在△ABC中，点D在边BC上，且$\overrightarrow{DC}=2\overrightarrow{BD}$。
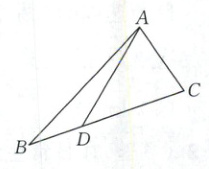
（1）用向量$\overrightarrow{AB}$，$\overrightarrow{AC}$表示向量$\overrightarrow{AD}$；
（2）若$|\overrightarrow{AB}|:|\overrightarrow{AD}|:|\overrightarrow{AC}| = 3:k:1$，求实数k的取值范围。

答案： 10.
(1)已知点$D$在边$BC$上，且$\overrightarrow{DC} = 2\overrightarrow{BD}$，所以$\overrightarrow{AC} - \overrightarrow{AD} = 2(\overrightarrow{AD} - \overrightarrow{AB})$. 整理得$\overrightarrow{AD} = \frac{2}{3}\overrightarrow{AB} + \frac{1}{3}\overrightarrow{AC}$.
(2)根据$|\overrightarrow{AB}| : |\overrightarrow{AD}| : |\overrightarrow{AC}| = 3 : k : 1$，设$|\overrightarrow{AB}| = 3t$，$|\overrightarrow{AD}| = kt$，$|\overrightarrow{AC}| = t$ ($t ＞ 0$)，由$\overrightarrow{AD} = \frac{2}{3}\overrightarrow{AB} + \frac{1}{3}\overrightarrow{AC}$，得$\overrightarrow{AD^2} = \frac{4}{9}\overrightarrow{AB^2} + \frac{4}{9}\overrightarrow{AB} · \overrightarrow{AC} + \frac{1}{9}\overrightarrow{AC^2}$，所以$k^2t^2 = \frac{4}{9} × 9t^2 + \frac{4}{9} × 3t^2 × \cos\angle BAC + \frac{t^2}{9}$，即$k^2 = \frac{37}{9} + \frac{4}{3}\cos\angle BAC$. 因为$0 ＜ \angle BAC ＜ \pi$，所以$-1 ＜ \cos\angle BAC ＜ 1$. 所以解得$\frac{5}{3} ＜ k ＜ \frac{7}{3}$.

11. [2024·泉州调研]如图所示，设$\overrightarrow{AB}=\boldsymbol{a}$，$\overrightarrow{AD}=\boldsymbol{b}$，E，F分别是平行四边形ABCD的边AD，CD的中点，BE，BF分别与对角线AC交于点R和T，利用向量法证明$AR = RT = TC$。

答案： 11.证明：由题意知$\mathbf{a}$，$\mathbf{b}$不共线，$\overrightarrow{AR} // \overrightarrow{AC}$，可设$\overrightarrow{AR} = \lambda\overrightarrow{AC}$ ($\lambda \in \mathbf{R}$)，即$\overrightarrow{AR} = \lambda(\mathbf{a} + \mathbf{b}) = \lambda\mathbf{a} + \lambda\mathbf{b}$. 因为$E$为$AD$的中点，所以$\overrightarrow{AE} = \frac{1}{2}\overrightarrow{AD} = \frac{1}{2}\mathbf{b}$. 由$\overrightarrow{ER} // \overrightarrow{EB}$，可设$\overrightarrow{ER} = k\overrightarrow{EB}$ ($k \in \mathbf{R}$)，所以$\overrightarrow{ER} = k(\mathbf{a} - \frac{1}{2}\mathbf{b})$，所以$\overrightarrow{AR} = \overrightarrow{AE} + \overrightarrow{ER} = \frac{1}{2}\mathbf{b} + k(\mathbf{a} - \frac{1}{2}\mathbf{b}) = k\mathbf{a} + \frac{1 - k}{2}\mathbf{b}$. 由①②得$\begin{cases} \lambda - k = 0, \\ \lambda + \frac{k - 1}{2} = 0, \end{cases}$因为$\mathbf{a}$，$\mathbf{b}$不共线，所以$\begin{cases} \lambda - k = 0, \\ \lambda + \frac{k - 1}{2} = 0, \end{cases}$解得$\lambda = \frac{1}{3}$，所以$\overrightarrow{AR} = \frac{1}{3}\overrightarrow{AC}$，即$\overrightarrow{AR} = \frac{1}{3}\overrightarrow{AC}$. 同理可得$\overrightarrow{TC} = \frac{1}{3}\overrightarrow{AC}$，即$\overrightarrow{TC} = \frac{1}{3}\overrightarrow{AC}$. 所以$RT = \frac{1}{3}AC$. 故$AR = RT = TC$.