《2025年热搜题高中数学必修第二册人教版》

1. 给出下列三个命题：①若$\vert a\vert = 0$，则$a = 0$；②若$\vert a\vert = \vert b\vert$，则$a = b$或$a = -b$；③若$a// b$，则$\vert a\vert = \vert b\vert$。其中正确的命题有(A)

A.0 个
B.1 个
C.2 个
D.3 个

答案： 1.A【解析】①忽略了0与0的区别，$a = 0$；②混淆了两个向量的模相等和两个实数的绝对值相等，两个向量的模相等，只能说明它们的长度相等，它们的方向并不确定；③两个向量平行，可以得出它们的方向相同或相反，未必能得出它们的模相等.所以正确的命题有0个.

2. [2024·南京金陵中学周练](多选)下列叙述中错误的有(ABCD)

A.若$a = b$，则$3a ＞ 2b$
B.若$a// b$，则$a$与$b$的方向相同或相反
C.若$a// b$，$b// c$，则$a// c$
D.对任一向量$a$，$\frac{a}{\vert a\vert}$是一个单位向量

答案： 2.ABCD【解析】向量不能比较大小，故A错误；由于零向量与任一向量共线，且零向量的方向是任意的，故B错误；对于C，若$\boldsymbol{b}$为零向量，$\boldsymbol{a}$与$\boldsymbol{c}$可能不是共线向量，故C错误；对于D，当$a = 0$时，$\frac {a}{|a|}$无意义，故D错误.
易错警示
平行向量不具有传递性，即$a// b,b// c \nRightarrow a// c$，因为当$b$为零向量时，无法得到$a// c$.

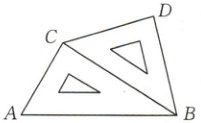
3. [2024·厦门双十中学期中]将一副三角板中的两个直角三角板按如图所示的位置摆放，若$BC = 8\sqrt{3}$，则$\overrightarrow{AC}·\overrightarrow{DB} =$(B)


A.$-96$
B.$-32\sqrt{3}$
C.$32\sqrt{3}$
D.$96$

答案： 3.B【解析】由题意可得$AC = BC\tan30^{\circ}=8\sqrt{3}×\frac{\sqrt{3}}{3}=8$，
$CD = BC\cos45^{\circ}=8\sqrt{3}×\frac{\sqrt{2}}{2}=4\sqrt{6}$.因为$AC\perp CB$，$\angle ACD = 135^{\circ}$，所以$\overrightarrow{AC}·\overrightarrow{DB}=\overrightarrow{AC}·(\overrightarrow{CB}-\overrightarrow{CD})=\overrightarrow{AC}·\overrightarrow{CB}-\overrightarrow{AC}·\overrightarrow{CD}=0 - |\overrightarrow{AC}|·|\overrightarrow{CD}|·\cos(180^{\circ}-\angle ACD)= - 8×4\sqrt{6}×\frac{\sqrt{2}}{2}=-32\sqrt{3}$.故选B.
易错警示
求向量的夹角时两向量要共起点，注意本题中向量$\overrightarrow{AC},\overrightarrow{CD}$的夹角不是$135^{\circ}$，而是$45^{\circ}$.

4. [2024·威海一中期中]设两个向量$e_1$，$e_2$满足$\vert e_1\vert = 2$，$\vert e_2\vert = 1$，$e_1$，$e_2$的夹角为$60^{\circ}$。若向量$2e_1 + 7e_2$与$e_1 + te_2$的夹角为钝角，则实数$t$的取值范围为$(-7,-\frac{\sqrt{14}}{2})\cup(-\frac{\sqrt{14}}{2},-\frac{1}{2})$。

答案： 4.$(-7,-\frac{\sqrt{14}}{2})\cup(-\frac{\sqrt{14}}{2},-\frac{1}{2})$【解析】由向量$2t\boldsymbol{e_1}+7\boldsymbol{e_2}$与$\boldsymbol{e_1}+t\boldsymbol{e_2}$的夹角为钝角，得$\frac{(2t\boldsymbol{e_1}+7\boldsymbol{e_2})·(\boldsymbol{e_1}+t\boldsymbol{e_2})}{|2t\boldsymbol{e_1}+7\boldsymbol{e_2}||\boldsymbol{e_1}+t\boldsymbol{e_2}|}＜0$，即$(2t\boldsymbol{e_1}+7\boldsymbol{e_2})·(\boldsymbol{e_1}+t\boldsymbol{e_2})＜0$.
整理，得$2t\boldsymbol{e_1}^{2}+(2t^{2}+7)\boldsymbol{e_1}·\boldsymbol{e_2}+7t\boldsymbol{e_2}^{2}＜0$.①
因为$|\boldsymbol{e_1}| = 2,|\boldsymbol{e_2}| = 1,\langle\boldsymbol{e_1},\boldsymbol{e_2}\rangle = 60^{\circ}$，所以$\boldsymbol{e_1}·\boldsymbol{e_2}=2×1×\cos60^{\circ}=1$.
所以①式化简，得$2t^{2}+15t + 7＜0$，解得$-7＜t＜-\frac{1}{2}$.
当$2t\boldsymbol{e_1}+7\boldsymbol{e_2}$与$\boldsymbol{e_1}+t\boldsymbol{e_2}$的夹角为$180^{\circ}$时，
设$2t\boldsymbol{e_1}+7\boldsymbol{e_2}=\lambda(\boldsymbol{e_1}+t\boldsymbol{e_2})(\lambda＜0)$.
所以$\begin{cases}2t=\lambda,\\7=\lambda t,\end{cases}$解得$\begin{cases}\lambda=-\sqrt{14},\\t=-\frac{\sqrt{14}}{2}.\end{cases}$故实数$t$的取值范围是$(-7,-\frac{\sqrt{14}}{2})\cup(-\frac{\sqrt{14}}{2},-\frac{1}{2})$.
易错警示
在求解时，忽略$2t\boldsymbol{e_1}+7\boldsymbol{e_2}$与$\boldsymbol{e_1}+t\boldsymbol{e_2}$共线的情形而致误，出现错误的原因是误认为$a· b＜0$与$\langle a,b\rangle$为钝角等价.

5. [2024·武汉中学期中]已知$a = (1,2)$，$b = (1,1)$，且$a$与$a + \lambda b$的夹角为锐角，则实数$\lambda$的取值范围为$(-\frac{5}{3},0)\cup(0,+\infty)$。

答案： 5.$(-\frac{5}{3},0)\cup(0,+\infty)$【解析】因为$\boldsymbol{a}$与$\boldsymbol{a}+\lambda\boldsymbol{b}$均为非零向量，且夹角为锐角，所以$\boldsymbol{a}·(\boldsymbol{a}+\lambda\boldsymbol{b})＞0$，即$(1,2)·(1+\lambda,2+\lambda)＞0$，所以$(1+\lambda)+2(2+\lambda)＞0$，所以$\lambda＞-\frac{5}{3}$.当$\boldsymbol{a}$与$\boldsymbol{a}+\lambda\boldsymbol{b}$共线时，存在实数$m$，使$\boldsymbol{a}+\lambda\boldsymbol{b}=m\boldsymbol{a}$，即$(1+\lambda,2+\lambda)=m(1,2)$，所以$\begin{cases}1+\lambda=m,\\2+\lambda=2m,\end{cases}$所以$\lambda = 0$，即当$\lambda = 0$时，$\boldsymbol{a}$与$\boldsymbol{a}+\lambda\boldsymbol{b}$共线.综上可知，实数$\lambda$的取值范围为$(-\frac{5}{3},0)\cup(0,+\infty)$.
易错警示
此处在求解时，容易忽略$\boldsymbol{a}$与$\boldsymbol{a}+\lambda\boldsymbol{b}$共线的情形而致误，出现错误的原因是误认为$a· b＞0$与$\langle a,b\rangle$为锐角等价，而事实上，$a· b＞0$并不等价于$a,b$的夹角为锐角，$a· b＞0$等价于$a$与$b$夹角为锐角或$0^{\circ}$.

6. 已知$\triangle ABC$的三条边的长度分别为 4 米、5 米、6 米，将三边都截掉$x$米后，剩余的部分组成一个钝角三角形，则$x$的取值范围是(C)

A.$(0,5)$
B.$(1,5)$
C.$(1,3)$
D.$(1,4)$

答案： 6.C【解析】根据题意，将三边都截掉$x$米后，三角形的三边长分别为$(4 - x)$米、$(5 - x)$米、$(6 - x)$米，且$0＜x＜4$.设长为$(6 - x)$米的边所对的角为$\alpha$，则$\alpha$为钝角.因为$4 - x＞0,5 - x＞0,6 - x＞0,\cos\alpha=\frac{(4 - x)^{2}+(5 - x)^{2}-(6 - x)^{2}}{2(4 - x)(5 - x)}＜0$，所以$1＜x＜4$.因为$4 - x + 5 - x＞6 - x$，所以$x＜3$，所以$1＜x＜3$，故$x$的取值范围是$(1,3)$.故选C.
易错警示
若要长度分别为$4 - x,5 - x,6 - x$的线段构成三角形，需要满足$4 - x + 5 - x＞6 - x$（两边之和大于第三边），忽视构成三角形的条件是出错的主要原因.

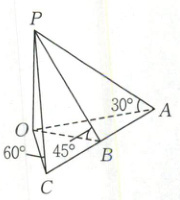
7. 如图所示，在地面上共线的三点$A$，$B$，$C$处测得一建筑物的仰角分别为$30^{\circ}$，$45^{\circ}$，$60^{\circ}$，且$AB = BC = 60m$，则建筑物的高度为(D)


A.$15\sqrt{6}m$
B.$20\sqrt{6}m$
C.$25\sqrt{6}m$
D.$30\sqrt{6}m$

答案： 7.D【解析】设建筑物的高度为$h$m.由题图知，$PA = 2h$，$PB=\sqrt{2}h$，$PC=\frac{2\sqrt{3}}{3}h$.在$\triangle PBA$和$\triangle PBC$中，由余弦定理的推论得，$\cos\angle PBA=\frac{60^{2}+2h^{2}-4h^{2}}{2×60×\sqrt{2}h}$①，
$\cos\angle PBC=\frac{60^{2}+2h^{2}-\frac{4}{3}h^{2}}{2×60×\sqrt{2}h}$②.
因为$\angle PBA+\angle PBC = 180^{\circ}$，所以$\cos\angle PBA+\cos\angle PBC = 0$③.
由①②③，解得$h = 30\sqrt{6}$或$h=-30\sqrt{6}$(舍去).即建筑物的高度为$30\sqrt{6}$m.

8. [2024·郑州一中月考]学校里有一棵树，甲同学在$A$地测得树尖$D$的仰角为$45^{\circ}$，乙同学在$B$地测得树尖$D$的仰角为$30^{\circ}$，量得$AB = AC = 10m$，树根部为$C$($A$，$B$，$C$在同一水平面上)，则$\angle ACB =$$30^{\circ}$。

答案：
8.$30^{\circ}$【解析】如图所示，在$Rt\triangle ACD$中，因为$AC = 10$m，$\angle DAC = 45^{\circ}$，所以$DC = 10$m.在$Rt\triangle DCB$中，因为$\angle DBC = 30^{\circ}$，所以$BC = 10\sqrt{3}$m.在$\triangle ABC$中，$\cos\angle ACB=\frac{10^{2}+(10\sqrt{3})^{2}-10^{2}}{2×10×10\sqrt{3}}=\frac{\sqrt{3}}{2}$.
因为$\angle ACB\in(0,180^{\circ})$，所以$\angle ACB = 30^{\circ}$.
易错警示
依据题意正确画出“立体图形”是求解的关键.本题易误认为点$A,B,C,D$在同一平面内，进而出现无法求解的情况.

9. [2024·昆明三中月考]在不等边三角形$ABC$中，$a$为最大边，若$a^2 ＜ b^2 + c^2$，则$A$的取值范围是$\{A|60^{\circ}＜A＜90^{\circ}\}$。

答案： 9.$\{A|60^{\circ}＜A＜90^{\circ}\}$【解析】因为$a^{2}＜b^{2}+c^{2}$，所以$b^{2}+c^{2}-a^{2}＞0$，则$\cos A=\frac{b^{2}+c^{2}-a^{2}}{2bc}＞0$，所以$A＜90^{\circ}$.又因为$a$为最大边，所以$A＞60^{\circ}$.故$A$的取值范围是$\{A|60^{\circ}＜A＜90^{\circ}\}$.

10. 在$\triangle ABC$中，内角$A$，$B$，$C$所对的边分别为$a$，$b$，$c$。若$2\cos^2\frac{A}{2} = \frac{\sqrt{3}}{3}\sin A$，$a = 2\sqrt{3}$，则$\triangle ABC$周长的取值范围为$(4\sqrt{3},4 + 2\sqrt{3}]$。

答案： 10.$(4\sqrt{3},4 + 2\sqrt{3}]$【解析】由$2\cos^{2}\frac{A}{2}=\frac{\sqrt{3}}{3}\sin A + 1$得$1+\cos A=\frac{\sqrt{3}}{3}\sin A$，即$\frac{\sqrt{3}}{3}\sin A-\cos A = 1$，所以$\frac{2\sqrt{3}}{3}\sin(A-\frac{\pi}{3}) = 1$，即$\sin(A-\frac{\pi}{3})=\frac{\sqrt{3}}{2}$.因为$0＜A＜\pi$，所以$-\frac{\pi}{3}＜A-\frac{\pi}{3}＜\frac{2\pi}{3}$，所以$A-\frac{\pi}{3}=\frac{\pi}{3}$，即$A=\frac{2\pi}{3}$.因为$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=\frac{2\sqrt{3}}{\sqrt{3}} = 4$，所以$b = 4\sin B$，$c = 4\sin C$.则$b + c = 4\sin B + 4\sin(\frac{\pi}{3}-B)=4\sin B + 4(\frac{\sqrt{3}}{2}\cos B-\frac{1}{2}\sin B)=2\sin B + 2\sqrt{3}\cos B = 4\sin(B+\frac{\pi}{3})$.
因为$0＜B＜\frac{\pi}{3}$，所以$\frac{\pi}{3}＜B+\frac{\pi}{3}＜\frac{2\pi}{3}$.
所以$\frac{\sqrt{3}}{2}＜\sin(B+\frac{\pi}{3})\leq1$，即$2\sqrt{3}＜4\sin(B+\frac{\pi}{3})\leq4$，所以$2\sqrt{3}＜b + c\leq4$，则$4\sqrt{3}＜a + b + c\leq4 + 2\sqrt{3}$，即$\triangle ABC$的周长的取值范围是$(4\sqrt{3},4 + 2\sqrt{3}]$.
易错警示
本题求解的易错之处是在根据正弦定理将$b + c$转化为$4\sin(B+\frac{\pi}{3})$时，忽视$0＜B＜\frac{\pi}{3}$而误认为$0＜B＜\pi$出现错误.事实上，$A=\frac{2\pi}{3}$，因此$C + B=\frac{\pi}{3}$，从而可得$0＜B＜\frac{\pi}{3}$，因此涉及三角形内角的范围时，若已知其他角的值，应注意用来缩小所求角的范围.

11. [2024·宜春一中期中]已知在$\triangle ABC$中，内角$A$，$B$，$C$所对的边分别为$a$，$b$，$c$。若$a = \sqrt{3}$，$b = \sqrt{2}$，$B = 45^{\circ}$，求角$A$，$C$和边$c$。

答案： 11.由正弦定理$\frac{a}{\sin A}=\frac{b}{\sin B}$，得$\sin A=\frac{\sqrt{3}}{2}$.
因为$a＞b$，所以$A = 60^{\circ}$或$A = 120^{\circ}$.当$A = 60^{\circ}$时，$C = 180^{\circ}-45^{\circ}-60^{\circ}=75^{\circ}$，$c=\frac{b\sin C}{\sin B}=\frac{\sqrt{6}+\sqrt{2}}{2}$.当$A = 120^{\circ}$时，$C = 180^{\circ}-45^{\circ}-120^{\circ}=15^{\circ}$，$c=\frac{b\sin C}{\sin B}=\frac{\sqrt{6}-\sqrt{2}}{2}$.
易错警示
上述解法中，用正弦定理求$C$时，由$\sin A=\frac{\sqrt{3}}{2}$可得$A = 60^{\circ}$或$A = 120^{\circ}$，故$C = 75^{\circ}$或$C = 15^{\circ}$.解题时易漏解而造成错误.