2025年热搜题高中数学必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年热搜题高中数学必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. [2024·温州中学期中]在△ABC中,c/b = cosC/cosB,则△ABC为(
A.直角三角形
B.等腰直角三角形
C.等腰三角形
D.等腰或直角三角形
C
)A.直角三角形
B.等腰直角三角形
C.等腰三角形
D.等腰或直角三角形
答案:
1.C【解析】由$\frac{c}{b}=\frac{\cos C}{\cos B}$,知$\frac{c}{b}=\frac{\frac{a^{2}+b^{2}-c^{2}}{2ab}}{\frac{c^{2}+a^{2}-b^{2}}{2ca}}$,化简得$b=c$,所以$\triangle ABC$为等腰三角形.
2. [2024·深圳中学月考]在△ABC中,若(a + b + c)(a - b + c) = 3ac,且2acosC = b,则△ABC为(
A.等边三角形
B.等腰三角形
C.直角三角形
D.无法判断
A
)A.等边三角形
B.等腰三角形
C.直角三角形
D.无法判断
答案:
2.A【解析】由$(a+b+c)(a-b+c)=3ac$,得$c^{2}+a^{2}-b^{2}=ac$,于是$\cos B=\frac{c^{2}+a^{2}-b^{2}}{2ca}=\frac{1}{2}$,故$B=60°$.又由$2a\cos C=b$,得$2× a×\frac{a^{2}+b^{2}-c^{2}}{2ab}=b$,所以$a=c$,故$\triangle ABC$是等边三角形.
3. [2024·新乡一中月考]在△ABC中,三边上的高依次为1/13,1/5,1/11,则△ABC为(
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不存在这样的三角形
C
)A.锐角三角形
B.直角三角形
C.钝角三角形
D.不存在这样的三角形
答案:
3.C【解析】设$\triangle ABC$的内角A,B,C所对的边分别为$a$,$b$,$c$,且$\frac{1}{13},\frac{1}{5},\frac{1}{11}$分别为$a$,$b$,$c$上的高.因为$S_{\triangle ABC}=\frac{1}{2}a×\frac{1}{13}=\frac{1}{2}b×\frac{1}{5}=\frac{1}{2}c×\frac{1}{11}$,所以可设$a=13k,b=5k,c=11k(k>0)$.由余弦定理的推论,得$\cos A=\frac{(5k)^{2}+(11k)^{2}-(13k)^{2}}{2×5k×11k}=\frac{23}{110}<0$,则$A\in(\frac{\pi}{2},\pi)$,所以$\triangle ABC$为钝角三角形.故选C.
4. [2024·东营一中月考](多选)在△ABC中,若acosA = bcosB,则△ABC可能为(
A.直角三角形
B.等腰三角形
C.钝角三角形
D.等边三角形
AB
)A.直角三角形
B.等腰三角形
C.钝角三角形
D.等边三角形
答案:
4.AB【解析】将余弦定理的推论代入条件$a\cos A=b\cos B$中,得$a·\frac{b^{2}+c^{2}-a^{2}}{2bc}=b·\frac{c^{2}+a^{2}-b^{2}}{2ca}$,化简得$a^{2}(b^{2}+c^{2}-a^{2})=b^{2}(c^{2}+a^{2}-b^{2})$,即$(a^{2}-b^{2})(a^{2}+b^{2}-c^{2})=0$,所以$a=b$或$a^{2}+b^{2}=c^{2}$至少有一个式子成立.故选AB.
5. [2024·成都七中期中]在△ABC中,acosA + bcosB = ccosC,试判断△ABC的形状.
答案:
5.将余弦定理的推论$\cos A=\frac{b^{2}+c^{2}-a^{2}}{2bc}$,$\cos B=\frac{c^{2}+a^{2}-b^{2}}{2ca}$,$\cos C=\frac{a^{2}+b^{2}-c^{2}}{2ab}$,代入等式$a\cos A+b\cos B=c\cos C$中,得$a·\frac{b^{2}+c^{2}-a^{2}}{2bc}+b·\frac{c^{2}+a^{2}-b^{2}}{2ca}=c·\frac{a^{2}+b^{2}-c^{2}}{2ab}$两边同乘$2abc$,得$a^{2}(b^{2}+c^{2}-a^{2})+b^{2}(c^{2}+a^{2}-b^{2})=c^{2}(a^{2}+b^{2}-c^{2})$,所以$a^{4}+b^{4}-2a^{2}b^{2}=c^{4}$,所以$(a^{2}-b^{2})^{2}=c^{4}$,所以$a^{2}-b^{2}=c^{2}$或$a^{2}-b^{2}=-c^{2}$,所以$a^{2}=b^{2}+c^{2}$或$b^{2}=a^{2}+c^{2}$,所以$\triangle ABC$是以A或B为直角的直角三角形.
6. 已知△ABC三个内角A,B,C的对边分别为a,b,c.若c/(a + b) + a/(b + c) = 1,则B = (
A.30°
B.60°
C.120°
D.150°
B
)A.30°
B.60°
C.120°
D.150°
答案:
6.B【解析】由$\frac{c}{a+b}+\frac{a}{b+c}=1$整理可得$c^{2}+a^{2}-b^{2}=ac$.所以由余弦定理的推论可得$\cos B=\frac{c^{2}+a^{2}-b^{2}}{2ca}=\frac{ac}{2ca}=\frac{1}{2}$.因为$0°<B<180°$,所以$B=60°$.故选B.
7. [2024·深圳宝安中学期末]在△ABC中,已知C = π/3,BC = a,AC = b,且a,b是方程x² - 13x + 40 = 0的两根,则AB = (
A.2
B.4
C.6
D.7
D
)A.2
B.4
C.6
D.7
答案:
7.D【解析】因为$a$,$b$是方程$x^{2}-13x+40=0$的两根,所以$a=5,b=8$或$a=8,b=5$.由余弦定理得$AB^{2}=a^{2}+b^{2}-2ab\cos C=25+64-2×8×5×\frac{1}{2}=49$,所以$AB=7$.
8. P是△ABC所在平面内一点,当PA + PB + PC取得最小值时,称该点为△ABC的“费马点”.当△ABC的三个内角均小于120°时,“费马点”满足如下特征:∠APB = ∠BPC = ∠CPA = 120°.如图,在△ABC中,AB = AC = √7,BC = √3,则其“费马点”P到A,B,C三点的距离之和为(
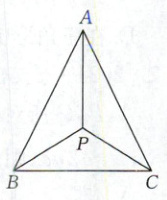
A.4
B.2
C.2 - 2√3
D.2 + √3
A
)
A.4
B.2
C.2 - 2√3
D.2 + √3
答案:
8.A【解析】根据题意,得$\triangle ABC$为等腰三角形,因为$\angle APB=\angle APC=\angle BPC=120°$,所以$PB=PC$.在$\triangle PBC$中,由余弦定理,得$BC^{2}=BP^{2}+CP^{2}-2BP· CP·\cos\angle BPC$,即$(\sqrt{3})^{2}=2BP^{2}-2×(-\frac{1}{2})BP^{2}$,解得$BP=1$.在$\triangle ABP$中,由余弦定理,得$AB^{2}=BP^{2}+AP^{2}-2BP· AP·\cos\angle APB$,即$(\sqrt{7})^{2}=1+AP^{2}-2×(-\frac{1}{2})AP$,所以$AP=2$,所以$AP+BP+CP=4$,所以“费马点”P到A,B,C三点的距离之和为4.故选A.
9. [2024·福州一中月考]在△ABC中,内角A,B,C所对的边分别为a,b,c,且2bcosA = 2c - a.
(1)求角B;
(2)若a = 4,b = 2√7,求边BC上的中线AD的长.
(1)求角B;
(2)若a = 4,b = 2√7,求边BC上的中线AD的长.
答案:
9.
(1)因为$2b\cos A=2c-a$,所以$2b×\frac{b^{2}+c^{2}-a^{2}}{2bc}=2c-a$,即$a^{2}+c^{2}-b^{2}=ac$,由余弦定理的推论可得$\cos B=\frac{c^{2}+a^{2}-b^{2}}{2ca}=\frac{1}{2}$.因为$0<B<\pi$,所以$B=\frac{\pi}{3}$.
(2)由$b^{2}=c^{2}+c^{2}-2c\cos B$,得$28=c^{2}+16-4c$,解得$c=6$或$c=-2$(舍去).
在$\triangle ABD$中,$AB=6,BD=\frac{1}{2}BC=2,\angle ABD=\frac{\pi}{3}$,则$AD^{2}=AB^{2}+BD^{2}-2× AB· BD\cos\angle ABD=36+4-2×6×2×\frac{1}{2}=28$,故$AD=2\sqrt{7}$.
(1)因为$2b\cos A=2c-a$,所以$2b×\frac{b^{2}+c^{2}-a^{2}}{2bc}=2c-a$,即$a^{2}+c^{2}-b^{2}=ac$,由余弦定理的推论可得$\cos B=\frac{c^{2}+a^{2}-b^{2}}{2ca}=\frac{1}{2}$.因为$0<B<\pi$,所以$B=\frac{\pi}{3}$.
(2)由$b^{2}=c^{2}+c^{2}-2c\cos B$,得$28=c^{2}+16-4c$,解得$c=6$或$c=-2$(舍去).
在$\triangle ABD$中,$AB=6,BD=\frac{1}{2}BC=2,\angle ABD=\frac{\pi}{3}$,则$AD^{2}=AB^{2}+BD^{2}-2× AB· BD\cos\angle ABD=36+4-2×6×2×\frac{1}{2}=28$,故$AD=2\sqrt{7}$.
查看更多完整答案,请扫码查看


