2025年热搜题高中数学必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年热搜题高中数学必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第114页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. [2024·吉安一中月考]已知一组数据 $ x_{1},x_{2},x_{3},x_{4},x_{5} $ 的平均数是 $ \overline{x}=2 $,方差是 $ \frac{1}{3} $,那么另一组数据 $ 3x_{1}-2,3x_{2}-2,3x_{3}-2,3x_{4}-2,3x_{5}-2 $ 的平均数和方差分别为(
A.$ 2,\frac{1}{3} $
B.$ 2,1 $
C.$ 4,\frac{1}{3} $
D.$ 4,3 $
D
)A.$ 2,\frac{1}{3} $
B.$ 2,1 $
C.$ 4,\frac{1}{3} $
D.$ 4,3 $
答案:
1.D 【解析】平均数为$\bar{x}'=3x - 2=3×2 - 2=4$,方差为$s'^{2}=9s^{2}=9×\frac{1}{3}=3$。
2. [2024·杭州二中月考]设样本数据 $ x_{1},x_{2},·s,x_{2024} $ 的平均数为 $ \overline{x} $,方差为 $ s^{2} $,若数据 $ 2(x_{1}+1),2(x_{2}+1),·s,2(x_{2024}+1) $ 的平均数比方差大4,则 $ s^{2}-\overline{x}^{2} $ 的最大值为(
A.$ -1 $
B.$ \frac{1}{2} $
C.$ -2 $
D.$ 1 $
A
)A.$ -1 $
B.$ \frac{1}{2} $
C.$ -2 $
D.$ 1 $
答案:
2.A 【解析】设数据$2(x_{1}+1),2(x_{2}+1),·s,2(x_{2024}+1)$的平均数为$\bar{x}_{0}$,方差为$s_{0}^{2}$,则$\bar{x}_{0}=2(\bar{x}+1),s_{0}^{2}=4s^{2}$,由题意可得$2(\bar{x}+1)=4s^{2}+4$,所以$s^{2}=\frac{1}{2}\bar{x}-\frac{1}{2}$,则$s^{2}-\bar{x}^{2}=\frac{1}{2}\bar{x}-\frac{1}{2}-\bar{x}^{2}=-(\bar{x}-\frac{1}{4})^{2}-\frac{7}{16}$。因为$s^{2}=\frac{1}{2}\bar{x}-\frac{1}{2}\geqslant0$,所以$\bar{x}\geqslant1$,故当$\bar{x}=1$时,$s^{2}-\bar{x}^{2}$取得最大值$-1$。故选A。
3. [2024·商丘一中期末]一名射击运动员连续射击5次,所得环数的平均数为8,标准差为1.2,则这5次射击不可能出现的环数是(
A.5
B.6
C.7
D.8
A
)A.5
B.6
C.7
D.8
答案:
3.A 【解析】由标准差为$1.2$,得方差为$1.44$。设$5$次射击的环数分别为$x_{1},x_{2},x_{3},x_{4},x_{5}$,则$\frac{1}{5}\sum_{i = 1}^{5}(x_{i}-8)^{2}=1.44$,所以若出现$5$环,则$\frac{(5 - 8)^{2}}{5}=1.8>1.44$,故不可能出现$5$环;若出现$6$环、$7$环、$8$环,均可以使得$\frac{1}{5}\sum_{i = 1}^{5}(x_{i}-8)^{2}=1.44$有解,故可以出现。故选A。
4. [2024·陕西师大附中期中](多选)甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则(
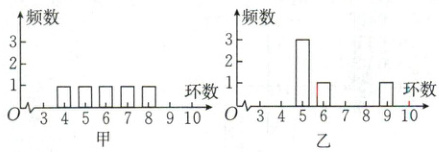
A.甲的成绩的平均数小于乙的成绩的平均数
B.甲的成绩的中位数等于乙的成绩的中位数
C.甲的成绩的方差小于乙的成绩的方差
D.甲的成绩的极差等于乙的成绩的极差
CD
)
A.甲的成绩的平均数小于乙的成绩的平均数
B.甲的成绩的中位数等于乙的成绩的中位数
C.甲的成绩的方差小于乙的成绩的方差
D.甲的成绩的极差等于乙的成绩的极差
答案:
4.CD 【解析】由题意可知,甲的成绩为$4,5,6,7,8$,乙的成绩为$5,5,5,6,9$,所以甲、乙的成绩的平均数均为$6$,A错误;甲、乙的成绩的中位数分别为$6,5$,B错误;甲、乙的成绩的方差分别为$\frac{1}{5}×[(4 - 6)^{2}+(5 - 6)^{2}+(6 - 6)^{2}+(7 - 6)^{2}+(8 - 6)^{2}]=2$,$\frac{1}{5}×[(5 - 6)^{2}+(5 - 6)^{2}+(5 - 6)^{2}+(6 - 6)^{2}+(9 - 6)^{2}]=\frac{12}{5}$,C正确;甲、乙的成绩的极差均为$4$,D正确。故选CD。
5. [2024·株洲三中月考]已知样本9,10,11,$ x $,$ y $ 的平均数是10,标准差为 $ \sqrt{2} $,则 $ xy= $
96
.
答案:
5.96 【解析】由平均数得$9 + 10 + 11 + x + y = 50$,所以$x + y = 20$。由标准差得$(9 - 10)^{2}+(10 - 10)^{2}+(11 - 10)^{2}+(x - 10)^{2}+(y - 10)^{2}=(\sqrt{2})^{2}×5 = 10$,所以$x^{2}+y^{2}-20(x + y)= - 192$,故$(x + y)^{2}-2xy - 20(x + y)= - 192$,所以$xy = 96$。
6. [2024·威海一中期末]若40个数据的平方和是56,平均数是 $ \frac{\sqrt{2}}{2} $,则这组数据的方差是
0.9
,标准差是$\frac{3\sqrt{10}}{10}$
.
答案:
6.$0.9\frac{3\sqrt{10}}{10}$ 【解析】设这$40$个数据为$x_{i}(i = 1,2,·s,40)$,平均数为$\bar{x}$。
则$s^{2}=\frac{1}{40}[(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+·s+(x_{40}-\bar{x})^{2}]$
$=\frac{1}{40}[x_{1}^{2}+x_{2}^{2}+·s+x_{40}^{2}+40\bar{x}^{2}-2\bar{x}(x_{1}+x_{2}+·s+x_{40})]$
$=\frac{1}{40}×[56 + 40×(\frac{\sqrt{2}}{2})^{2}-2×\frac{\sqrt{2}}{2}×40×\frac{\sqrt{2}}{2}]$
$=\frac{1}{40}×(56 - 40×\frac{1}{2})=0.9$
所以$s=\sqrt{0.9}=\sqrt{\frac{9}{10}}=\frac{3\sqrt{10}}{10}$。
则$s^{2}=\frac{1}{40}[(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+·s+(x_{40}-\bar{x})^{2}]$
$=\frac{1}{40}[x_{1}^{2}+x_{2}^{2}+·s+x_{40}^{2}+40\bar{x}^{2}-2\bar{x}(x_{1}+x_{2}+·s+x_{40})]$
$=\frac{1}{40}×[56 + 40×(\frac{\sqrt{2}}{2})^{2}-2×\frac{\sqrt{2}}{2}×40×\frac{\sqrt{2}}{2}]$
$=\frac{1}{40}×(56 - 40×\frac{1}{2})=0.9$
所以$s=\sqrt{0.9}=\sqrt{\frac{9}{10}}=\frac{3\sqrt{10}}{10}$。
7. [2024·乐山一中月考](多选)某高中有学生500人,其中男生有300人,女生有200人,希望获得全体学生的身高(单位:cm)信息,按照分层随机抽样的方法抽取了容量为50的样本,经计算得到男生身高的样本均值为170,方差为17;女生身高样本均值为160,方差为30.下列说法中正确的有(
A.样本中男生的人数为30
B.每个女生入样的概率均为 $ \frac{2}{5} $
C.所有样本的均值为166
D.所有样本的方差为22.2
AC
)A.样本中男生的人数为30
B.每个女生入样的概率均为 $ \frac{2}{5} $
C.所有样本的均值为166
D.所有样本的方差为22.2
答案:
7.AC 【解析】对于A,由题意,得样本中男生有$\frac{50}{500}×300 = 30$(人),故A正确。对于B,每个女生入样的概率为$\frac{50}{500}=\frac{1}{10}$,故B不正确。对于C,由分层随机抽样知,样本中男生有$30$人,女生有$20$人,所有样本的均值为$\frac{170×30 + 160×20}{50}=166$,故C正确。对于D,设样本中男生的身高分别为$x_{1},x_{2},·s,x_{30}$,平均数$\bar{x}=170,s_{x}^{2}=17$,样本中女生的身高分别为$y_{1},y_{2},·s,y_{20}$,平均数$\bar{y}=160,s_{y}^{2}=30$,总体的平均数为$\bar{z}=166$,方差为$s^{2}$,则$s^{2}=\frac{1}{50}[\sum_{i = 1}^{30}(x_{i}-166)^{2}+\sum_{i = 1}^{20}(y_{i}-166)^{2}]$。因为$\sum_{i = 1}^{30}(x_{i}-166)^{2}=\sum_{i = 1}^{30}[(x_{i}-170)+(170 - 166)]^{2}=\sum_{i = 1}^{30}(x_{i}-170)^{2}+2\sum_{i = 1}^{30}(x_{i}-170)(170 - 166)$,而$\sum_{i = 1}^{30}(x_{i}-170)(170 - 166)=4×(\sum_{i = 1}^{30}x_{i}-30×170)=0$,所以$\sum_{i = 1}^{30}(x_{i}-166)^{2}=\sum_{i = 1}^{30}(x_{i}-170)^{2}+\sum_{i = 1}^{30}(170 - 166)^{2}=30×17 + 4^{2}×30 = 990$,同理可得$\sum_{i = 1}^{20}(y_{i}-166)^{2}=\sum_{i = 1}^{20}(y_{i}-160)^{2}+\sum_{i = 1}^{20}(160 - 166)^{2}=20×30+6^{2}×20 = 1320$,所以$s^{2}=\frac{1}{50}×(990 + 1320)=46.2$,故D不正确。故选AC。
8. [2024·郑州一中月考]在了解全校学生每年平均阅读了多少本文学经典名著时,甲同学抽取了一个容量为10的样本,并算得样本的平均数为5,方差为9;乙同学抽取了一个容量为8的样本,并算得样本的平均数为6,方差为16.已知甲、乙两同学抽取的样本合在一起组成一个容量为18的样本,求合在一起后的样本平均数与方差.(精确到0.1)
答案:
8.把甲同学抽取的样本的平均数记为$\bar{x}$,方差为$s_{x}^{2}$;把乙同学抽取的样本的平均数记为$\bar{y}$,方差记为$s_{y}^{2}$;把合在一起的样本的平均数记为$\bar{a}$,方差记为$s^{2}$。则$\bar{a}=\frac{10×5 + 8×6}{10 + 8}\approx5.4$,
$s^{2}=\frac{10×[s_{x}^{2}+(\bar{x}-\bar{a})^{2}]+8×[s_{y}^{2}+(\bar{y}-\bar{a})^{2}]}{10 + 8}$
$=\frac{10×[9+(5 - 5.4)^{2}]+8×[16+(6 - 5.4)^{2}]}{18}$
$\approx12.4$
即样本的平均数为$5.4$,方差为$12.4$。
$s^{2}=\frac{10×[s_{x}^{2}+(\bar{x}-\bar{a})^{2}]+8×[s_{y}^{2}+(\bar{y}-\bar{a})^{2}]}{10 + 8}$
$=\frac{10×[9+(5 - 5.4)^{2}]+8×[16+(6 - 5.4)^{2}]}{18}$
$\approx12.4$
即样本的平均数为$5.4$,方差为$12.4$。
查看更多完整答案,请扫码查看


