第97页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
12. [易错题]在$\triangle ABC$中,$\angle ABC = 90°$,$AC = 5$,$BC = 4$,以$AC为边作\triangle ACD$,使得$\angle ACD = 90°$。如果$\triangle ABC与\triangle ACD$相似,那么$CD$的长为
$\frac{15}{4}$或$\frac{20}{3}$
。
答案:
$\frac{15}{4}$或$\frac{20}{3}$
13. [2025·舞钢期末]如图,$\triangle ABC,\triangle GCD,\triangle FDE$是三个全等的等腰三角形,点$B,C,D,E$在一条直线上,且$AB = \sqrt{3}$,$BC = 1$,$BF交AC于点P$。
(1)求证:$\triangle BFE\sim\triangle FDE$;
(2)求$CP$的长。

(1)求证:$\triangle BFE\sim\triangle FDE$;
(2)求$CP$的长。

答案:
(1)提示:利用两边成比例且夹角相等的两个三角形相似进行证明.
(2)解:$CP=\frac{\sqrt{3}}{3}$.
(1)提示:利用两边成比例且夹角相等的两个三角形相似进行证明.
(2)解:$CP=\frac{\sqrt{3}}{3}$.
14. 新考向 跨物理·小孔成像 [2024·扬州中考]物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图像投影的方法。如图,燃烧的蜡烛(竖直放置)$AB经小孔O$在屏幕(竖直放置)上成像$A'B'$。若$AB = 36cm$,$A'B' = 24cm$,小孔$O到AB的距离为30cm$,则小孔$O到A'B'$的距离为

20
$cm$。
答案:
20
15. 新考向 情境题·容器截面图 [2025·郑州郑东新区期末]如图①是装了液体的长方体容器的截面图,将容器按图②所示方式倾斜后,水面恰好接触到容器口的边缘,则此时水面宽度$AB$为(
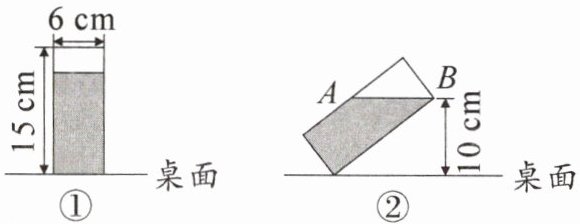
A.$9cm$
B.$10cm$
C.$11cm$
D.$12cm$
A
)
A.$9cm$
B.$10cm$
C.$11cm$
D.$12cm$
答案:
A
16. 如图,小明用灯泡$O照射一个矩形硬纸片ABCD$,在墙上形成矩形影子$A'B'C'D'$。现测得$OA = 10cm$,$OA' = 25cm$,纸片$ABCD的面积为16cm^2$,则影子$A'B'C'D'$的面积为
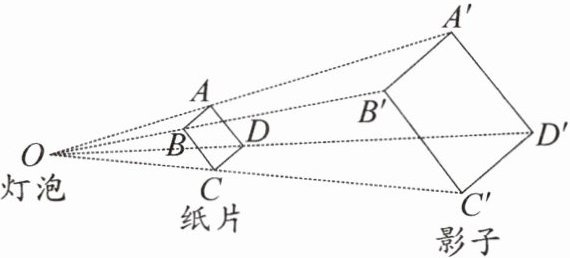
100
$cm^2$。
答案:
100
17. 如图,在平面直角坐标系中,已知$\triangle A_1B_1C_1与\triangle ABC$位似,$\triangle ABC的顶点坐标分别是A(2,1)$,$B(3,4)$,$C(2,3)$,$\triangle A_1B_1C_1的顶点坐标分别是A_1(-4,4)$,$B_1(-6,-2)$,$C_1(-4,0)$。
(1)若位似中心为点$M$,请写出点$M$的坐标:
(2)以点$O$为位似中心,作$\triangle A_1B_1C_1的位似图形\triangle A_2B_2C_2$,使$\triangle A_1B_1C_1与\triangle A_2B_2C_2的相似比为2:1$,请在图中画出符合要求的$\triangle A_2B_2C_2$,并写出点$B_2$的坐标。
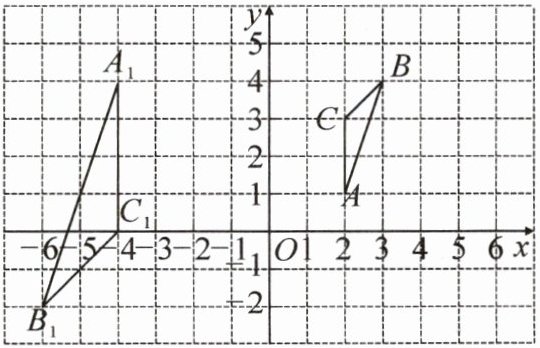
(1)若位似中心为点$M$,请写出点$M$的坐标:
(0,2)
;(2)以点$O$为位似中心,作$\triangle A_1B_1C_1的位似图形\triangle A_2B_2C_2$,使$\triangle A_1B_1C_1与\triangle A_2B_2C_2的相似比为2:1$,请在图中画出符合要求的$\triangle A_2B_2C_2$,并写出点$B_2$的坐标。

图略,点$B_{2}$的坐标为(3,1)或(-3,-1).
答案:
(1)(0,2)
(2)图略,点$B_{2}$的坐标为(3,1)或(-3,-1).
(1)(0,2)
(2)图略,点$B_{2}$的坐标为(3,1)或(-3,-1).
查看更多完整答案,请扫码查看


