《2025年状元成才路创优作业九年级数学上册北师大版》

1. [2024·山西中考]一个不透明的盒子里装有一个红球、一个白球和一个绿球,这些球除颜色外其他都相同.从中随机摸出一个球,记下颜色后不放回,再从中随机摸出一个球,则两次摸到的球中恰好有一个红球的概率是(B)
A.$\frac{1}{3}$
B.$\frac{2}{3}$
C.$\frac{4}{9}$
D.$\frac{5}{9}$

答案： B

2. [2024·安阳汤阴县期末]在$a^{2}□4a□4的空格□$中,任意填上“+”号或“-”号,在所有得到的代数式中,能构成完全平方式的概率是(B)
A.1
B.$\frac{1}{2}$
C.$\frac{1}{3}$
D.$\frac{1}{4}$

答案： B

3. 某校运动会$4×400m$的接力赛中,甲、乙两名同学都是各自小组的第一棒,这两名同学各自从四个赛道中随机抽取一个赛道,则他们恰好抽中相邻赛道的概率为(A)
A.$\frac{1}{2}$
B.$\frac{1}{4}$
C.$\frac{1}{6}$
D.$\frac{1}{8}$

答案： A

4. 新考向 数学文化 圆周率$π$是无限不循环小数.历史上,祖冲之、刘徽、韦达、欧拉等数学家都对$π$有过深入的研究.某校进行校园文化建设,拟从以上4位数学家的画像中随机选用2幅,则其中至少有一幅是中国数学家的概率是$\frac{5}{6}$.

答案： $\frac{5}{6}$

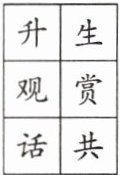
5. 新考向 跨语文·古诗 小唐参加学校组织的“诗词大会”,需要从图中的6个字中选出正确的两个字,填入诗句“海上______明月,天涯______此时”.如果他不知道答案从而任意选择,那么他答对的概率为$\frac{1}{30}$.

答案： $\frac{1}{30}$

6. 端午节早上,小颖为全家人蒸了2个蛋黄粽,3个蜜枣粽,她从中随机挑选了两个孝敬爷爷奶奶,则爷爷奶奶吃到同类粽子的概率是$\frac{2}{5}$.

答案： $\frac{2}{5}$

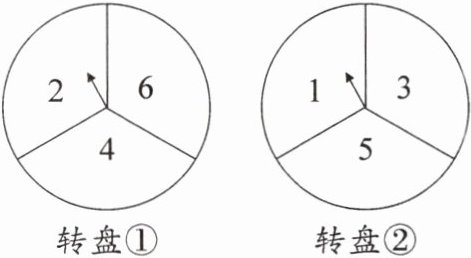
7. 如图,有两个可以自由转动的转盘,被等分成了三个扇形区域,每个区域分别标有数字.小杰先转动转盘①,停止后记下指针指向的数字；小玉再转动转盘②,停止后记下指针指向的数字.若指针指在分界线上,则重转.
(1)请用列表或画树状图的方法表示出所有可能出现的结果.
(2)若得到的两数之和是3的倍数,则小杰赢；若得到的两数之和是7的倍数,则小玉赢；若得到的两数之和既不是3的倍数也不是7的倍数,则平局.此游戏公平吗？为什么？

答案：
7.解:
(1)列表如下:

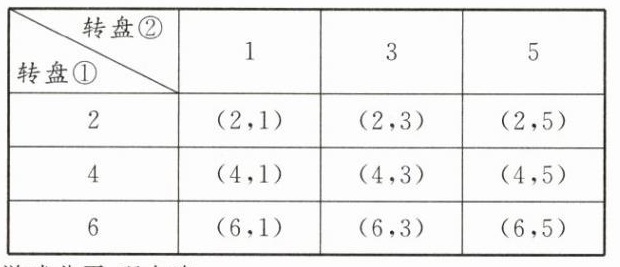
(2)此游戏公平.理由略.

8. 有4张正面分别写有数字$-2$,$-1$,0,1的卡片,它们的背面完全相同,现将这4张卡片背面朝上洗匀.
(1)从中任意抽取一张卡片,则所抽卡片上数字的绝对值不大于1的概率是多少？
(2)先从中任意抽取一张卡片,以其正面数字作为$m$的值,然后再从剩余的卡片中随机抽取一张,以其正面数字作为$n$的值,请用列表法或画树状图法求点$A(m,n)$在第三象限的概率.

答案： 8.解:
(1)所抽卡片上数字的绝对值不大于1的概率是$\frac{3}{4}$.
(2)点$A(m,n)$在第三象限的概率为$\frac{1}{6}$.