第26页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
综合与实践 在矩形纸片上折出含 $ 30^{\circ} $ 的角
在数学活动课上,老师让同学们以“在矩形纸片上折出含 $ 30^{\circ} $ 的角”为主题开展数学活动.
【操作与证明】
小张的操作步骤如下:
第一步:如图①,折出正方形 $ ABEF $ 后,沿 $ EF $ 翻折,得到正方形 $ EFMN $,再把纸片展平;
第二步:如图②,过点 $ M $ 沿 $ GM $ 翻折,使点 $ A $ 落在 $ BC $ 上,对应点为 $ A' $.
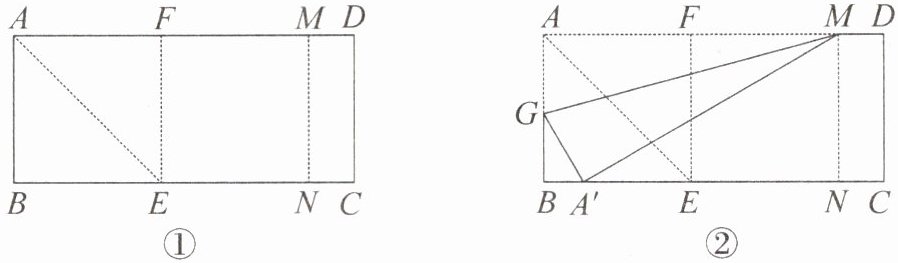
(1)①求证:$ \angle MA'N = 30^{\circ} $;
②若 $ AB = 2 $,求 $ AG $ 的长.
【迁移与应用】
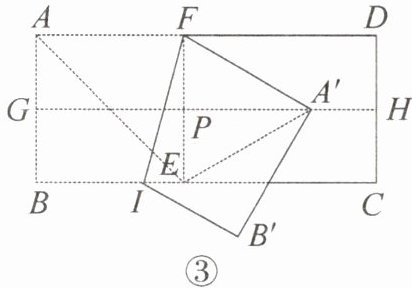
(2)小李说,在小张折出正方形 $ ABEF $ 后,将矩形纸片上下对折,再把纸片展开,折痕为 $ GH $,$ GH $ 与 $ EF $ 交于点 $ P $,过点 $ F $ 沿 $ IF $ 折叠四边形 $ ABIF $,使点 $ A $ 的对应点 $ A' $ 落在 $ GH $ 上,连接 $ A'E $,如图③,这样也可得到 $ 30^{\circ} $ 的角.请你直接写出一个 $ 30^{\circ} $ 的角.
在数学活动课上,老师让同学们以“在矩形纸片上折出含 $ 30^{\circ} $ 的角”为主题开展数学活动.
【操作与证明】
小张的操作步骤如下:
第一步:如图①,折出正方形 $ ABEF $ 后,沿 $ EF $ 翻折,得到正方形 $ EFMN $,再把纸片展平;
第二步:如图②,过点 $ M $ 沿 $ GM $ 翻折,使点 $ A $ 落在 $ BC $ 上,对应点为 $ A' $.

(1)①求证:$ \angle MA'N = 30^{\circ} $;
②若 $ AB = 2 $,求 $ AG $ 的长.
【迁移与应用】
(2)小李说,在小张折出正方形 $ ABEF $ 后,将矩形纸片上下对折,再把纸片展开,折痕为 $ GH $,$ GH $ 与 $ EF $ 交于点 $ P $,过点 $ F $ 沿 $ IF $ 折叠四边形 $ ABIF $,使点 $ A $ 的对应点 $ A' $ 落在 $ GH $ 上,连接 $ A'E $,如图③,这样也可得到 $ 30^{\circ} $ 的角.请你直接写出一个 $ 30^{\circ} $ 的角.

答案:
(1)①证明:如图②,取A′M的中点P,连接PN.

由题意,得∠A′NM=90°,MN=AB= $\frac{1}{2}$AM= $\frac{1}{2}$A′M.
∴PM=PN=A′P= $\frac{1}{2}$A′M.
∴PN=MN=PM.
∴△PMN为等边三角形.
∴∠PMN=60°.
在Rt△A′MN中,∠MA′N=180°-∠A′NM-∠A′MN=180°-90°-60°=30°.
②解:
∵AB=2,
∴AM=A′M=2AB=2×2=4,MN=2,
∴在Rt△A′MN中,A′N= $\sqrt{A'M^2-MN^2}$ = $\sqrt{4^2-2^2}$ =2 $\sqrt{3}$.
由题意,得BN=AM=4,
∴A′B=BN-A′N=4-2 $\sqrt{3}$.
设AG=x,则A′G=x,BG=AB-AG=2-x.
在Rt△A′BG中,根据勾股定理,得BG²+A′B²=A′G²,
即(2-x)²+(4-2 $\sqrt{3}$)²=x²,解得x=8-4 $\sqrt{3}$.
∴AG的长为8-4 $\sqrt{3}$.
(2)解:∠EA′B′=30°.(答案不唯一,∠FA′P=∠EA′P=∠A′FD =∠A′EC=∠B′IC=30°)
(1)①证明:如图②,取A′M的中点P,连接PN.

由题意,得∠A′NM=90°,MN=AB= $\frac{1}{2}$AM= $\frac{1}{2}$A′M.
∴PM=PN=A′P= $\frac{1}{2}$A′M.
∴PN=MN=PM.
∴△PMN为等边三角形.
∴∠PMN=60°.
在Rt△A′MN中,∠MA′N=180°-∠A′NM-∠A′MN=180°-90°-60°=30°.
②解:
∵AB=2,
∴AM=A′M=2AB=2×2=4,MN=2,
∴在Rt△A′MN中,A′N= $\sqrt{A'M^2-MN^2}$ = $\sqrt{4^2-2^2}$ =2 $\sqrt{3}$.
由题意,得BN=AM=4,
∴A′B=BN-A′N=4-2 $\sqrt{3}$.
设AG=x,则A′G=x,BG=AB-AG=2-x.
在Rt△A′BG中,根据勾股定理,得BG²+A′B²=A′G²,
即(2-x)²+(4-2 $\sqrt{3}$)²=x²,解得x=8-4 $\sqrt{3}$.
∴AG的长为8-4 $\sqrt{3}$.
(2)解:∠EA′B′=30°.(答案不唯一,∠FA′P=∠EA′P=∠A′FD =∠A′EC=∠B′IC=30°)
查看更多完整答案,请扫码查看


