第77页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
9. 已知△ABC 的三边长分别为 4,6,8,△A′B′C′其中一边的长为 2,若要使△ABC∽△A′B′C′,则△A′B′C′其他两边的长分别为
3,4 或$\frac{4}{3},\frac{8}{3}$或$1,\frac{3}{2}$
。
答案:
3,4 或$\frac{4}{3},\frac{8}{3}$或$1,\frac{3}{2}$
10. 新考向 传统文化·中国象棋 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,要使“马”“车”“炮”所在位置的格点构成的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似,则“马”应落在
(
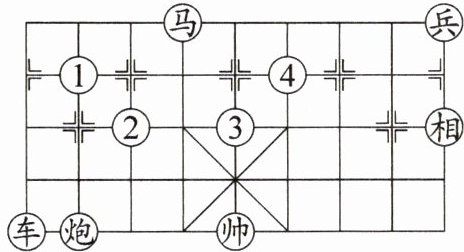
A.①处
B.②处
C.③处
D.④处
(
B
)
A.①处
B.②处
C.③处
D.④处
答案:
B
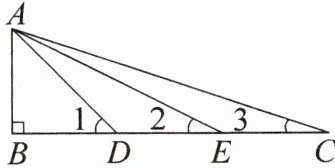
11. 如图,在△ABC 中,∠B = 90°,点 D,E 在 BC 上,且 AB = BD = DE = EC。求证:
(1)△ADE∽△CDA;
(2)∠1 + ∠2 + ∠3 = 90°。
]
(1)△ADE∽△CDA;
(2)∠1 + ∠2 + ∠3 = 90°。
]

答案:
(1)提示:证明$\frac{AD}{CD}=\frac{DE}{DA}=\frac{AE}{CA}$.
(2)证明:$\because \triangle ADE \backsim \triangle CDA$,$\therefore \angle EAD=\angle 3$.$\because \angle B=90^{\circ}$,$AB=BD$,$\therefore \angle 1=45^{\circ}$.又$\because \angle 1=\angle 2+\angle EAD$,$\therefore \angle 2+\angle 3=45^{\circ}$.$\therefore \angle 1+\angle 2+\angle 3=45^{\circ}+45^{\circ}=90^{\circ}$.
(1)提示:证明$\frac{AD}{CD}=\frac{DE}{DA}=\frac{AE}{CA}$.
(2)证明:$\because \triangle ADE \backsim \triangle CDA$,$\therefore \angle EAD=\angle 3$.$\because \angle B=90^{\circ}$,$AB=BD$,$\therefore \angle 1=45^{\circ}$.又$\because \angle 1=\angle 2+\angle EAD$,$\therefore \angle 2+\angle 3=45^{\circ}$.$\therefore \angle 1+\angle 2+\angle 3=45^{\circ}+45^{\circ}=90^{\circ}$.
12. 新考向 类比探究 学习“探索三角形相似的条件”后,我们可以借助探索两个直角三角形全等的条件所获得的经验,继续探索两个直角三角形相似的条件。
(1)“对于两个直角三角形,满足一边一锐角对应相等或两直角边对应相等,两个直角三角形全等”。类似地,可以得到“对于两个直角三角形,满足
(2)“满足斜边和一条直角边对应相等的两个直角三角形全等”。类似地,可以得到“满足
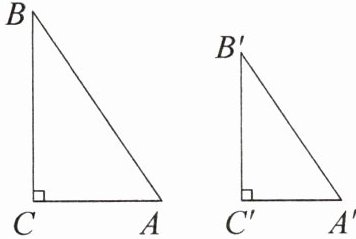
(3)对于(2),请结合下列所给图形,写出已知,并完成证明过程。
已知:如图,
求证:Rt△ABC∽Rt△A′B′C′。
]
(1)“对于两个直角三角形,满足一边一锐角对应相等或两直角边对应相等,两个直角三角形全等”。类似地,可以得到“对于两个直角三角形,满足
一个锐角对应相等
或两直角边对应成比例
,两个直角三角形相似”。(2)“满足斜边和一条直角边对应相等的两个直角三角形全等”。类似地,可以得到“满足
斜边和一条直角边对应成比例
的两个直角三角形相似”。(3)对于(2),请结合下列所给图形,写出已知,并完成证明过程。
已知:如图,
在$Rt\triangle ABC$和$Rt\triangle A'B'C'$中,$AB$,$A'B'$为斜边,且$\frac{AB}{A'B'}=\frac{AC}{A'C'}$
。求证:Rt△ABC∽Rt△A′B′C′。
]

证明:设$\frac{AB}{A'B'}=\frac{AC}{A'C'}=k(k>0)$,则$AB=kA'B'$,$AC=kA'C'$.在$Rt\triangle ABC$和$Rt\triangle A'B'C'$中,$\frac{BC}{B'C'}=\frac{\sqrt{AB^{2}-AC^{2}}}{\sqrt{A'B'^{2}-A'C'^{2}}}=\sqrt{\frac{k^{2}A'B'^{2}-k^{2}A'C'^{2}}{A'B'^{2}-A'C'^{2}}}=k$,$\therefore \frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}$,$\therefore Rt\triangle ABC \backsim Rt\triangle A'B'C'$.
答案:
解:
(1)一个锐角对应相等 两直角边对应成比例
(2)斜边和一条直角边对应成比例
(3)在$Rt\triangle ABC$和$Rt\triangle A'B'C'$中,$AB$,$A'B'$为斜边,且$\frac{AB}{A'B'}=\frac{AC}{A'C'}$证明:设$\frac{AB}{A'B'}=\frac{AC}{A'C'}=k(k>0)$,则$AB=kA'B'$,$AC=kA'C'$.在$Rt\triangle ABC$和$Rt\triangle A'B'C'$中,$\frac{BC}{B'C'}=\frac{\sqrt{AB^{2}-AC^{2}}}{\sqrt{A'B'^{2}-A'C'^{2}}}=\sqrt{\frac{k^{2}A'B'^{2}-k^{2}A'C'^{2}}{A'B'^{2}-A'C'^{2}}}=k$,$\therefore \frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}$,$\therefore Rt\triangle ABC \backsim Rt\triangle A'B'C'$.
(1)一个锐角对应相等 两直角边对应成比例
(2)斜边和一条直角边对应成比例
(3)在$Rt\triangle ABC$和$Rt\triangle A'B'C'$中,$AB$,$A'B'$为斜边,且$\frac{AB}{A'B'}=\frac{AC}{A'C'}$证明:设$\frac{AB}{A'B'}=\frac{AC}{A'C'}=k(k>0)$,则$AB=kA'B'$,$AC=kA'C'$.在$Rt\triangle ABC$和$Rt\triangle A'B'C'$中,$\frac{BC}{B'C'}=\frac{\sqrt{AB^{2}-AC^{2}}}{\sqrt{A'B'^{2}-A'C'^{2}}}=\sqrt{\frac{k^{2}A'B'^{2}-k^{2}A'C'^{2}}{A'B'^{2}-A'C'^{2}}}=k$,$\therefore \frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}$,$\therefore Rt\triangle ABC \backsim Rt\triangle A'B'C'$.
查看更多完整答案,请扫码查看


