第28页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 菱形具有而平行四边形不一定具有的性质是(
A.对角线互相平分
B.对角线互相垂直
C.对边平行
D.有一个角是 $90^{\circ}$
B
)A.对角线互相平分
B.对角线互相垂直
C.对边平行
D.有一个角是 $90^{\circ}$
答案:
B
2. 如图,$□ ABCD$ 的对角线 $AC$,$BD$ 相交于点 $O$,添加以下条件仍不能判定 $□ ABCD$ 是菱形的是(
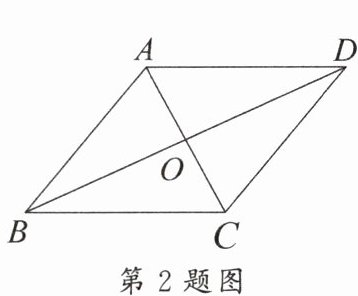
A.$\angle BAC= \angle BCA$
B.$\angle ABD= \angle CBD$
C.$OA^{2}+OB^{2}= AD^{2}$
D.$AD^{2}+OA^{2}= OD^{2}$
]
D
)
A.$\angle BAC= \angle BCA$
B.$\angle ABD= \angle CBD$
C.$OA^{2}+OB^{2}= AD^{2}$
D.$AD^{2}+OA^{2}= OD^{2}$
]
答案:
D
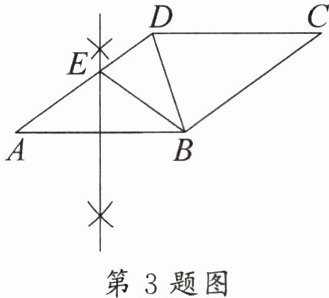
3. 新考向 尺规作图 如图,在菱形 $ABCD$ 中,$\angle A = 36^{\circ}$,分别以点 $A$,$B$ 为圆心,以大于 $\frac{1}{2}AB$ 的长为半径画弧交于两点,过此两点的直线交 $AD$ 边于点 $E$,连接 $BE$,$BD$,则 $\angle EBD$ 的度数为
]
36°
。]

答案:
36°
4. 如图,在 $\triangle ABC$ 中,$\angle BCA = 90^{\circ}$,$CD$ 是边 $AB$ 上的中线,分别过点 $C$,$D$ 作 $AB$ 和 $BC$ 的平行线,两线交于点 $E$,且 $DE$ 交 $AC$ 于点 $O$,连接 $AE$。
(1)求证:四边形 $ADCE$ 是菱形;
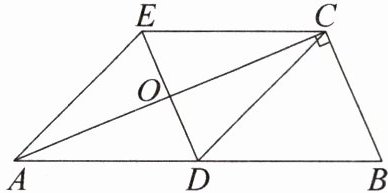
(2)若 $\angle B = 60^{\circ}$,$BC = 6$,则四边形 $ADCE$ 的面积为
]
(1)求证:四边形 $ADCE$ 是菱形;

(2)若 $\angle B = 60^{\circ}$,$BC = 6$,则四边形 $ADCE$ 的面积为
18√3
。]
答案:
(1)提示:利用有一组邻边相等的平行四边形是菱形进行证明.
(2)18√3
(1)提示:利用有一组邻边相等的平行四边形是菱形进行证明.
(2)18√3
5. 新考向 情境题·矩形鼠标垫 如图,诚诚用橡胶皮和布料自制了一块四边形鼠标垫,为了检验这块鼠标垫是不是标准的矩形,他想出了以下几种方案,其中合理的是(

A.测量一组对边是否平行且相等
B.测量两组对边是否分别相等
C.测量其中的三个角是否都为直角
D.测量对角线是否相等
]
C
)
A.测量一组对边是否平行且相等
B.测量两组对边是否分别相等
C.测量其中的三个角是否都为直角
D.测量对角线是否相等
]
答案:
C
6. [2025·舞钢期末]如图,在矩形 $ABCD$ 中,对角线 $AC$ 与 $BD$ 相交于点 $O$,$AE$ 垂直平分 $OB$,$E$ 是垂足。若 $AB = \sqrt{3}$,则 $AD$ 的长是(
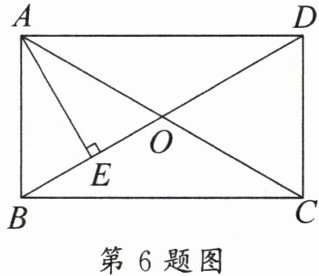
A.$2$
B.$3$
C.$2\sqrt{3}$
D.$\sqrt{5}$
]
B
)
A.$2$
B.$3$
C.$2\sqrt{3}$
D.$\sqrt{5}$
]
答案:
B
7. 新考向 传统文化·翻花绳 翻花绳是中国民间流传的儿童游戏。如图①是翻花绳的一种图案,可以抽象成图②,在矩形 $ABCD$ 中,$IJ// KL$,$EF// GH$,$\angle 1 = \angle 2 = 30^{\circ}$,则 $\angle 3$ 的度数为
]
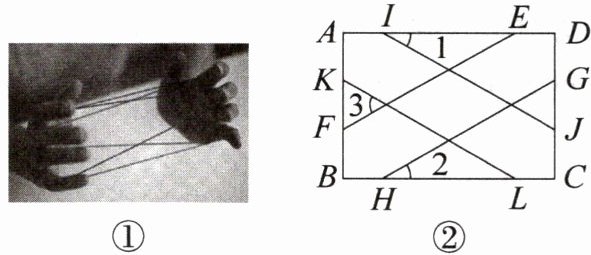
60°
。]

答案:
60°
8. [易错题]在矩形 $ABCD$ 中,$M$ 为对角线 $BD$ 的中点,点 $N$ 在边 $AD$ 上,且 $AN = AB = 1$。当以点 $D$,$M$,$N$ 为顶点的三角形是直角三角形时,$AD$ 的长为
2或1+√2
。
答案:
2或1+√2
查看更多完整答案,请扫码查看


