《2025年状元成才路创优作业九年级数学上册北师大版》

1. 下列各数中,是方程 $2x^{2}+5x = 3$ 的根的是(A)
A.$-3$
B.$-1$
C.$1$
D.$3$

答案： A

2. [2024·郑州管城区期末]若 $x = 4$ 是关于 $x$ 的方程 $x^{2}+bx - 6 = 0$ 的解,则 $b$ 的值为-5/2。
变式题组 [条件变式]
(1)已知 $m$ 是一元二次方程 $x^{2}+x - 6 = 0$ 的一个根,则代数式 $m^{2}+m$ 的值为6；
(2)若 $x = 2$ 是关于 $x$ 的一元二次方程 $x^{2}+mx + 2n = 0$ 的一个根,则 $m + n= $-2。

答案： -5/2 [变式题组]
(1)6
(2)-2

3. 新考向 开放性问题[2025·洛阳期末]写出一个一元二次方程,使它有一个根为 $1$,则这个方程可以为x²-1=0(答案不唯一)。

答案： x²-1=0(答案不唯一)

4. 下列表格是 $x$ 与 $ax^{2}+bx + c$ 的五组对应值,若 $x_{1}$ 是方程 $ax^{2}+bx + c = 0$ 的一个解,且 $x_{1}＞1.6$,则下列选项中正确的是(C)

A.$1.6＜x_{1}＜1.8$
B.$1.8＜x_{1}＜2.0$
C.$2.0＜x_{1}＜2.2$
D.$2.2＜x_{1}＜2.4$

答案： C

5. 在确定一元二次方程 $x^{2}+2x - 4 = 0$ 的近似解时,小明所在的小组采用了赋值法,计算结果如表：

小组同学说,他们发现了该方程的一个近似解。这个近似解的十分位上的数字是2。

答案： 2

6. [易错题]已知关于 $x$ 的一元二次方程 $(a - 1)x^{2}-2x + a^{2}-1 = 0$ 有一个根为 $x = 0$,则 $a$ 的值为(C)
A.$0$
B.$\pm1$
C.$-1$
D.$1$

答案： C

7. 如果关于 $x$ 的一元二次方程 $ax^{2}+bx + c = 0(a\neq0)$ 满足 $a + b + c = 0$,那么该方程一定有一个根为(B)
A.$0$
B.$1$
C.$-1$
D.$2$

答案： B

8. [整体思想][2024·南充中考]已知 $m$ 是方程 $x^{2}+4x - 1 = 0$ 的一个根,则 $(m + 5)(m - 1)$ 的值为-4。

答案： -4

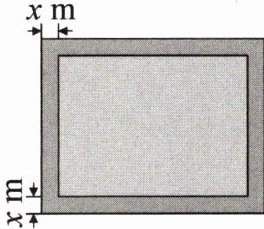
9. 如图,某大学为改善校园环境,计划在一块长 $80m$、宽 $60m$ 的矩形场地中央建一个矩形操场,操场占地面积为 $3500m^{2}$,四周为宽度相等的人行通道,设人行通道的宽为 $x m$。
(1)请列出相应的方程。
(2)$x$ 的值可能小于 $0$ 吗？可能大于 $30$ 吗？请说明理由。
(3)求人行通道的宽。

答案： 解:
(1)依题意,得(80-2x)(60-2x)=3500.整理,得x²-70x+325=0.
(2)x的值不可能小于0,也不可能大于30.理由略.
(3)人行通道的宽为5m.