《2025年状元成才路创优作业九年级数学上册北师大版》

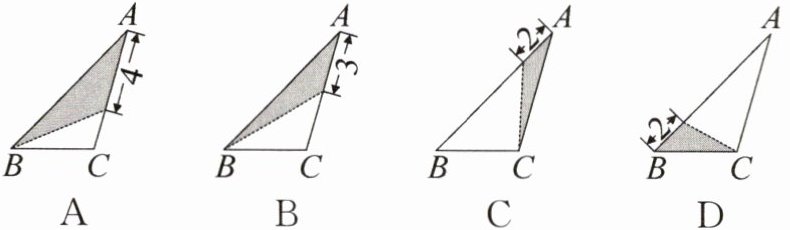
9. 新考向 动手操作 [2025·汝州期中]在三角形纸片$ABC$中,$AB = 8$,$BC = 4$,$AC = 6$,按下列方法沿虚线裁剪,能使阴影部分的三角形与$\triangle ABC$相似的是 (D)

答案： D

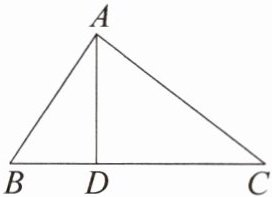
10. 如图,在$\triangle ABC$中,$D为BC$上一点,$BC = \sqrt{3}AB = 3BD$,则$AD:AC$的值为$\frac{\sqrt{3}}{3}$。

答案： $\frac{\sqrt{3}}{3}$

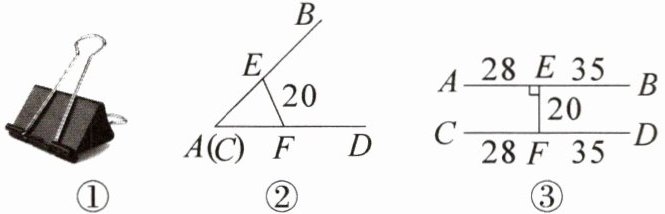
11. 新考向 情境题·燕尾夹 一种燕尾夹如图①所示,图②是其在闭合状态时的示意图,图③是其在某打开状态时的示意图(数据单位：$mm$),此时$AB // CD$,则从图②闭合状态到图③打开状态,点$B$,$D$之间的距离减少了25$mm$。

答案： 25

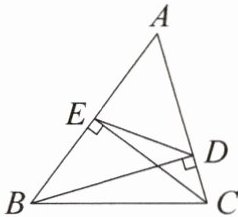
12. 如图,在$\triangle ABC$中,$BD \perp AC$,$CE \perp AB$,垂足分别是$D$,$E$,连接$DE$。
(1)求证：$\triangle ACE \backsim \triangle ABD$；
(2)若$BD = 8$,$AD = 6$,$DE = 5$,求$BC$的长。

答案：
(1)提示:利用两角分别相等的两个三角形相似进行证明.
(2)解:$BC=\frac{25}{3}$.

13. 如图,已知$\angle MON = 90°$,$A是\angle MON$内一点,$AB \perp ON于点B$,$AB = 3cm$,$OB = 4cm$,动点$E$,$F同时从点O$出发,点$E以1.5cm/s的速度沿ON$方向运动,点$F以2cm/s的速度沿OM$方向运动,$EF与OA相交于点C$。当点$E到达点B$处时,点$E$,$F$同时停止运动,设运动时间为$t\ s(t ＞ 0)$。
(1)当$t = 1$时,$\triangle EOF与\triangle ABO$是否相似？请说明理由。
(2)在运动过程中,无论$t$取何值,总有$EF \perp OA$,为什么？

答案：
(1)△EOF∽△ABO.理由略.
(2)在运动过程中,OE=1.5t cm,OF=2t cm.
∵AB=3 cm,OB=4 cm, $\therefore \frac{OE}{AB}=\frac{t}{2},\frac{OF}{OB}=\frac{t}{2}\therefore \frac{OE}{BA}=\frac{OF}{BO}$. 又
∵∠EOF=∠ABO=90°,
∴△EOF∽△ABO.
∴∠EFO=∠AOB.
∵∠AOB+∠FOC=90°,
∴∠EFO+∠FOC=90°.
∴∠FCO=90°,即EF⊥OA.
∴无论t取何值,总有EF⊥OA.