《2025年状元成才路创优作业九年级数学上册北师大版》

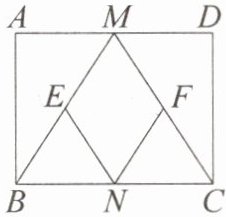
5. 如图,在矩形 $ABCD$ 中,$M$,$N$ 分别是边 $AD$,$BC$ 的中点,$E$,$F$ 分别是线段 $BM$,$CM$ 的中点。
(1) 求证：$\triangle ABM\cong\triangle DCM$；
(2) 当 $AB:AD$ 的值为多少时,四边形 $MENF$ 是正方形？请说明理由。

答案：
(1)提示:利用“SAS”进行证明.
(2)解:当AB:AD=1:2时，四边形MENF是正方形.理由略.

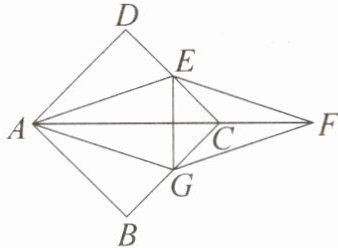
6. 新考向 情境题·制作风筝 如图是小明自制的风筝框架示意图,在正方形框架 $ABCD$ 和平行四边形框架 $AEFG$ 中,$E$,$G$ 恰好分别是 $CD$,$BC$ 的中点,连接 $EG$,点 $A$,$C$,$F$ 在同一条直线上。
(1) 求证：四边形 $AEFG$ 为菱形；
(2) 若 $AB = 40\mathrm{cm}$,求风筝的长度($AF$ 的长)。

答案：
(1)提示:利用有一组邻边相等的平行四边形是菱形进行证明.
(2)解:风筝的长度为60√2 cm.

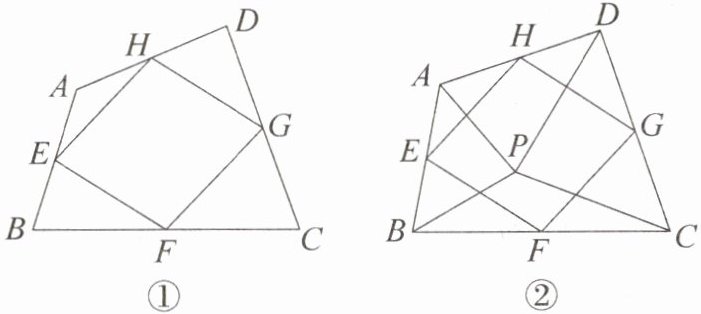
7. 新考向 类比探究 我们给出如下定义：顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形。

(1) 平行四边形如图①,在四边形 $ABCD$ 中,点 $E$,$F$,$G$,$H$ 分别为边 $AB$,$BC$,$CD$,$DA$ 的中点,则中点四边形 $EFGH$ 是____；
(2) 如图②,$P$ 是四边形 $ABCD$ 内一点,且满足 $PA = PB$,$PC = PD$,$\angle APB = \angle CPD$,点 $E$,$F$,$G$,$H$ 分别为边 $AB$,$BC$,$CD$,$DA$ 的中点。猜想中点四边形 $EFGH$ 的形状,并证明你的猜想；
(3) 中点四边形EFGH是正方形.若改变 (2) 中的条件,使 $\angle APB = \angle CPD = 90^{\circ}$,其他条件不变,直接写出中点四边形 $EFGH$ 的形状(不必证明)。

答案：
(1)平行四边形
(2)中点四边形EFGH是菱形.证明如下:如图②，连接AC,BD交于点O.
∵∠APB=∠CPD,
∴∠APB + ∠APD = ∠CPD + ∠APD,即∠BPD=∠APC.在△APC和△BPD中,
∵PA=PB,∠APC=∠BPD,PC=PD,
∴△APC≌△BPD(SAS),
∴AC=BD.
∵点E,F,G分别为边AB,BC,CD的中点,
∴EF=1/2AC,FG=1/2BD,
∴EF=FG.由
(1)知中点四边形EFGH是平行四边形,
∴□EFGH是菱形.
(3)中点四边形EFGH是正方形.