第84页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
7. 如图,△ABC是测量小玻璃管内径的量具,AB的长为18mm,AC被分为60等份。如果小玻璃管口DE正好对着量具上20等份处(点D,E分别在AC,BC上,且DE//AB),那么小玻璃管内径DE的长为(
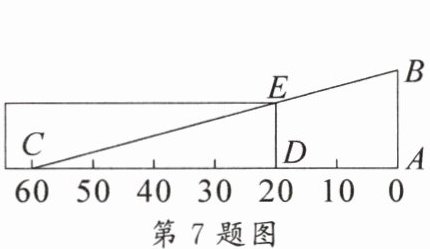
A.8mm
B.10mm
C.12mm
D.15mm
C
)
A.8mm
B.10mm
C.12mm
D.15mm
答案:
C
8. 如图,社会实践小组的同学们想利用树影测量树高。课外活动时他们在阳光下测得一根长为1m的竹竿的影长是0.9m,同一时刻测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的台阶上,且影子的末端刚好落在最后一级台阶的上端C处。他们测得落在地面的影长为1.1m,台阶总高度为1.0m,台阶水平总宽度为1.6m,则树高为

4
m。
答案:
4
9. [2025·南阳内乡县期中]如图,某校社会实践小组为了测量一次大型运动会的主火炬台顶端距离地面的高度,小明先在地面上C处竖直设立了高度为2m的标杆CD,这时地面上的点E、标杆的顶端D、火炬台的顶端B正好在同一直线上,测得CE= 3m;小明再从点E出发沿着EG方向前进9m到达点F,并在点F处放置一平面镜,小刚站在点G处时,恰好在平面镜中看到火炬台顶端B的像,此时测得小刚的眼睛到地面的距离HG为1.5m,GF= 3m。已知点G,F,E,C与火炬台的底端A在同一直线上,AB⊥AG,CD⊥AG,HG⊥AG。(平面镜的大小忽略不计)
(1)求AE与AB的数量关系;
(2)请你根据以上数据,计算该火炬台的高度AB。
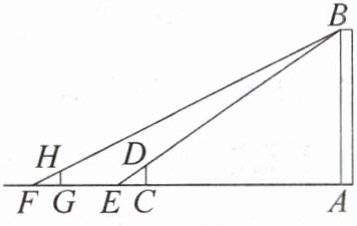
(1)求AE与AB的数量关系;
(2)请你根据以上数据,计算该火炬台的高度AB。

答案:
解:
(1)AE 与 AB 的数量关系为 $ AE=\frac{3}{2}AB $.
(2)该火炬台的高度 AB 为 18 m.
(1)AE 与 AB 的数量关系为 $ AE=\frac{3}{2}AB $.
(2)该火炬台的高度 AB 为 18 m.
10. 如图,为了测量一栋楼的高度OE,小明同学先在操场A处放一面镜子,向后退到B处,恰好在镜子中看到楼的顶部E;再将镜子放到C处,然后后退到D处,恰好再次在镜子中看到楼的顶部E(点O,A,B,C,D在同一条直线上),测得AC= 2m,BD= 2.1m。若小明的眼睛离地面的高度BF= DG= 1.6m,试确定楼的高度OE。(注:反射角= 入射角)


答案:
解:由题意,得$ \angle OAE=\angle BAF $,$ \angle OCE=\angle DCG $.$ \because \angle AOE=\angle ABF=90° $,$ \angle COE=\angle CDG=90° $,$ \therefore \triangle AOE \backsim \triangle ABF $,$ \triangle COE \backsim \triangle CDG $,$ \therefore \frac{OE}{BF}=\frac{AO}{AB} $,$ \frac{OE}{DG}=\frac{CO}{CD} $.$ \because BF=DG=1.6\ m $,$ \therefore \frac{AO}{AB}=\frac{CO}{CD}=\frac{OE}{1.6} $,$ \therefore \frac{CO-AO}{CD-AB}=\frac{OE}{1.6} $,即$ \frac{AC}{BD-AC}=\frac{OE}{1.6} $.$ \because AC=2\ m $,$ BD=2.1\ m $,$ \therefore \frac{2}{2.1-2}=\frac{OE}{1.6} $,$ \therefore OE=32\ m $.答:楼的高度 OE 为 32 m.
查看更多完整答案,请扫码查看


