第6页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. [2025·佛山禅城区期中]已知菱形 $ABCD$ 的对角线 $BD = 12$,$AC = 10$,则该菱形的面积为(
A.60
B.80
C.100
D.120
A
)A.60
B.80
C.100
D.120
答案:
A
2. 如图,在菱形 $ABCD$ 中,$AB = 10$,$\angle D = 45^{\circ}$,则菱形的面积为
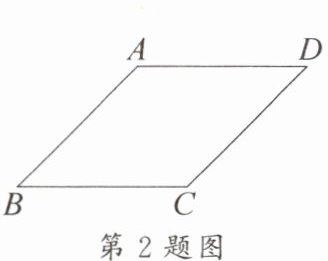
50√2
。
答案:
50√2
3. 如图,四边形 $ABCD$ 是菱形,$AC$ 与 $BD$ 相交于点 $O$,$OA = 4$,$OD = 3$,$DH \perp AB$ 于点 $H$,则 $DH = $
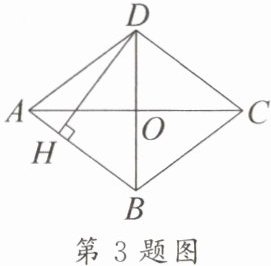
4.8
。
答案:
4.8
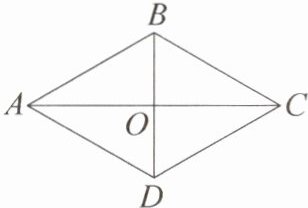
4. 如图,菱形 $ABCD$ 的对角线 $AC$ 与 $BD$ 相交于点 $O$,$\angle BAD = 60^{\circ}$,菱形 $ABCD$ 的边长为 6。求:
(1)对角线 $BD$ 的长;
(2)菱形 $ABCD$ 的面积。
(1)对角线 $BD$ 的长;
(2)菱形 $ABCD$ 的面积。

答案:
解:
(1)BD=6.
(2)菱形 ABCD 的面积为18√3.
(1)BD=6.
(2)菱形 ABCD 的面积为18√3.
5. 如图,在 $□ ABCD$ 中,$\angle 1 = \angle 2$,$AB = 3$,则四边形 $ABCD$ 的周长为(
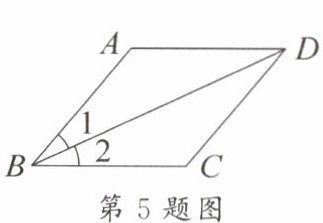
A.15
B.12
C.9
D.6
B
)
A.15
B.12
C.9
D.6
答案:
B
6. 如图,在 $□ ABCD$ 中,$AC \perp BD$,$\angle ABD = 40^{\circ}$,则 $\angle ADC$ 的度数为(
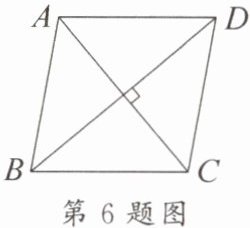
A.$70^{\circ}$
B.$75^{\circ}$
C.$80^{\circ}$
D.$85^{\circ}$
C
)
A.$70^{\circ}$
B.$75^{\circ}$
C.$80^{\circ}$
D.$85^{\circ}$
答案:
C
7. 新考向 尺规作图 如图,在 $\angle MON$ 的两边分别截取 $OA$,$OB$,使 $OA = OB$;分别以点 $A$,$B$ 为圆心,以 $OA$ 的长为半径作弧,两弧交于点 $C$,连接 $AC$,$BC$,$AB$,$OC$,则下列结论不一定成立的是(
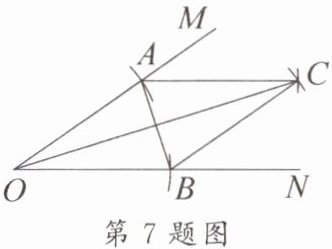
A.$OA = BC$
B.$AB \perp OC$
C.$AC // OB$
D.$AB = AC$
D
)
A.$OA = BC$
B.$AB \perp OC$
C.$AC // OB$
D.$AB = AC$
答案:
D
8. [教材 P8“做一做”变式题]如图,两张等宽且对边平行的纸条交叉重叠在一起,重叠的部分为四边形 $ABCD$。若测得点 $A$,$C$ 之间的距离为 $6\mathrm{cm}$,点 $B$,$D$ 之间的距离为 $8\mathrm{cm}$,则线段 $AB$ 的长为
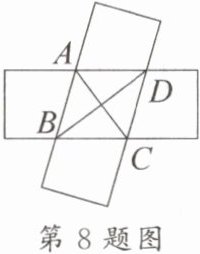
5
$\mathrm{cm}$。
答案:
5
9. 新考向 情境题·吊灯 [2025·遵义期末节选]小颖家新房买了一盏简单而精致的吊灯(如图①),其正面的示意图大致如图②所示。四边形 $ABCD$ 是一个菱形外框架,对角线 $AC$,$BD$ 相交于点 $O$,四边形 $AECF$ 是其内部框架,点 $E$,$F$ 在 $BD$ 上,且 $BE = DF$。求证:四边形 $AECF$ 是菱形。
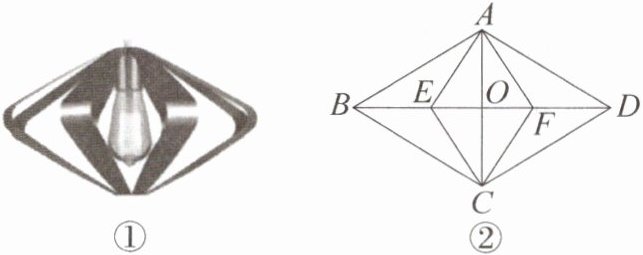

答案:
提示:利用对角线互相垂直的平行四边形是菱形进行证明.
查看更多完整答案,请扫码查看


