《2025年状元成才路创优作业九年级数学上册北师大版》

1. 如图,B是线段AC的黄金分割点($AB＞BC$),则下列结论中,正确的是(C)

A.$AC^{2}= AB^{2}+BC^{2}$
B.$BC^{2}= AC\cdot AB$
C.$\frac {AB}{AC}= \frac {BC}{AB}$
D.$\frac {BC}{AC}= \frac {\sqrt {5}-1}{2}$

答案： C

2. [2024·山西中考]黄金分割是汉字结构最基本的规律.借助如图的正方形习字格书写的汉字“晋”端庄稳重、舒展美观.已知一条分割线的端点A,B分别在习字格的边MN,PQ上,且$AB// NP$,“晋”字的笔画“、”的位置在AB的黄金分割点C处,且$\frac {BC}{AB}= \frac {\sqrt {5}-1}{2}$.若$NP= 2cm$,则BC的长为$(\sqrt{5}-1)$cm.(结果保留根号)

答案： $(\sqrt{5}-1)$

3. 新考向 传统文化·二胡 二胡是中国古老的民族拉弦乐器之一.音乐家发现,二胡的千斤线绑在琴弦的黄金分割点处时,奏出来的音调最和谐、最悦耳.如图,一把二胡的琴弦AC长为80 cm,千斤线绑在靠近上端点A的琴弦的黄金分割点B处,则点B上方的琴弦AB的长为$(120-40\sqrt{5})$cm.(结果保留根号)

答案： $(120-40\sqrt{5})$

4. 已知线段AB的长度为2,点C是线段AB的黄金分割点,则AC的长度为$\sqrt{5}-1$或$3-\sqrt{5}$.

答案： $\sqrt{5}-1$或$3-\sqrt{5}$

5. [教材P97随堂练习变式题]摄影中有一种拍摄手法叫黄金构图法,其原理是：如图,在正方形ABCD的边BC上取中点E,以点E为圆心,线段DE的长为半径作弧,与边BC的延长线交于点F,矩形ABFG称为黄金矩形(宽与长的比等于$\frac {\sqrt {5}-1}{2}$的矩形叫做黄金矩形).若$CF= 4$,则AB的长为$2\sqrt{5}+2$.

答案： $2\sqrt{5}+2$

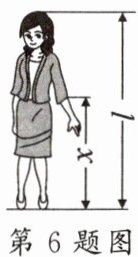
6. 美是一种感觉,人体下半身长与身高的比值越接近0.618,就越能够给人一种美感.如图,某女士身高165 cm,下半身长x与身高l的比值是0.60,为尽可能达到好的效果,她穿的高跟鞋的高度应大约为8cm.(结果取整数)

答案： 8

7. 新考向 阅读理解·新定义型 类似于“黄金分割点”,给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分,这两部分的面积分别为$S_{1},S_{2}$,如果$\frac {S_{1}}{S}= \frac {S_{2}}{S_{1}}$,那么称直线l为该图形的“黄金分割线”.如图,在$\triangle ABC$中,$∠A= 36^{\circ },AB= AC,∠ACB$的平分线交AB于点D.求证：
(1)$\triangle CBD\backsim \triangle ABC$；
(2)直线CD是$\triangle ABC$的“黄金分割线”.

答案：
(1)利用两角分别相等的两个三角形相似进行证明.
(2)证明$\frac{S_{\triangle ADC}}{S_{\triangle ABC}}=\frac{S_{\triangle CBD}}{S_{\triangle ADC}}$.