《2025年状元成才路创优作业九年级数学上册北师大版》

6. [2024·武汉中考]经过某十字路口的汽车,可能直行,也可能向左转或向右转,这三种可能性大小相同.若两辆汽车经过这个十字路口,则至少有一辆车向右转的概率是(D)
A.$\frac{1}{9}$
B.$\frac{1}{3}$
C.$\frac{4}{9}$
D.$\frac{5}{9}$

答案： D

7. 斗兽棋是我国一种古老的棋类游戏,双方各有八枚棋子,从大到小的顺序为象、狮、虎、豹、狼、狗、猫、鼠,除鼠胜象外,较大的战胜较小的.在一次对局中,莉莉手中存有的棋子为虎、猫,牛牛手中存有的棋子为狮、豹,双方将手中棋子的背面向上,随机从自己的棋子中抽取一个进行比较,则莉莉获胜的概率为(A)

A.$\frac{1}{4}$
B.$\frac{1}{2}$
C.$\frac{3}{4}$
D.0

答案： A

8. 小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么小李获胜的概率为(A)

A.$\frac{13}{25}$
B.$\frac{12}{25}$
C.$\frac{4}{25}$
D.$\frac{1}{2}$

答案： A

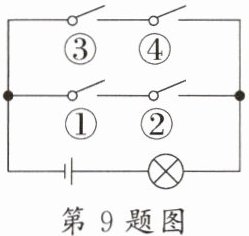
9. 新考向 跨物理·电路图 如图,电路上有编号①②③④的 4 个开关和 1 个小灯泡,任意闭合电路上的两个开关,小灯泡发光的概率为$\frac{1}{3}$.

答案： $\frac{1}{3}$

10. [2024·新郑期末]已知四边形 $ABCD$ 的对角线为 $AC$,$BD$,有下列四个条件：①$AD // BC$,$AB // CD$；②$AD // BC$,$AD = BC$；③$AC = BD$；④$AC \perp BD$.
(1)从中任选一个作为条件,能判定四边形 $ABCD$ 是平行四边形的概率是$\frac{1}{2}$；
(2)从中任选两个作为条件,请用画树状图或列表的方法计算能判定四边形 $ABCD$ 是矩形的概率(每个条件在列表或画图时用前边对应的序号表示).
解:(2)任选两个作为条件,能判定四边形ABCD是矩形的概率为$\frac{1}{3}$.

答案： 解:
(1)$\frac{1}{2}$
(2)任选两个作为条件,能判定四边形ABCD是矩形的概率为$\frac{1}{3}$.

11. 有甲、乙两个不透明的口袋,甲口袋中装有两个球,它们分别写有数 $-2$,$2$；乙口袋中装有三个球,它们分别写有数 $-5$,$m$,$5$,这些小球除数字外其他完全相同.小明和小刚进行摸球游戏,规则如下：先从甲口袋中随机取出一个球,其上的数记为 $a$；再从乙口袋中随机取出一个球,其上的数记为 $b$.若 $a ＜ b$,则小明获胜；若 $a = b$,则为平局；若 $a ＞ b$,则小刚获胜.
(1)若 $m = -2$,用画树状图或列表的方法分别求出小明、小刚获胜的概率；
(2)当 $m$ 为何值时,小明和小刚获胜的概率相同？直接写出一个符合条件的整数 $m$ 的值.

答案： 解:
(1)小明获胜的概率为$\frac{1}{3}$,小刚获胜的概率为$\frac{1}{2}$.
(2)$m=0$或$-1$或1,任选其一.