《2025年状元成才路创优作业九年级数学上册北师大版》

7. 设 $m$ 是方程 $x^{2}+5x = 0$ 的一个较大的根,$n$ 是方程 $x^{2}-3x + 2 = 0$ 的一个较小的根,则 $m + n$ 的值是(C)
A.$-4$
B.$-3$
C.$1$
D.$2$

答案： C

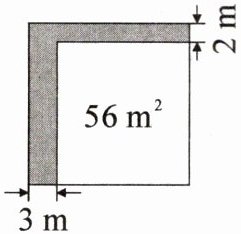
8. [教材 P48 习题 T3 变式题]如图,从一块正方形空地上划出部分区域栽种鲜花(阴影部分),原空地一边减少了 $3m$,另一边减少了 $2m$,剩余空地面积为 $56m^{2}$,则原正方形空地的边长为10m.

答案： 10

9. 三角形两边的长分别是 $2$ 和 $3$,第三边的长是方程 $x^{2}-10x + 24 = 0$ 的根,则该三角形的周长为9.

答案： 9

10. 用因式分解法解下列方程：
(1) $(2 - 3x)+(3x - 2)^{2}= 0$；
(2) $x^{2}-9 = 7(x + 3)$；
(3) $(x - 2)^{2}= (5 - 2x)^{2}$.

答案： 解$:(1)x₁=1,x₂=\frac{2}{3}.(2)x₁=-3,x₂=10.(3)x₁=3,x₂=\frac{7}{3}.$

11. [新定义问题]定义：若两个一元二次方程有且只有一个相同的实数根,我们就称这两个方程为“同伴方程”. 例如 $x^{2}= 4$ 和 $(x - 2)(x + 3)= 0$ 有且只有一个相同的实数根 $x = 2$,所以这两个方程为“同伴方程”. 若关于 $x$ 的一元二次方程 $x^{2}-2x = 0$ 与 $x^{2}+3x + m - 1 = 0$ 为“同伴方程”,则 $m$ 的值为1 或-9.

答案： 1 或-9

阅读下列材料：
将 $ x^{2}+2x - 35 $ 因式分解,我们可以按下面的方法解答：
① 分解二次项与常数项：
$ x^{2}= x\cdot x $,$ -35 = (-5)×(+7) $.
② 交叉相乘,验中项：
$\Rightarrow 7x - 5x = 2x$.
③ 横向写出两因式：
$ x^{2}+2x - 35= (x - 5)(x + 7) $.
我们将这种用十字交叉相乘因式分解的方法称为十字相乘法.
试用上述方法解下列方程：
(1)$ x^{2}+6x + 8 = 0 $； (2)$ x^{2}-7x + 6 = 0 $；
(3)$ x^{2}+3x - 10 = 0 $； (4)$ 2x^{2}-5x - 3 = 0 $.

答案：
(1)$x_{1}=-2$,$x_{2}=-4$.
(2)$x_{1}=1$,$x_{2}=6$.
(3)$x_{1}=-5$,$x_{2}=2$.
(4)$x_{1}=3$,$x_{2}=-\frac{1}{2}$.