第47页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
7. 将一块矩形桌布铺在长为 3 m、宽为 2 m 的矩形桌面上,各边下垂的长度相同,并且桌布的面积是桌面面积的 2 倍,那么桌布下垂的长度为 (
A.1.5 m
B.2.5 m
C.0.5 m
D.1 m
C
)A.1.5 m
B.2.5 m
C.0.5 m
D.1 m
答案:
C
8. 如图,有一张长 32 cm、宽 16 cm 的矩形硬纸片,裁去角上 2 个小正方形和 2 个小矩形(图中阴影部分)之后,恰好折成一个有盖纸盒.若纸盒的底面积是 $130cm^2$,则纸盒的高为

3
cm。
答案:
3
9. 如图,一架长为 15 m 的梯子 $AB$ 斜靠在墙上,梯子的顶端 $A$ 离地面的距离为 12 m.
(1) 如果梯子的顶端从 $A$ 处沿墙下滑了 1 m,那么梯子的底端也从 $B$ 处向右滑动 1 m 吗?
(2) 梯子的顶端从 $A$ 处沿墙下滑的距离与梯子的底端从 $B$ 处向右滑动的距离有可能相等吗?若有可能,请求出这个距离;若没有可能,请说明理由.
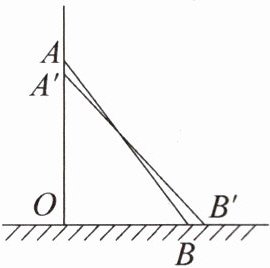
(1) 如果梯子的顶端从 $A$ 处沿墙下滑了 1 m,那么梯子的底端也从 $B$ 处向右滑动 1 m 吗?
(2) 梯子的顶端从 $A$ 处沿墙下滑的距离与梯子的底端从 $B$ 处向右滑动的距离有可能相等吗?若有可能,请求出这个距离;若没有可能,请说明理由.

答案:
(1)梯子的底端不是从B处向右滑动1 m.
(2)有可能相等.这个距离是3 m.
(1)梯子的底端不是从B处向右滑动1 m.
(2)有可能相等.这个距离是3 m.
10. 如图,在矩形 $ABCD$ 中,$AB = 5cm$,$BC = 6cm$,点 $P$ 从点 $A$ 开始沿边 $AB$ 向点 $B$ 以 1 cm/s 的速度运动,点 $Q$ 从点 $B$ 开始沿边 $BC$ 向点 $C$ 以 2 cm/s 的速度运动.如果点 $P$,$Q$ 同时出发,当点 $Q$ 运动到点 $C$ 处时,两点都停止运动.设运动时间为 $t$ s($t>0$).
(1) 当 $t$ 为何值时,$PQ$ 的长度等于 5 cm?
(2) 是否存在 $t$ 的值,使得五边形 $APQCD$ 的面积等于 $26cm^2$?若存在,请求出此时 $t$ 的值;若不存在,请说明理由.
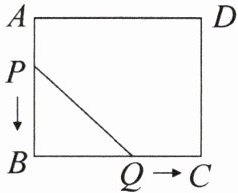
(1) 当 $t$ 为何值时,$PQ$ 的长度等于 5 cm?
(2) 是否存在 $t$ 的值,使得五边形 $APQCD$ 的面积等于 $26cm^2$?若存在,请求出此时 $t$ 的值;若不存在,请说明理由.

答案:
(1)依题意,得BQ=2t cm,PB=(5-t)cm. 在Rt△PBQ中,由勾股定理,得PB²+BQ²=PQ², 即(5-t)²+(2t)²=5²,解得t₁=0(不合题意,舍去),t₂=2. 故当t=2时,PQ的长度等于5 cm.
(2)存在.矩形ABCD的面积是6×5=30(cm²). 要使得五边形APQCD的面积等于26 cm²,则△PBQ的面积为30-26=4(cm²).所以$\frac{1}{2}×2t×(5-t)=4$,解得t₁=4,t₂=1. 当t=4时,BQ=2t=8>6,故t=4不合题意,舍去. 所以此时t的值为1.
(1)依题意,得BQ=2t cm,PB=(5-t)cm. 在Rt△PBQ中,由勾股定理,得PB²+BQ²=PQ², 即(5-t)²+(2t)²=5²,解得t₁=0(不合题意,舍去),t₂=2. 故当t=2时,PQ的长度等于5 cm.
(2)存在.矩形ABCD的面积是6×5=30(cm²). 要使得五边形APQCD的面积等于26 cm²,则△PBQ的面积为30-26=4(cm²).所以$\frac{1}{2}×2t×(5-t)=4$,解得t₁=4,t₂=1. 当t=4时,BQ=2t=8>6,故t=4不合题意,舍去. 所以此时t的值为1.
查看更多完整答案,请扫码查看


