《2025年综合应用创新题典中点六年级数学上册鲁教版五四制》

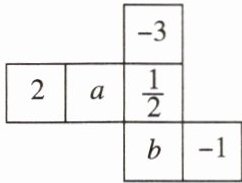
11. [新趋势学科内综合]如图是正方体纸盒的表面展开图,纸面上写有数字和字母,其中$a$与其对面的数互为相反数,$b$与其对面的数互为倒数。
(1)填空：$a = $1,$b = $______$-\frac{1}{3}$；
(2)先化简,再求值：$-3(ab - a^{2})-[2b^{2}-(5ab - a^{2})+2ab]$。

答案： [解]
(1)1；$-\frac{1}{3}$
(2) - 3(ab - a²)-[2b² - (5ab - a²)+2ab]= - 3ab + 3a² - (2b² - 5ab + a²+2ab)= - 3ab + 3a² - 2b²+5ab - a² - 2ab=( - 3ab + 5ab - 2ab)+(3a² - a²)-2b² = 2a² - 2b².因为a = 1,b = $-\frac{1}{3}$,所以原式=2×1² - 2×$(-\frac{1}{3})^{2}$ = 2 - $\frac{2}{9}$ = $\frac{16}{9}$.

12. [新情境生活应用]某电商平台需要定制一种上盖为双层的长方体外包装纸箱(如图①),上盖纸板面积等于底面面积的2倍,并且每个外包装纸箱刚好能装入两个同样大小的小包装盒(如图②),设装入时不留空隙,且纸箱厚度忽略不计。已知每个小包装盒的长、宽、高分别为$a$,$b$,$c$,且$a = c$,$b ＜ a$。现有如图②所示的甲、乙两种放入纸箱的摆放方式。

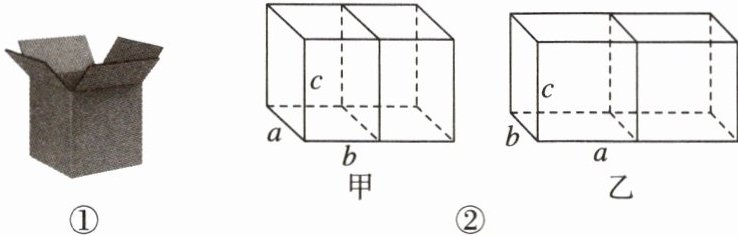
(1)分别计算甲、乙两种摆放方式所需外包装纸箱的纸板面积；(用含$a$,$b$的代数式表示)
(2)当$a = 20 cm$,$b = 12 cm$时,问电商平台选择哪种摆放方式,所需纸箱的纸板面积较少？

答案： [解]
(1)因为a = c,所以甲种摆放方式所需外包装纸箱的纸板面积为2ac + 2×2bc + 3×2ab = 2ac + 4bc + 6ab = 2a²+10ab,乙种摆放方式所需外包装纸箱的纸板面积为2×2ac + 2bc + 3×2ab = 4ac + 2bc + 6ab = 4a²+8ab.
(2)当a = 20cm,b = 12cm时,甲种摆放方式所需纸板面积为2×20²+10×20×12 = 3200(cm²),乙种摆放方式所需纸板面积为4×20²+8×20×12 = 3520(cm²).因为3200＜3520，所以甲种摆放方式所需纸箱的纸板面积较少.

13. [2025·常德期末][新视角·新定义题]给定有理数$a$,$b$,对整式$A$,$B$,定义新运算“$\oplus$”：$A\oplus B = aA + bB$；对正整数$n(n\geq2)和整式A$,定义新运算“$\otimes$”：$n\otimes A= \underbrace{A\oplus A…\oplus\oplus A}_{n个A}$(按从左到右的顺序依次做“$\oplus$”运算)。特别地,$1\otimes A = A$。例如,当$a = 1$,$b = 2$时,若$A = x$,$B = -y$,则$A\oplus B = A + 2B = x - 2y$,$2\otimes A = A\oplus A = 3x$。
(1)当$a = 2$,$b = 1$时,若$A = x + y$,$B = x - 2y$,则
①$A\oplus B = $3x,$2\otimes A = $3x + 3y；
②$n\otimes A = $$(2^{n}-1)(x + y)$；
(2)当$a = 2$,$b = 1$时,若$A = 2x^{2}-y$,$B = x^{2}+18y$,$P = n\otimes A$,$Q = 3\otimes B$,且$P\oplus Q的值与y$的取值无关,求整数$n$的值。
由(1)②知$P = n\otimes A=(2^{n}-1)A$,$Q = 3\otimes B=(2^{3}-1)B = 7B$.因为$A = 2x² - y$,$B = x²+18y$,所以$P\oplus Q = 2P + Q = 2(2^{n}-1)A + 7B =(2^{n + 1}-2)A + 7B =(2^{n + 1}-2)(2x² - y)+7(x²+18y)=(2^{n + 2}+3)x²+(128 - 2^{n + 1})y$.因为$P\oplus Q$的值与$y$的取值无关，所以$128 - 2^{n + 1}=0$,所以$n = 6$.

答案： [解]
(1)①3x；3x + 3y ②$(2^{n}-1)(x + y)$ [点拨]因为A⊕B = aA + bB,$n\otimes A=\underbrace{A\oplus A\oplus\cdots\oplus A}_{n个A}$,所以当a = 2,b = 1,A = x + y时,$n\otimes A=\underbrace{A\oplus A\oplus\cdots\oplus A}_{n个A}=\underbrace{(2A + A)\oplus A\oplus A\oplus\cdots\oplus A}_{(n - 2)个A}=3A\oplus\underbrace{A\oplus A\oplus\cdots\oplus A}_{(n - 2)个A}=\underbrace{(2×3A + A)\oplus A\oplus A\oplus\cdots\oplus A}_{(n - 3)个A}=7A\oplus\underbrace{A\oplus A\oplus\cdots\oplus A}_{(n - 3)个A}=\underbrace{(2×7A + A)\oplus A\oplus A\oplus\cdots\oplus A}_{(n - 4)个A}=15A\oplus\underbrace{A\oplus A\oplus\cdots\oplus A}_{(n - 4)个A}=\cdots=(2^{n}-1)A=(2^{n}-1)(x + y)$.
(2)由
(1)②知$P = n\otimes A=(2^{n}-1)A$,$Q = 3\otimes B=(2^{3}-1)B = 7B$.因为A = 2x² - y,B = x²+18y,所以P⊕Q = 2P + Q = 2(2^{n}-1)A + 7B =(2^{n + 1}-2)A + 7B =(2^{n + 1}-2)(2x² - y)+7(x²+18y)=(2^{n + 2}+3)x²+(128 - 2^{n + 1})y.因为P⊕Q的值与y的取值无关，所以128 - 2^{n + 1}=0,所以n = 6.