《2025年综合应用创新题典中点六年级数学上册鲁教版五四制》

10. [2025·聊城月考] 某市制定如下水费标准：若每户每月用水不超过 $ 10 $ m^3,则按 $ 2 $ 元/m^3 的水价收费,并加收 $ 0.3 $ 元/m^3 的污水处理费；若超过 $ 10 $ m^3,则超过的部分按 $ 3 $ 元/m^3 的水价收费,污水处理费不变.
(1)18.4 若小华家 $ 5 $ 月份的用水量为 $ 8 $ m^3,那么小华家 $ 5 $ 月份的水费为 ______ 元.
(2) 若小华家 $ 6 $ 月份的用水量为 $ 15 $ m^3,那么小华家 $ 6 $ 月份的水费为多少元?
(3) 若小华家某个月的用水量为 $ a(a ＞ 10) $ m^3,求小华家这个月的水费.(用含 $ a $ 的代数式表示)

答案： 【解】
(1)18.4
(2)由题意，得$10×(2+0.3)+(15-10)×(3+0.3)=39.5$(元).
答：小华家6月份的水费为39.5元.
(3)由题意，得$10×(2+0.3)+(a-10)(3+0.3)=(3.3a-10)$(元).
答：小华家这个月的水费为$(3.3a-10)$元.

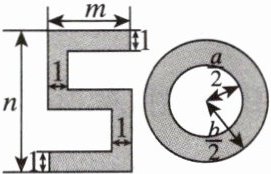
11. [2025·德州模拟] 在某中学一年一度的艺术节中,七年级某位同学设计了下面“50”的字样. “”的宽度均为 $ 1 $.
(1) 用含 $ a $,$ b $ 的式子表示圆环的周长；
(2) 用含 $ m $,$ n $ 的式子表示“”中阴影部分的面积.
]

答案： 【解】
(1)由题图可得，圆环的周长为$2\pi\cdot\frac{a}{2}+2\pi\cdot\frac{b}{2}=\pi a+\pi b$.
(2)由题意，得$S_{阴影}=1\cdot(m-1)+1\cdot n+1\cdot(m-1)+1\cdot(m-1)=m-1+n+m-1+m-1=3m+n-3$.

12.某超市出售一种商品,其原价为 $ a $ 元,现有三种调价方案：
① 先提价 $ 20\% $,再降价 $ 20\% $；
② 先降价 $ 20\% $,再提价 $ 20\% $；
③ 先提价 $ 15\% $,再降价 $ 15\% $.
问这三种方案的调价结果是否一样？最后是不是都恢复了原价？

答案： 【解】由题意，得①中的调价结果是$a(1+20\%)×(1-20\%)=0.96a$；②中的调价结果是$a(1-20\%)×(1+20\%)=0.96a$；③中的调价结果是$a(1+15\%)×(1-15\%)=0.9775a$.由上可知，三种方案的调价结果不都一样，最后都没有恢复原价.

13. 已知甲、乙两个油桶中各装有 $ a $ 升油.
(1) 把甲油桶中的油倒出一半装入乙油桶,现在乙油桶中装有多少升油？(用含 $ a $ 的代数式表示)
(2) 在 (1) 的前提下,再把乙油桶中的油倒出 $ \dfrac{1}{3} $ 装入甲油桶,最后甲、乙两个油桶中的油一样多吗？请说明理由.
]

答案： 【解】
(1)$a+\frac{1}{2}a=\frac{3}{2}a$(升).
答：现在乙油桶中装有$\frac{3}{2}a$升油.
(2)最后甲、乙两个油桶中的油一样多.理由如下：由
(1)可知甲油桶中现在装有$\frac{1}{2}a$升油，乙油桶中现在装有$\frac{3}{2}a$升油，若再把乙油桶中的油倒出$\frac{1}{3}$装入甲油桶，则甲油桶最后装有$\frac{1}{2}a+\frac{1}{3}×\frac{3}{2}a=a$(升)油，乙油桶最后装有$\frac{3}{2}a×(1-\frac{1}{3})=a$(升)油，故最后甲、乙两个油桶中的油一样多.