第100页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. [2024·济宁]如图,用大小相等的小正方形按照一定规律拼正方形.第一幅图有1个正方形,第二幅图有5个正方形,第三幅图有14个正方形……按照此规律,第六幅图中正方形的个数为(

A.90
B.91
C.92
D.93
B
)
A.90
B.91
C.92
D.93
答案:
B
2. 新考向 传统文化 围棋源自中国,围棋中棋子与棋盘体现出古代“天圆地方”的东方哲学.下列棋局都是由同样大小的黑棋、白棋按一定规律组成的,其中第①个图形中黑棋、白棋一共有9个,第②个图形中黑棋、白棋一共有14个,第③个图形中黑棋、白棋一共有19个,…,按此规律排列,则第⑧个图形中黑棋、白棋的总个数为(

A.36
B.40
C.44
D.48
C
)
A.36
B.40
C.44
D.48
答案:
C 【点拨】第①个图形中黑棋、白棋一共有3×4-4+1=9(个),第②个图形中黑棋、白棋一共有4×4-4+2=14(个),第③个图形中黑棋、白棋一共有5×4-4+3=19(个),…,按此规律排列,则第⑧个图形中黑棋、白棋的总个数为10×4-4+8=44(个),故选C.
3. 新考向 传统文化 如图①所示的中国结是我国特有的手工编织品,它是按照一定的规律编制而成的,如图②是其抽离出的平面图形,若其中第①个图形中共有9个小正方形,第②个图形中共有14个小正方形,第③个图形中共有19个小正方形,…;则第50个图形中小正方形的个数为(

A.245
B.246
C.254
D.255
C
)
A.245
B.246
C.254
D.255
答案:
C 【点拨】第①个图形中小正方形的个数为9=4+5×1,第②个图形中小正方形的个数为14=4+5×2,第③个图形中小正方形的个数为19=4+5×3,…,依此类推,第n个图形中小正方形的个数为4+5n,所以第50个图形中小正方形的个数为4+5×50=254.故选C.
4. [2025·日照岚山区期末]如图,将图①中的正方形剪开得到图②,图②中共有4个正方形;将图②上方的一个正方形剪开得到图③,图③中共有7个正方形;将图③上方的一个正方形剪开得到图④,图④中共有10个正方形;…;如此下去,则第2026个图形中正方形的总个数为(

A.6072
B.6074
C.6076
D.6078
6076
)
A.6072
B.6074
C.6076
D.6078
答案:
C 【点拨】由所给图形可知,图①中正方形的总个数为1=1×3-2,图②中正方形的总个数为4=2×3-2,图③中正方形的总个数为7=3×3-2,图④中正方形的总个数为10=4×3-2,…,依此类推,第n个图形中正方形的总个数为3n-2.当n=2026时,3n-2=3×2026-2=6076,即第2026个图形中正方形的总个数为6076.
5. 如图,古希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:称图中的数1,5,12,22…为五边形数,则第7个五边形数是(
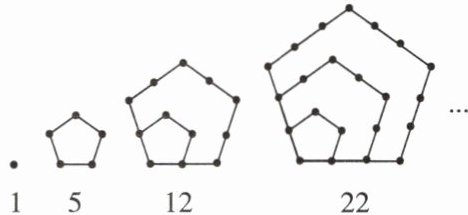
A.62
B.70
C.84
D.108
70
)
A.62
B.70
C.84
D.108
答案:
B 【点拨】由图可知,第1个五边形数为1,第2个五边形数为1+4=5,第3个五边形数为1+4+7=12,第4个五边形数为1+4+7+10=22,观察规律,可得第7个五边形数为1+4+7+10+13+16+19=70.
6. [2025·淄博期末]如图是一组有规律的图案,它们是由正五角星和圆形镶嵌而成,第1个图案有6个圆形,第2个图案有11个圆形,第3个图案有16个圆形,…,依此规律,第n个图案有
]

(5n+1)
个圆形(用含n的代数式表示).]

答案:
(5n+1) 【点拨】第1个图案有5+1=6(个)圆形,第2个图案有2×5+1=11(个)圆形,第3个图案有3×5+1=16(个)圆形,…,依此规律,第n个图案有(5n+1)个圆形.
7. 如图①,把边长为1的等边三角形每边三等分,经其向外长出一个边长为原来三分之一的小等边三角形得到图②,称为一次“生长”.在图②上类似“生长”,得到图③.若一共“生长”n次,则得到的多边形的周长是
]
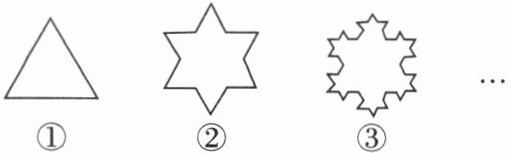
$3× \left(\frac{4}{3}\right)^n$
.]

答案:
$3× \left(\frac{4}{3}\right)^n$ 【点拨】观察图形发现,第一个图形的周长是3,经过一次“生长”的图形的周长是$3+3× \frac{1}{3}=3× \frac{4}{3}$;经过二次“生长”的图形的周长是$3× \frac{4}{3}+3× 4× \frac{1}{3}× \frac{1}{3}=3× \left(\frac{4}{3}\right)^2$;依此类推,则“生长”n次,得到的多边形的周长是$3× \left(\frac{4}{3}\right)^n$.
查看更多完整答案,请扫码查看


