第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
14. 有理数 $ a $,$ b $ 在数轴上对应点的位置如图所示,则下列结论正确的是(
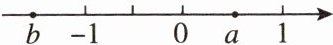
A.$ b - a > 0 $
B.$ |a| - |b| > 0 $
C.$ -b - a > 0 $
D.$ a + b > 0 $
C
)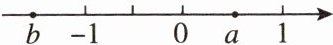
A.$ b - a > 0 $
B.$ |a| - |b| > 0 $
C.$ -b - a > 0 $
D.$ a + b > 0 $
答案:
C
15. 计算:
(1) $ (-30) - (-6) - (+6) - (-15) $;
(2) $ (-3\frac{2}{3}) - (-2\frac{3}{4}) - (+1\frac{2}{3}) - (+1.75) $.
(1) $ (-30) - (-6) - (+6) - (-15) $;
(2) $ (-3\frac{2}{3}) - (-2\frac{3}{4}) - (+1\frac{2}{3}) - (+1.75) $.
答案:
【解】
(1)原式=−30+6−6+15=−15.
(2)原式=−3$\frac{2}{3}$+2$\frac{3}{4}$−1$\frac{2}{3}$−1$\frac{3}{4}$=(−3$\frac{2}{3}$−1$\frac{2}{3}$)+(2$\frac{3}{4}$−1$\frac{3}{4}$)=−5$\frac{1}{3}$+1=−4$\frac{1}{3}$.
(1)原式=−30+6−6+15=−15.
(2)原式=−3$\frac{2}{3}$+2$\frac{3}{4}$−1$\frac{2}{3}$−1$\frac{3}{4}$=(−3$\frac{2}{3}$−1$\frac{2}{3}$)+(2$\frac{3}{4}$−1$\frac{3}{4}$)=−5$\frac{1}{3}$+1=−4$\frac{1}{3}$.
16. [2025·菏泽模拟] 设 $ A $ 是 $ -4 $ 的相反数与 $ -12 $ 的绝对值的差,$ B $ 是比 $ -6 $ 大 $ 5 $ 的数.
(1)求 $ A - B $.
(2)求 $ B - A $.
(3)从(1)与(2)的计算结果中,你能知道 $ A - B $ 与 $ B - A $ 有什么关系吗?
(1)求 $ A - B $.
(2)求 $ B - A $.
(3)从(1)与(2)的计算结果中,你能知道 $ A - B $ 与 $ B - A $ 有什么关系吗?
答案:
【解】因为A是−4的相反数与−12的绝对值的差,B是比−6大5的数,所以A=−(−4)−|−12|=4−12=−8,B=−6+5=−1.
(1)A−B=−8−(−1)=−8+1=−7.
(2)B−A=−1−(−8)=−1+8=7.
(3)A−B与B−A互为相反数.
(1)A−B=−8−(−1)=−8+1=−7.
(2)B−A=−1−(−8)=−1+8=7.
(3)A−B与B−A互为相反数.
17. 下表给出了某班 6 名同学的身高情况(单位:cm):

(1)将上面的表格填写完整.
(2)这 6 名同学中,身高最高的与最矮的相差多少?

(1)将上面的表格填写完整.
168;0;163;170;+6
(2)这 6 名同学中,身高最高的与最矮的相差多少?
172−163=9(cm). 答:这6名同学中,身高最高的与最矮的相差9cm.
答案:
【解】
(1)168;0;163;170;+6
(2)172−163=9(cm). 答:这6名同学中,身高最高的与最矮的相差9cm.
(1)168;0;163;170;+6
(2)172−163=9(cm). 答:这6名同学中,身高最高的与最矮的相差9cm.
18. 新视角 操作实践题 现有若干有理数排在多边形各边上,规定一次操作为:将任意相邻的两个数都减去同一个有理数,其余各数不变.如图①是小明两次操作的示意图,将三角形三边上的三个数变为了相同的数.
(1)将图②中三角形三边上的有理数都变为相同的数,并画出相应的操作示意图.(箭头上标注具体操作)
(2)如图③,若要将四边形的四条边上的四个数都变为相同的数,最少需要通过几次操作?给出你的判断,并画出相应的操作示意图.
(3)能否将 $ 2 $,$ 4 $,$ 6 $,$ 9 $ 这 $ 4 $ 个有理数以某种方式排列在四边形的四条边上,使得通过若干次操作将这 $ 4 $ 个有理数变为相同的数?如果能,请画出最初的排列方式与具体的操作步骤;如果不能,请说明理由.
]

(1)将图②中三角形三边上的有理数都变为相同的数,并画出相应的操作示意图.(箭头上标注具体操作)
(2)如图③,若要将四边形的四条边上的四个数都变为相同的数,最少需要通过几次操作?给出你的判断,并画出相应的操作示意图.
(3)能否将 $ 2 $,$ 4 $,$ 6 $,$ 9 $ 这 $ 4 $ 个有理数以某种方式排列在四边形的四条边上,使得通过若干次操作将这 $ 4 $ 个有理数变为相同的数?如果能,请画出最初的排列方式与具体的操作步骤;如果不能,请说明理由.
]

答案:
【解】
(1)如图①.
(2)若要将四边形的四条边上的四个数都变为相同的数,最少需要通过两次操作. 如果只进行一次操作,只能改变相邻的两个数,剩下的两个数不相等,因此最少需要通过两次操作. 操作示意图如图②所示.
(3)不能. 理由如下:因为2+4+6+9=21,21为奇数,所以操作一次,将相邻两个数都减去同一个数,其余数不变,易知得到的四个数的和仍为奇数. 因为最终得到四个相同的数,所以最终得到的四个数的和为偶数,所以不能将2,4,6,9这4个有理数以某种方式排列在四边形的四条边上,使得通过若干次操作将这4个有理数变为相同的数.
【解】
(1)如图①.

(2)若要将四边形的四条边上的四个数都变为相同的数,最少需要通过两次操作. 如果只进行一次操作,只能改变相邻的两个数,剩下的两个数不相等,因此最少需要通过两次操作. 操作示意图如图②所示.

(3)不能. 理由如下:因为2+4+6+9=21,21为奇数,所以操作一次,将相邻两个数都减去同一个数,其余数不变,易知得到的四个数的和仍为奇数. 因为最终得到四个相同的数,所以最终得到的四个数的和为偶数,所以不能将2,4,6,9这4个有理数以某种方式排列在四边形的四条边上,使得通过若干次操作将这4个有理数变为相同的数.
查看更多完整答案,请扫码查看


