第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
12. 请根据如图所示的对话解答下列问题.

(1)求 $ a $,$ b $,$ c $ 的值;
(2)求 $ 8 - a + b - c $ 的值.

(1)求 $ a $,$ b $,$ c $ 的值;
(2)求 $ 8 - a + b - c $ 的值.
答案:
【解】
(1)因为a的相反数是3,b<a,且b的绝对值是6,c+b=-8,所以a=-3,b=-6,c=-2.
(2)因为a=-3,b=-6,c=-2,所以8-a+b-c=8-(-3)+(-6)-(-2)=8+3-6+2=7.
(1)因为a的相反数是3,b<a,且b的绝对值是6,c+b=-8,所以a=-3,b=-6,c=-2.
(2)因为a=-3,b=-6,c=-2,所以8-a+b-c=8-(-3)+(-6)-(-2)=8+3-6+2=7.
13. 已知 $ A = - 3 \frac { 1 } { 5 } - 2 \frac { 1 } { 7 } - 4 \frac { 4 } { 5 } - \left( - 5 \frac { 1 } { 7 } \right) $,$ B = 6 \frac { 1 } { 3 } + ( - 4.6 ) - 5.4 - \left( - 7 \frac { 2 } { 3 } \right) $.
(1)计算 $ A $,$ B $ 的值;
(2)将 $ A $,$ B $ 两数对应的点表示在如图所示的数轴上,并求 $ A $,$ B $ 两数对应的点之间的距离.
]
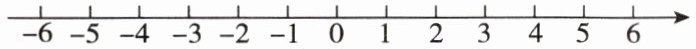
(1)计算 $ A $,$ B $ 的值;
(2)将 $ A $,$ B $ 两数对应的点表示在如图所示的数轴上,并求 $ A $,$ B $ 两数对应的点之间的距离.
]
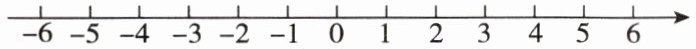
答案:
【解】
(1)$A=-3\frac{1}{5}-2\frac{1}{7}-4\frac{4}{5}-\left(-5\frac{1}{7}\right)$$=-3\frac{1}{5}-2\frac{1}{7}-4\frac{4}{5}+5\frac{1}{7}$$=\left(-3\frac{1}{5}-4\frac{4}{5}\right)+\left(5\frac{1}{7}-2\frac{1}{7}\right)$$=-8+3$$=-5$.$B=6\frac{1}{3}+(-4.6)-5.4-\left(-7\frac{2}{3}\right)$$=6\frac{1}{3}-4.6-5.4+7\frac{2}{3}$$=\left(6\frac{1}{3}+7\frac{2}{3}\right)-(4.6+5.4)$$=14-10$$=4$.
(2)将A,B两数对应的点表示在数轴上如图所示.-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 A,B两数对应的点之间的距离为4-(-5)=9.
(1)$A=-3\frac{1}{5}-2\frac{1}{7}-4\frac{4}{5}-\left(-5\frac{1}{7}\right)$$=-3\frac{1}{5}-2\frac{1}{7}-4\frac{4}{5}+5\frac{1}{7}$$=\left(-3\frac{1}{5}-4\frac{4}{5}\right)+\left(5\frac{1}{7}-2\frac{1}{7}\right)$$=-8+3$$=-5$.$B=6\frac{1}{3}+(-4.6)-5.4-\left(-7\frac{2}{3}\right)$$=6\frac{1}{3}-4.6-5.4+7\frac{2}{3}$$=\left(6\frac{1}{3}+7\frac{2}{3}\right)-(4.6+5.4)$$=14-10$$=4$.
(2)将A,B两数对应的点表示在数轴上如图所示.-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 A,B两数对应的点之间的距离为4-(-5)=9.
14. [新考法 阅读类比法] 在求 $ \frac { 1 } { 2 } + \left( \frac { 1 } { 3 } + \frac { 2 } { 3 } \right) + \left( \frac { 1 } { 4 } + \frac { 2 } { 4 } + \frac { 3 } { 4 } \right) + \left( \frac { 1 } { 5 } + \frac { 2 } { 5 } + \frac { 3 } { 5 } + \frac { 4 } { 5 } \right) $ 的结果时,小明发现,若调整各括号内加数的顺序再进行计算,便能很容易得到这些加数的和,具体方法如下:
假设 $ A = \frac { 1 } { 2 } + \left( \frac { 1 } { 3 } + \frac { 2 } { 3 } \right) + \left( \frac { 1 } { 4 } + \frac { 2 } { 4 } + \frac { 3 } { 4 } \right) + \left( \frac { 1 } { 5 } + \frac { 2 } { 5 } + \frac { 3 } { 5 } + \frac { 4 } { 5 } \right) $,①
又有 $ A = \frac { 1 } { 2 } + \left( \frac { 2 } { 3 } + \frac { 1 } { 3 } \right) + \left( \frac { 3 } { 4 } + \frac { 2 } { 4 } + \frac { 1 } { 4 } \right) + \left( \frac { 4 } { 5 } + \frac { 3 } { 5 } + \frac { 2 } { 5 } + \frac { 1 } { 5 } \right) $,②
①+②,得 $ 2 A = 1 + ( 1 + 1 ) + ( 1 + 1 + 1 ) + ( 1 + 1 + 1 + 1 ) = 1 + 2 + 3 + 4 = 10 $,
所以 $ A = 5 $,所以 $ \frac { 1 } { 2 } + \left( \frac { 1 } { 3 } + \frac { 2 } { 3 } \right) + \left( \frac { 1 } { 4 } + \frac { 2 } { 4 } + \frac { 3 } { 4 } \right) + \left( \frac { 1 } { 5 } + \frac { 2 } { 5 } + \frac { 3 } { 5 } + \frac { 4 } { 5 } \right) = 5 $.
计算:$ \frac { 1 } { 2 } - \left( \frac { 1 } { 3 } + \frac { 2 } { 3 } \right) + \left( \frac { 1 } { 4 } + \frac { 2 } { 4 } + \frac { 3 } { 4 } \right) - \left( \frac { 1 } { 5 } + \frac { 2 } { 5 } + \frac { 3 } { 5 } + \frac { 4 } { 5 } \right) + … - \left( \frac { 1 } { 2 025 } + \frac { 2 } { 2 025 } + … + \frac { 2 024 } { 2 025 } \right) $.
]
假设 $ A = \frac { 1 } { 2 } + \left( \frac { 1 } { 3 } + \frac { 2 } { 3 } \right) + \left( \frac { 1 } { 4 } + \frac { 2 } { 4 } + \frac { 3 } { 4 } \right) + \left( \frac { 1 } { 5 } + \frac { 2 } { 5 } + \frac { 3 } { 5 } + \frac { 4 } { 5 } \right) $,①
又有 $ A = \frac { 1 } { 2 } + \left( \frac { 2 } { 3 } + \frac { 1 } { 3 } \right) + \left( \frac { 3 } { 4 } + \frac { 2 } { 4 } + \frac { 1 } { 4 } \right) + \left( \frac { 4 } { 5 } + \frac { 3 } { 5 } + \frac { 2 } { 5 } + \frac { 1 } { 5 } \right) $,②
①+②,得 $ 2 A = 1 + ( 1 + 1 ) + ( 1 + 1 + 1 ) + ( 1 + 1 + 1 + 1 ) = 1 + 2 + 3 + 4 = 10 $,
所以 $ A = 5 $,所以 $ \frac { 1 } { 2 } + \left( \frac { 1 } { 3 } + \frac { 2 } { 3 } \right) + \left( \frac { 1 } { 4 } + \frac { 2 } { 4 } + \frac { 3 } { 4 } \right) + \left( \frac { 1 } { 5 } + \frac { 2 } { 5 } + \frac { 3 } { 5 } + \frac { 4 } { 5 } \right) = 5 $.
计算:$ \frac { 1 } { 2 } - \left( \frac { 1 } { 3 } + \frac { 2 } { 3 } \right) + \left( \frac { 1 } { 4 } + \frac { 2 } { 4 } + \frac { 3 } { 4 } \right) - \left( \frac { 1 } { 5 } + \frac { 2 } { 5 } + \frac { 3 } { 5 } + \frac { 4 } { 5 } \right) + … - \left( \frac { 1 } { 2 025 } + \frac { 2 } { 2 025 } + … + \frac { 2 024 } { 2 025 } \right) $.
]
答案:
【解】设$M=\frac{1}{2}-\left(\frac{1}{3}+\frac{2}{3}\right)+\left(\frac{1}{4}+\frac{2}{4}+\frac{3}{4}\right)-\left(\frac{1}{5}+\frac{2}{5}+\frac{3}{5}+\frac{4}{5}\right)+\cdots -\left(\frac{1}{2025}+\frac{2}{2025}+\cdots +\frac{2024}{2025}\right)$,①又有$M=\frac{1}{2}-\left(\frac{2}{3}+\frac{1}{3}\right)+\left(\frac{3}{4}+\frac{2}{4}+\frac{1}{4}\right)-\left(\frac{4}{5}+\frac{3}{5}+\frac{2}{5}+\frac{1}{5}\right)+\cdots -\left(\frac{2024}{2025}+\frac{2023}{2025}+\cdots +\frac{2}{2025}+\frac{1}{2025}\right)$,②①+②,得$2M=1-(1+1)+(1+1+1)-(1+1+1+1)+\cdots -\underbrace{(1+1+\cdots +1)}_{共2024个1}$$=1-2+3-4+\cdots -2024$$=\underbrace{-1-1-1-\cdots -1}_{共1012个-1}$$=-1012$.所以$M=-\frac{1012}{2}$,所以$\frac{1}{2}-\left(\frac{1}{3}+\frac{2}{3}\right)+\left(\frac{1}{4}+\frac{2}{4}+\frac{3}{4}\right)-\left(\frac{1}{5}+\frac{2}{5}+\frac{3}{5}+\frac{4}{5}\right)+\cdots -\left(\frac{1}{2025}+\frac{2}{2025}+\cdots +\frac{2024}{2025}\right)=-\frac{1012}{2}$.
查看更多完整答案,请扫码查看


