第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
12. 在如图所示的数轴上,$(-5)÷\vert -2\vert÷\left(-6\dfrac{1}{4}\right)$的值对应的点是(

A.$M$
B.$N$
C.$P$
D.$Q$
C
)
A.$M$
B.$N$
C.$P$
D.$Q$
答案:
C
13. 若两个数的商为$-1$,则这两个数(
A.都是$1$
B.都是$-1$
C.是一对倒数
D.是一对非零相反数
D
)A.都是$1$
B.都是$-1$
C.是一对倒数
D.是一对非零相反数
答案:
D
14. 有理数$a$,$b$,$c$在数轴上对应的点如图所示,则下列各式正确的有(
①$abc\gt0$;②$b - a + c\lt0$;③$\vert a + b\vert = a + b$;
④$\dfrac{1}{c}\gt\dfrac{1}{a}$;⑤$\dfrac{-2\vert b\vert}{b}= -2$.
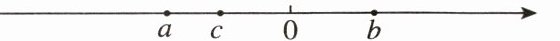
A.$1$个
B.$2$个
C.$3$个
D.$4$个
B
)①$abc\gt0$;②$b - a + c\lt0$;③$\vert a + b\vert = a + b$;
④$\dfrac{1}{c}\gt\dfrac{1}{a}$;⑤$\dfrac{-2\vert b\vert}{b}= -2$.
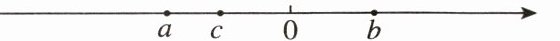
A.$1$个
B.$2$个
C.$3$个
D.$4$个
答案:
B 【点拨】由数轴知$a\lt c<0\lt b,|c|<|b|<|a|$,所以$abc>0,b-a+c>0,a+b<0,\frac{-2|b|}{b}=\frac{-2b}{b}=-2,\frac{1}{c}<\frac{1}{a}$,所以$|a+b|=-a-b$,所以正确的有①⑤,故选 B.
15. [2025·济南月考]“冬至”是一年中白昼最短、黑夜最长的一天.这天,济南的白昼时间是黑夜时间的$\dfrac{5}{7}$,而“中国最北端”漠河县的白昼时间是黑夜时间的$\dfrac{1}{2}$,“冬至”这一天,济南的黑夜时间是漠河黑夜时间的
$\frac{7}{8}$
.(填分数)
答案:
$\frac{7}{8}$
16. [2025·泰安月考]对于有理数$x$,$y$,若$\dfrac{x}{y}\lt0$,则$\dfrac{\vert xy\vert}{xy}+\dfrac{y}{\vert y\vert}+\dfrac{\vert x\vert}{x}$的值是
-1
。
答案:
-1 【点拨】因为$\frac{x}{y}<0$,所以x,y异号.所以$xy<0$.所以$\frac{|xy|}{xy}=\frac{-xy}{xy}=-1$.当$x>0$时,$y<0$,则$\frac{y}{|y|}=\frac{y}{-y}=-1,\frac{|x|}{x}=\frac{x}{x}=1$,所以原式$=-1+(-1)+1=-1$.当$x<0$时,$y>0$,则$\frac{y}{|y|}=\frac{y}{y}=1,\frac{|x|}{x}=\frac{-x}{x}=-1$,所以原式$=-1+1-1=-1$.综上,$\frac{|xy|}{xy}+\frac{y}{|y|}+\frac{|x|}{x}=-1$.
17. 新视角 过程探究题 小华在课外书中看到这样一道题:
计算:$\dfrac{1}{36}÷\left(\dfrac{1}{4}+\dfrac{1}{12}-\dfrac{7}{18}-\dfrac{1}{36}\right)+\left(\dfrac{1}{4}+\dfrac{1}{12}-\dfrac{7}{18}-\dfrac{1}{36}\right)÷\dfrac{1}{36}$.
她发现,这个算式求的是前、后两部分的和,而这两部分之间存在着某种关系,利用这种关系,她顺利地解答了这道题.
(1)前、后两部分之间存在着什么关系?
(2)先计算哪部分比较简便?并计算比较简便的那部分.
(3)利用(1)中的关系,直接写出另一部分的结果.
(4)根据以上分析,求出原式的结果.
计算:$\dfrac{1}{36}÷\left(\dfrac{1}{4}+\dfrac{1}{12}-\dfrac{7}{18}-\dfrac{1}{36}\right)+\left(\dfrac{1}{4}+\dfrac{1}{12}-\dfrac{7}{18}-\dfrac{1}{36}\right)÷\dfrac{1}{36}$.
她发现,这个算式求的是前、后两部分的和,而这两部分之间存在着某种关系,利用这种关系,她顺利地解答了这道题.
(1)前、后两部分之间存在着什么关系?
(2)先计算哪部分比较简便?并计算比较简便的那部分.
(3)利用(1)中的关系,直接写出另一部分的结果.
(4)根据以上分析,求出原式的结果.
答案:
【解】
(1)前、后两部分互为倒数.
(2)先计算后一部分比较简便.
$(\frac{1}{4}+\frac{1}{12}-\frac{7}{18}-\frac{1}{36})÷ \frac{1}{36}$
$=(\frac{1}{4}+\frac{1}{12}-\frac{7}{18}-\frac{1}{36})× 36$
$=9+3-14-1=-3.$
(3)因为前、后两部分互为倒数,所以$\frac{1}{36}÷ (\frac{1}{4}+\frac{1}{12}-\frac{7}{18}-\frac{1}{36})=-\frac{1}{3}.$
(4)原式$=-\frac{1}{3}+(-3)=-3\frac{1}{3}.$
(1)前、后两部分互为倒数.
(2)先计算后一部分比较简便.
$(\frac{1}{4}+\frac{1}{12}-\frac{7}{18}-\frac{1}{36})÷ \frac{1}{36}$
$=(\frac{1}{4}+\frac{1}{12}-\frac{7}{18}-\frac{1}{36})× 36$
$=9+3-14-1=-3.$
(3)因为前、后两部分互为倒数,所以$\frac{1}{36}÷ (\frac{1}{4}+\frac{1}{12}-\frac{7}{18}-\frac{1}{36})=-\frac{1}{3}.$
(4)原式$=-\frac{1}{3}+(-3)=-3\frac{1}{3}.$
18. 我们知道,在数学学习中,分类讨论是一种重要的数学思想,能使思维更加严谨和全面.请你运用所学知识,解答下面的问题:
(1)若$a$,$b$都是有理数,$\vert a\vert =3$,$\vert b\vert =7$,且$a\lt b$,求$a + b$的值.
(2)若$a$,$b$都是非零的有理数,且满足$a$,$b$同号,求$\dfrac{\vert a\vert}{a}+\dfrac{\vert b\vert}{b}$的值.
(3)若$a$,$b$,$c$都是有理数,且$a× b× c\gt0$,求$\dfrac{\vert a\vert}{a}+\dfrac{\vert b\vert}{b}+\dfrac{\vert c\vert}{c}$的值.
(1)若$a$,$b$都是有理数,$\vert a\vert =3$,$\vert b\vert =7$,且$a\lt b$,求$a + b$的值.
(2)若$a$,$b$都是非零的有理数,且满足$a$,$b$同号,求$\dfrac{\vert a\vert}{a}+\dfrac{\vert b\vert}{b}$的值.
(3)若$a$,$b$,$c$都是有理数,且$a× b× c\gt0$,求$\dfrac{\vert a\vert}{a}+\dfrac{\vert b\vert}{b}+\dfrac{\vert c\vert}{c}$的值.
答案:
【解】
(1)因为a,b都是有理数,$|a|=3,|b|=7$,且$a\lt b$,所以$a=3,b=7$或$a=-3,b=7$.当$a=3,b=7$时,$a+b=3+7=10$;当$a=-3,b=7$时,$a+b=-3+7=4$.综上,$a+b$的值是 10 或 4.
(2)因为a,b都是非零的有理数,且满足a,b同号,所以$a>0,b>0$或$a<0,b<0$.当$a>0,b>0$时,$\frac{|a|}{a}+\frac{|b|}{b}=\frac{a}{a}+\frac{b}{b}=1+1=2$;当$a<0,b<0$时,$\frac{|a|}{a}+\frac{|b|}{b}=\frac{-a}{a}+\frac{-b}{b}=-1+(-1)=-2$.综上,$\frac{|a|}{a}+\frac{|b|}{b}$的值为 2 或-2.
(3)因为a,b,c都是有理数,且$a× b× c>0$,所以a,b,c均为正数或为一正两负.当a,b,c均为正数,即$a>0,b>0,c>0$时,$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}=\frac{a}{a}+\frac{b}{b}+\frac{c}{c}=1+1+1=3$;当a,b,c为一正两负时,不妨设$a>0,b<0,c<0$,则$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}=\frac{a}{a}+\frac{-b}{b}+\frac{-c}{c}=1+(-1)+(-1)=-1$.综上,$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}$的值是 3 或-1.
(1)因为a,b都是有理数,$|a|=3,|b|=7$,且$a\lt b$,所以$a=3,b=7$或$a=-3,b=7$.当$a=3,b=7$时,$a+b=3+7=10$;当$a=-3,b=7$时,$a+b=-3+7=4$.综上,$a+b$的值是 10 或 4.
(2)因为a,b都是非零的有理数,且满足a,b同号,所以$a>0,b>0$或$a<0,b<0$.当$a>0,b>0$时,$\frac{|a|}{a}+\frac{|b|}{b}=\frac{a}{a}+\frac{b}{b}=1+1=2$;当$a<0,b<0$时,$\frac{|a|}{a}+\frac{|b|}{b}=\frac{-a}{a}+\frac{-b}{b}=-1+(-1)=-2$.综上,$\frac{|a|}{a}+\frac{|b|}{b}$的值为 2 或-2.
(3)因为a,b,c都是有理数,且$a× b× c>0$,所以a,b,c均为正数或为一正两负.当a,b,c均为正数,即$a>0,b>0,c>0$时,$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}=\frac{a}{a}+\frac{b}{b}+\frac{c}{c}=1+1+1=3$;当a,b,c为一正两负时,不妨设$a>0,b<0,c<0$,则$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}=\frac{a}{a}+\frac{-b}{b}+\frac{-c}{c}=1+(-1)+(-1)=-1$.综上,$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}$的值是 3 或-1.
查看更多完整答案,请扫码查看


