《2025年综合应用创新题典中点六年级数学上册鲁教版五四制》

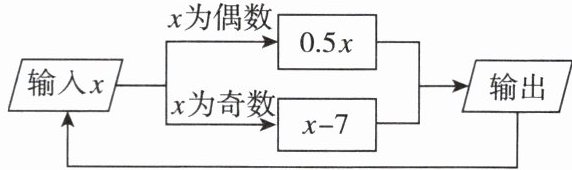
10. 新考向 数学文化 程序框图的算法思路源于我国古代数学名著《九章算术》,如图所示的程序框图,当输入的$x$的值是20时,根据程序计算,第1次输出的结果为10,第2次输出的结果为5,…,这样下去,第2025次输出的结果为(C)

A.$-2$
B.$-1$
C.$-8$
D.$-4$

答案： C　【点拨】由题意知，第1次输出的结果为10，第2次输出的结果为5，第3次输出的结果为−2，第4次输出的结果为−1，第5次输出的结果为−8，第6次输出的结果为−4，第7次输出的结果为−2，第8次输出的结果为−1，第9次输出的结果为−8，...，这列数除前2个数外，每4个数为一个循环，即为−2，−1，−8，−4.因为(2025−2)÷4=505......3，所以第2025次输出的结果是−8.故选C.

11. 如图,数轴上$A$,$B$两点之间的距离为1个单位长度,$B$,$C$两点之间的距离为3个单位长度。现有一动点$P从点A$开始沿该数轴的正方向运动,到达点$C$停止。若在运动的过程中,点$P到A$,$B$,$C三点的距离之和的最大值为m$,最小值为$n$,则$(-m)^{n}$的值为( )


A.$-2401$
B.$-625$
C.625
D.2401

答案：
D　【点拨】当点P在线段AB上(0≤PB≤1)时，如图①，

所以PA+PB+PC=AB+(PB+BC)=1+PB+3=4+PB.因为0≤PB≤1，所以4≤PA+PB+PC≤5；当点P在线段BC上(0＜PB≤3)时，如图②，

所以PA+PB+PC=(AB+BP)+BC=1+PB+3=4+PB.因为0＜PB≤3，所以4＜PA+PB+PC≤7.综上，4≤PA+PB+PC≤7.所以点P到A，B，C三点的距离之和的最大值为m=7，最小值为n=4.所以(−m)ⁿ=(−7)⁴=2401.

12. 先阅读下面例题的解答过程,再回答后面的问题。
例：已知代数式$6y + 4y^{2}$的值为2,求$2y^{2}+3y + 7$的值。
解：由$6y + 4y^{2}= 2$,得$3y + 2y^{2}= 1$,所以$2y^{2}+3y + 7 = 1 + 7 = 8$。
(1)已知代数式$2a^{2}+3b$的值为6,求$a^{2}+\frac{3}{2}b - 5$的值；
(2)已知代数式$14x + 5 - 21x^{2}的值为-2$,求$6x^{2}-4x + 5$的值。

答案： 【解】
(1)由2a²+3b=6，得a²+$\frac{3}{2}$b=3，所以a²+$\frac{3}{2}$b−5=3−5=−2.
(2)因为14x+5−21x²的值为−2，所以14x−21x²=−7.所以2x−3x²=−1.所以3x²−2x=1.所以6x²−4x+5=2×(3x²−2x)+5=2×1+5=7.

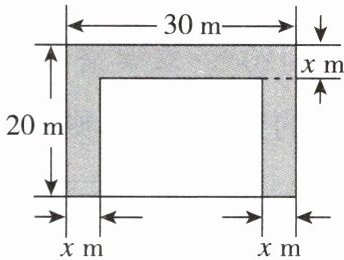
13. 情境题 方案设计型 某中学有一块长30m、宽20m的长方形空地,计划在这块空地上划分出部分区域种花,小明同学的设计方案如图(阴影部分为种花区域),设种花区域的宽度为$x$m。
(1)请用含$x$的式子表示空白部分的面积。
(2)当$x = 2$时,空白部分的面积是否超过400$m^{2}$？请说明理由。
]

答案： 【解】
(1)空白部分的面积为(30−2x)(20−x)m².
(2)当x=2时，空白部分的面积超过了400m².理由如下：当x=2时，(30−2x)(20−x)=(30−2×2)×(20−2)=468.因为468m²＞400m²，所以空白部分的面积超过了400m².

14. 新考法 规律探究法 试探索代数式$a^{2}-2ab + b^{2}与(a - b)^{2}$的关系。
(1)当$a = 2$,$b= -1$时,分别求代数式$a^{2}-2ab + b^{2}与(a - b)^{2}$的值。
(2)当$a= -\frac{1}{2}$,$b = 2$时,分别求代数式$a^{2}-2ab + b^{2}与(a - b)^{2}$的值。
(3)从上述计算中,你发现了什么规律？当$a = 2027$,$b = 2025$时,请利用你发现的规律求代数式$a^{2}-2ab + b^{2}$的值。
]

答案： 【解】
(1)当a=2，b=−1时，a²−2ab+b²=2²−2×2×(−1)+(−1)²=9，(a−b)²=[2−(−1)]²=3²=9.
(2)当a=−$\frac{1}{2}$，b=2时，a²−2ab+b²=(−$\frac{1}{2}$)²−2×(−$\frac{1}{2}$)×2+2²=$\frac{25}{4}$，(a−b)²=(−$\frac{1}{2}$−2)²=(−$\frac{5}{2}$)²=$\frac{25}{4}$.
(3)规律：a²−2ab+b²=(a−b)².当a=2027，b=2025时，a²−2ab+b²=(a−b)²=(2027−2025)²=2²=4.