第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
10. 两个圆柱的底面半径均为30cm,高均为50cm,将这两个圆柱的侧面展开图粘成一个大的矩形(不重叠),然后再将它卷成与原来圆柱等高的圆柱的侧面,求新卷成的圆柱的体积。(结果保留π)
答案:
【解】因为两个圆柱的底面半径均为30cm,高均为50cm,所以它们的侧面展开图的长是2π×30 = 60π(cm),所以新卷成的圆柱的侧面的长为120πcm.设新卷成的圆柱的底面半径为rcm,则2πr = 120π,解得r = 60.所以新卷成的圆柱的体积为πr²×50 = 3600π×50 = 180000π(cm³).
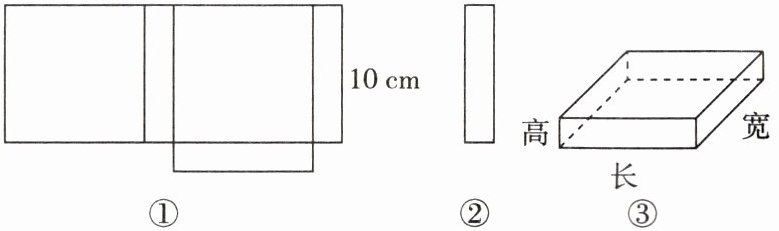
11. 小明学习了正方体的展开图后,明白了很多几何体都能展开成平面图形。于是他在家用剪刀剪开了一个长方体纸盒,可是一不小心多剪开了一条棱,把纸盒剪成了两部分,如图①、图②所示。请根据你所学的知识,回答下列问题:
(1)【动手操作】
现在小明想将剪断的图②重新粘贴到图①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒(如图③),请你帮助小明在图①中补全图形(补出来一种即可);
(2)【解决问题】
经过测量,小明发现这个纸盒的底面是一个正方形,它的边长是长方体高的5倍,根据图①中的数据,求这个纸盒的体积。
(1)【动手操作】
现在小明想将剪断的图②重新粘贴到图①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒(如图③),请你帮助小明在图①中补全图形(补出来一种即可);
(2)【解决问题】
经过测量,小明发现这个纸盒的底面是一个正方形,它的边长是长方体高的5倍,根据图①中的数据,求这个纸盒的体积。

答案:
【解】
(1)如图,有四种补法,任选其一即可. ①
①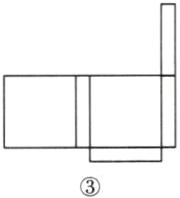
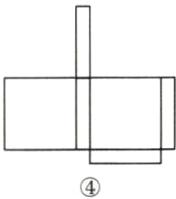
(2)由题图知,长方体底面正方形的边长为10cm.因为正方形边长是长方体高的5倍,所以长方体高为2cm.所以这个纸盒的体积为10×10×2 = 200(cm³).
【解】
(1)如图,有四种补法,任选其一即可.
 ①
①

(2)由题图知,长方体底面正方形的边长为10cm.因为正方形边长是长方体高的5倍,所以长方体高为2cm.所以这个纸盒的体积为10×10×2 = 200(cm³).
12. 新视角 操作实践题 某综合实践小组开展了“长方体纸盒的制作”实践活动,他们利用边长为a cm的正方形纸板制作出两种不同的长方体纸盒(图①为无盖的长方体纸盒,图②为有盖的长方体纸盒)。
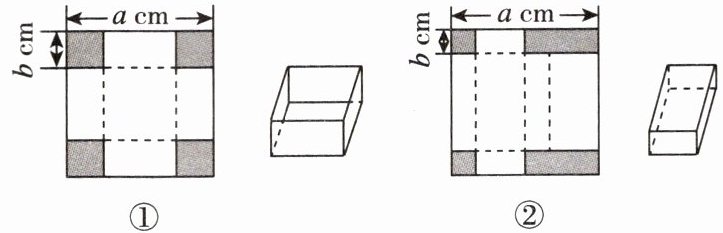
【操作一】根据图①方式制作一个无盖的长方体纸盒。方法:先在纸板四角剪去四个同样大小且边长为b cm的小正方形,再沿虚线折起来。
【问题解决】
(1)若$a = 12$,$b = 3$,则长方体纸盒的底面积为
【操作二】根据图②方式制作一个有盖的长方体纸盒。方法:先在纸板四角剪去两个同样大小且边长为b cm的小正方形和两个同样大小的小长方形,再沿虚线折起来。
【拓展延伸】
(2)若$a = 12$,$b = 2$,则该长方体纸盒的体积为
(3)现有两张边长为a cm的正方形纸板,分别按图①、图②的要求制作无盖和有盖的两个长方体纸盒,若$a = 30$,$b = 5$,求无盖纸盒的体积是有盖纸盒体积的多少倍。

【操作一】根据图①方式制作一个无盖的长方体纸盒。方法:先在纸板四角剪去四个同样大小且边长为b cm的小正方形,再沿虚线折起来。
【问题解决】
(1)若$a = 12$,$b = 3$,则长方体纸盒的底面积为
36cm²
。【操作二】根据图②方式制作一个有盖的长方体纸盒。方法:先在纸板四角剪去两个同样大小且边长为b cm的小正方形和两个同样大小的小长方形,再沿虚线折起来。
【拓展延伸】
(2)若$a = 12$,$b = 2$,则该长方体纸盒的体积为
64cm³
。(3)现有两张边长为a cm的正方形纸板,分别按图①、图②的要求制作无盖和有盖的两个长方体纸盒,若$a = 30$,$b = 5$,求无盖纸盒的体积是有盖纸盒体积的多少倍。
当a = 30,b = 5时,按题图①制作的无盖长方体纸盒的体积为(30 - 5×2)×(30 - 5×2)×5 = 2000(cm³).按题图②制作的有盖长方体纸盒的体积为(30 - 5×2)×($\frac{30 - 5×2}{2}$)×5 = 1000(cm³).因为2000÷1000 = 2,所以无盖纸盒的体积是有盖纸盒体积的2倍.
答案:
(1)36cm²
(2)64cm³ 【点拨】如题图②,先在纸板四角剪去两个同样大小且边长为bcm的小正方形和两个同样大小的小长方形,再沿虚线折起来可得到长为(a - 2b)cm,宽为$\frac{a - 2b}{2}$cm,高为bcm的长方体.当a = 12,b = 2时,该长方体纸盒的长为12 - 2×2 = 8(cm),宽为$\frac{12 - 2×2}{2}$ = 4(cm),高为2cm,所以体积为8×4×2 = 64(cm³).
(3)当a = 30,b = 5时,按题图①制作的无盖长方体纸盒的体积为(30 - 5×2)×(30 - 5×2)×5 = 2000(cm³).按题图②制作的有盖长方体纸盒的体积为(30 - 5×2)×($\frac{30 - 5×2}{2}$)×5 = 1000(cm³).因为2000÷1000 = 2,所以无盖纸盒的体积是有盖纸盒体积的2倍.
(1)36cm²
(2)64cm³ 【点拨】如题图②,先在纸板四角剪去两个同样大小且边长为bcm的小正方形和两个同样大小的小长方形,再沿虚线折起来可得到长为(a - 2b)cm,宽为$\frac{a - 2b}{2}$cm,高为bcm的长方体.当a = 12,b = 2时,该长方体纸盒的长为12 - 2×2 = 8(cm),宽为$\frac{12 - 2×2}{2}$ = 4(cm),高为2cm,所以体积为8×4×2 = 64(cm³).
(3)当a = 30,b = 5时,按题图①制作的无盖长方体纸盒的体积为(30 - 5×2)×(30 - 5×2)×5 = 2000(cm³).按题图②制作的有盖长方体纸盒的体积为(30 - 5×2)×($\frac{30 - 5×2}{2}$)×5 = 1000(cm³).因为2000÷1000 = 2,所以无盖纸盒的体积是有盖纸盒体积的2倍.
查看更多完整答案,请扫码查看


