《2025年综合应用创新题典中点六年级数学上册鲁教版五四制》

1. 按照一定规律排列的式子：$\frac{x^{2}}{3}, \frac{x^{4}}{5}, \frac{x^{6}}{7}, \frac{x^{8}}{9}, …$,第2026个式子是(C)
A.$\frac{x^{4054}}{4053}$
B.$\frac{x^{4054}}{4051}$
C.$\frac{x^{4052}}{4053}$
D.$\frac{x^{4052}}{4051}$

答案： C

2. 计算：$3^{1}= 3, 3^{2}= 9, 3^{3}= 27, …$归纳计算结果中的个位数字的规律,猜测$3^{2025}+2$的个位数字是(C)
A.1
B.3
C.5
D.9

答案： C

3. [2025·聊城实验中学月考]观察下列式子：
第1个式子：$3^{2}-4×1^{2}= 4×1+1；$
第2个式子：$5^{2}-4×2^{2}= 4×2+1；$
第3个式子：$7^{2}-4×3^{2}= 4×3+1；$
第4个式子：$9^{2}-4×4^{2}= 4×4+1。$
…请你按照上述规律,回答下列问题：(1)写出第5个式子：$11^{2}-4×5^{2}=4×5+1$；(2)写出第n个式子：$(2n+1)^{2}-4n^{2}=4n+1$(用含n的式子表示)；(3)请你按照规律计算$2025^{2}-4×1012^{2}$的值。
当$n=1012$时,$2n+1=2025,$所以$2025^{2}-4×1012^{2}=4×1012+1=4049.$

答案： 【解】
(1)$11^{2}-4×5^{2}=4×5+1$
(2)$(2n+1)^{2}-4n^{2}=4n+1$
(3)当$n=1012$时,$2n+1=2025,$所以$2025^{2}-4×1012^{2}=4×1012+1=4049.$

4. [2025淄博期末]将从1开始的自然数按以下规律排列成一个三角形数阵：
…
例如：第3行上的数“6”可记作(3,4),第5行上的数“19”可记作(5,7),则在这个数阵中的数“2024”可记作(A)A. (45,2)B. (44,3)C. (43,5)D. (43,7)

答案： A

5. 观察下列一系列数：
…

按照这种规律排下去,那么第8行从左边数第15个数是64。

答案： 64 【点拨】由题中数阵可得,每一行的最后一个数的绝对值是$n^{2}$,所以第8行从左边数第15个数的绝对值是$7^{2}+15=64$,因为图中的奇数都是负数,偶数都是正数,所以第8行从左边数第15个数是64.

6. 如图,用规格相同的小棒摆成一组图案,图案①需要4根小棒,图案②需要12根小棒,图案③需要20根小棒,…$$,按此规律摆下去,第$n$个图案需要小棒数是(D)


A.$4n$
B.$8n+4$
C.$6n-2$
D.$8n-4$

答案： D 【点拨】根据题意,得图案①需要$4=4×(2×1-1)$根小棒,图案②需要$12=4×(2×2-1)$根小棒,图案③需要$20=4×(2×3-1)$根小棒,…,由此发现,第n个图案需要小棒数是$4(2n-1)=8n-4.$

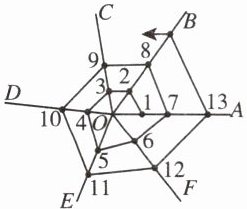
7. 如图,以$O为端点画射线OA, OB, OC, OD, OE, OF$,再从射线$OA$上某点开始按逆时针方向依次在射线上描点并连线,若将射线上所描的点依次记为1,2,3,4,5,6,…$$,那么第2025个点在射线OC上。
]

答案： OC 【点拨】因为1在射线OA上,2在射线OB上,3在射线OC上,4在射线OD上,5在射线OE上,6在射线OF上,7在射线OA上,…,所以每六个一循环.因为$2025÷6=337... 3$,所以所描的第2025个点所在的射线和第3个点所在的射线一样.所以第2025个点在射线OC上.