第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
15. [2025·聊城月考]如图,数轴上的$A$,$B$,$C三点所表示的数分别为a$,$b$,$c$。根据图中各点的位置,下列各式大于$0$的是(
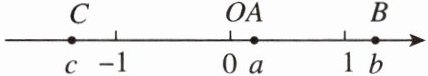
A.$(a - 1)(b - 1)$
B.$(b - 1)(c - 1)$
C.$(a + c)(a - b)$
D.$(b + 1)(c - 1)$
C
)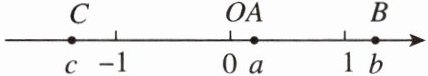
A.$(a - 1)(b - 1)$
B.$(b - 1)(c - 1)$
C.$(a + c)(a - b)$
D.$(b + 1)(c - 1)$
答案:
15.C [点拨]从数轴可知a-1<0,b-1>0,c-1<0,a+c<0,a-b<0,b+1>0,c+1<0,则(a-1)(b-1)<0,选项A不符合题意;(b-1)(c-1)<0,选项B不符合题意;(a+c)(a-b)>0,选项C符合题意;(b+1)(c-1)<0,选项D不符合题意.故选C.
16. 下列说法:①$0的倒数是0$;②如果$a + b < 0且ab < 0$,那么$a$,$b$异号且负数的绝对值较大;③如果$ab = 0$,那么$a$,$b中至少有一个为0$;④几个有理数相乘,积的符号由负因数的个数确定. 其中正确的有 (
②③
)。
答案:
16.②③
17. 新考法 分类讨论法 已知$a$,$b$互为相反数,$c$,$d$互为倒数,$n的绝对值为3$,则$\frac{a + b}{a + b + n} - 2cd + 3n$的值为
7或-11
。
答案:
17.7或-11 [点拨]因为a,b互为相反数,c,d互为倒数,n的绝对值为3,所以a+b=0,cd=1,n=±3.当n=3时,原式=0-2×1+3×3=-2+9=7;当n=-3时,原式=0-2×1+3×(-3)=-2-9=-11.综上,$\frac{a+b}{a+b+n}-2cd+3n$的值为7或-11.
18. 新视角 新定义题 定义一种新运算“$*$”,规定有理数$a\ast b = 4ab$,如$2\ast3 = 4×2×3 = 24$。
(1)求$5\ast( - 3)$的值;
(2)求$(-\frac{1}{6})\ast(\frac{3}{2}\ast5)$的值。
(1)求$5\ast( - 3)$的值;
(2)求$(-\frac{1}{6})\ast(\frac{3}{2}\ast5)$的值。
答案:
18.[解]
(1)5*(-3)=4×5×(-3)=-60.
(2)($-\frac{1}{6}$)*($\frac{3}{2}$*5)=($-\frac{1}{6}$)*(4×$\frac{3}{2}$×5)=($-\frac{1}{6}$)*30=4×($-\frac{1}{6}$)×30=-20.
(1)5*(-3)=4×5×(-3)=-60.
(2)($-\frac{1}{6}$)*($\frac{3}{2}$*5)=($-\frac{1}{6}$)*(4×$\frac{3}{2}$×5)=($-\frac{1}{6}$)*30=4×($-\frac{1}{6}$)×30=-20.
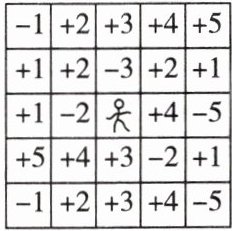
19. 情境题 游戏活动型 如图是一个“冲出围城”的游戏,规则如下:城中人(在最中间)想要冲出围城,可以横走也可以竖走,但不可以斜走,每走一格就可以得到格中相应的数作为生命值,每格中的数用乘法累计. 当生命值为正数且小于$ + 9$,并且人所在的格子处于最外圈时,就可以冲出围城,否则不可以出城.
例如:$( - 2)×( + 2)×( + 2)×( - 1) = + 8 < + 9$,所以$-2→+2→+2→-1$就是一条冲出围城的路线.
把你找到的冲出围城的路线用箭头在图中表示出来.(画出一条路线即可)
例如:$( - 2)×( + 2)×( + 2)×( - 1) = + 8 < + 9$,所以$-2→+2→+2→-1$就是一条冲出围城的路线.
把你找到的冲出围城的路线用箭头在图中表示出来.(画出一条路线即可)

答案:
19.[解]冲出围城的路线如图所示.(答案不唯一)
19.[解]冲出围城的路线如图所示.(答案不唯一)

20. 新考法 分类讨论法
【阅读】我们学习了有理数的加法法则与有理数的乘法法则. 在学习此内容时,掌握了法则,同时也学会了分类思考.
【探索】
(1)若$ab = 6$,则$a + b$的值为:①正数;②负数;③$0$. 你认为结果可能是
(2)若$a + b = - 5$,且$a$,$b$均为整数,则$ab$的最大值为
(3)数轴上$A$,$B两点分别表示有理数a$,$b$,若$ab < 0$,试比较$a + b与0$的大小.
【阅读】我们学习了有理数的加法法则与有理数的乘法法则. 在学习此内容时,掌握了法则,同时也学会了分类思考.
【探索】
(1)若$ab = 6$,则$a + b$的值为:①正数;②负数;③$0$. 你认为结果可能是
①②
;(填序号)(2)若$a + b = - 5$,且$a$,$b$均为整数,则$ab$的最大值为
6
;(3)数轴上$A$,$B两点分别表示有理数a$,$b$,若$ab < 0$,试比较$a + b与0$的大小.
因为ab<0,所以a,b异号.设a>0,则b<0,若|a|>|b|,则a+b>0,若|a|=|b|,则a+b=0,若|a|<|b|,则a+b<0;设a<0,则b>0,若|a|>|b|,则a+b<0,若|a|=|b|,则a+b=0,若|a|<|b|,则a+b>0.
答案:
20.[解]
(1)①②
(2)6
(3)因为ab<0,所以a,b异号.设a>0,则b<0,若|a|>|b|,则a+b>0,若|a|=|b|,则a+b=0,若|a|<|b|,则a+b<0;设a<0,则b>0,若|a|>|b|,则a+b<0,若|a|=|b|,则a+b=0,若|a|<|b|,则a+b>0.
(1)①②
(2)6
(3)因为ab<0,所以a,b异号.设a>0,则b<0,若|a|>|b|,则a+b>0,若|a|=|b|,则a+b=0,若|a|<|b|,则a+b<0;设a<0,则b>0,若|a|>|b|,则a+b<0,若|a|=|b|,则a+b=0,若|a|<|b|,则a+b>0.
查看更多完整答案,请扫码查看


