《2025年综合应用创新题典中点六年级数学上册鲁教版五四制》

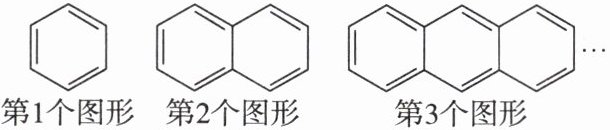
10. 新趋势 跨学科 苯是一种有机化合物,是组成结构最简单的芳香烃,可以合成一系列衍生物. 如图是某小组用小木棒摆放的苯及其衍生物的结构式,第1个图形需要9根小木棒,第2个图形需要16根小木棒,第3个图形需要23根小木棒,…,按此规律,第$n$个图形需要小木棒的根数为(7n+2)

A.$7n + 9$
B.$7n + 7$
C.$7n + 5$
D.$7n + 2$
]

答案： D 【点拨】因为第1个图形中小木棒的根数为9=7+2,第2个图形中小木棒的根数为16=7×2+2,第3个图形中小木棒的根数为23=7×3+2,…,所以第n个图形中小木棒的根数为7n+2.

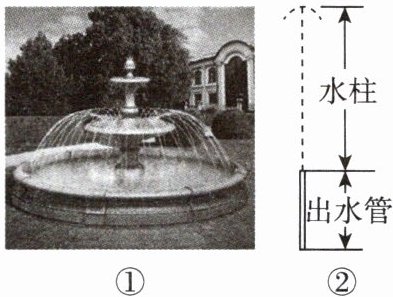
11. 新情境 生活应用 如图①,某中学新建了一个音乐喷泉,如图②,喷泉的水从出水管喷出形成漂亮的水柱,当出水量达到最大时,喷泉会响起优美的音乐,此时水柱的高度比出水管的高度的2倍还高$10cm$,设出水管的高度为$ncm$,当喷泉响起优美的音乐时,出水管和水柱的总高度为(n+2n+10)$cm$.
]

答案： (n+2n+10)

12. 在全国统一的鞋号中,成年男鞋共有14种尺码,其中最小的尺码是$23.5cm$,各相邻的两种尺码均相差$0.5cm$,如果从尺码最小的鞋开始标号,所对应的尺码(单位：$cm$)如下表所示：

(1)标号为7的鞋的尺码为多少？
(2)标号为$m(1\leqslant m\leqslant14$,且$m$为整数)的鞋的尺码如何表示？

答案： 【解】
(1)23.5+(7-1)×0.5=26.5(cm),即标号为7的鞋的尺码为26.5cm.
(2)标号为m(1≤m≤14,且m为整数)的鞋的尺码可表示为[23.5+0.5(m-1)]cm.

13. 体育老师到文体店买足球,足球的价格为$a$元/个,买10个以上(含10个)按总价的八折优惠.
(1)购买8个足球应付8a元,购买15个足球应付______12a元.
(2)购买$b$个足球应付多少钱？

答案： 【解】
(1)8a;12a
(2)当b＜10时,应付的钱数为ab元;当b≥10时,应付的钱数为0.8ab元.

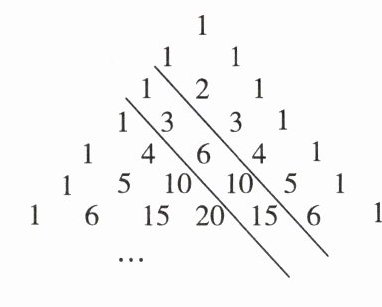
14. 新考向 数学文化 如图被称为“杨辉三角”或“贾宪三角”. 其规律是：从第三行起,每行两端的数都是1,其余各数都等于该数“两肩”上的数之和. 图中两直线之间的一列数：1,3,6,10,15,…,我们把第一个数记为$a_1$,第二个数记为$a_2$,第三个数记为$a_3$,…,第$n个数记为a_n$.
(1)表示出$a_n$；
(2)求$a_4 + a_{200}$的值.
]

答案： 【解】
(1)观察可知第n个数$a_{n}=1+2+\cdots +n=\frac{1}{2}n(n+1)$.
(2)$a_{4}+a_{200}=\frac{1}{2}× 4× (4+1)+\frac{1}{2}× 200× (200+1)=$20110.