《2025年综合应用创新题典中点六年级数学上册鲁教版五四制》

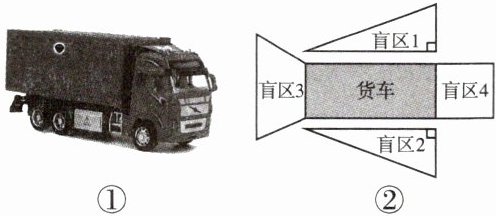
10. 据调查,很多交通事故和汽车盲区有关,汽车盲区是指驾驶员位于正常驾驶位置时,其视线被车体遮挡而不能直接观察到的那部分区域.在汽车行驶时,若行人、非机动车处于汽车盲区内,极易引发交通事故.在一次普及“交通安全知识”的综合实践活动中,七年级学生们对货车(如图①)的盲区面积进行探究,得到货车盲区的部分分布图(如图②),盲区1,2的面积相同,都是$\frac{3}{2}ab + a^{2}$,盲区3的面积是$-2ab + 4a^{2}$,盲区4的面积是$a^{2}$.
(1)用含a,b的代数式表示图中盲区的总面积(结果需化简).
(2)若$a = 2$,$b = 2$,求图中盲区的总面积.

答案： 【解】（1）由题意，得盲区的总面积=2（$\frac{3}{2}$ab+a²）+（-2ab+4a²）+a²=3ab+2a²-2ab+4a²+a²=7a²+ab.
（2）当a=2，b=2时，7a²+ab=7×2²+2×2=32，所以图中盲区的总面积为32.

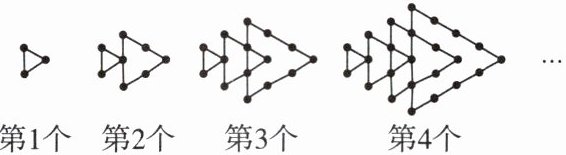
11. 如图,将形状、大小完全相同的“·”按照一定规律摆放,第1个图案中“·”的个数是3,第2个图案中“·”的个数是8,第3个图案中“·”的个数是15,…,以此类推,则第n(n是正整数)个图案中“·”的个数是(A)


A.$n^{2}+2n$
B.$n^{2}+n$
C.$n^{2}-n$
D.$n^{2}-2n$

答案： A 【点拨】第1个图案中“·”的个数为3=1²+2×1，第2个图案中“·”的个数为8=2²+2×2，第3个图案中“·”的个数为15=3²+2×3，第4个图案中“·”的个数为24=4²+2×4，…，第n个图案中“·”的个数为n²+2n.故选A.

12. 已知$a + b = 4$,$ab = - 2$,求$(5a - 4b - 4ab) - 3(a - 2b - ab)$的值.

答案： 【解】原式=5a-4b-4ab-3a+6b+3ab=2（a+b）-ab，
当a+b=4，ab=-2时，
原式=2（a+b）-ab=2×4-（-2）=10.

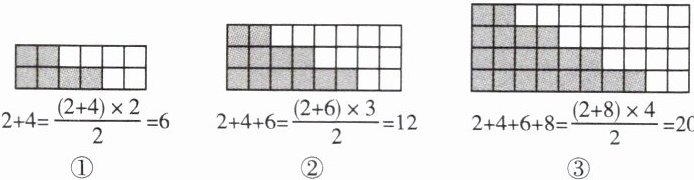
13. 数形结合思想是一种重要的数学思想方法.数形结合就是把抽象的数学语言与直观的图形结合起来,通过“以形助数”或“以数解形”使复杂问题简单化、抽象问题具体化,从而实现优化解题途径的目的.在数学活动中,老师提出一个数学问题：计算$2 + 4 + 6 + 8 + … + 2n$(n为正整数).奋进小组进行了如下分析：如图②,可以把求$2 + 4 + 6$的和转化为求阴影方格的个数,他们把方格的个数扩大一倍拼成一个大长方形,而大长方形中小方格数的一半就是阴影方格的个数.根据上述探究过程得到老师提出问题的结果为n²+n.

答案： n²+n