《2025年综合应用创新题典中点六年级数学上册鲁教版五四制》

8. 母题教材P132习题T2小颖和小亮在玩一个数字游戏.小颖对小亮说：“小亮,你在心里想好一个数,按照下列步骤进行运算,把这个数乘2,然后减4,再把所得的数乘3,然后再加20,把你的结果告诉我,我就知道你心里想的数了.”小亮试了几次,小颖都猜对了,你知道这是为什么吗？

答案： 【解】设小亮心里想好的数为x，那么把这个数乘2是2x，然后减4是2x-4，再把所得的数乘3是3(2x-4)，然后再加20是3(2x-4)+20=6x-12+20=6x+8，因此小颖只要把结果减8后再除以6就可以得到小亮心里想好的数.

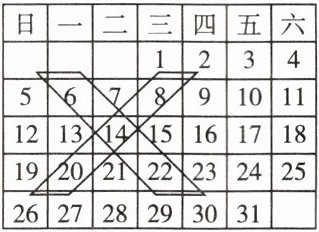
9. 母题·教材P131习题T1日历是一份来自时间的礼物,它让生活有迹可循,同时提醒我们要珍惜时间,不负韶华.如图是2025年1月份的日历,小颖用一个“X”形框选中了5个数.
(1)请通过计算说明图中“X”形框选中的五个数的和与中间数的关系；
(2)若在日历中任意画一个这样的“X”形框且选中5个数,(1)中的关系是否仍然成立？请说明理由.
]

答案： 【解】
(1)因为6+8+14+20+22=70=5×14，所以图中“X”形框选中的五个数的和是中间数的5倍.
(2)成立. 理由如下：设“X”形框选中的五个数中，中间的数为x，则其余四个数分别为x-6，x-8，x+6，x+8，所以这五个数的和为(x-6)+(x-8)+(x+6)+(x+8)+x=5x，所以
(1)中的关系仍然成立.

10. 新趋势·跨学科“柳庭风静人眠昼,昼眠人静风庭柳”,从左向右读与从右向左读完全相同,这样的诗称为回文诗.在数学中也有这样的一类数.一个自然数从左向右读与从右向左读完全相等,这样的数称为回文数,如121与1221均为回文数.回文数与其各个数位上的数字之和的差值称为回自差,如121的回自差为$121-(1 + 2 + 1)= 117$.
(1)请你直接写出最小的三位回文数,并求其回自差；
(2)任意三位回文数的回自差最大能被哪个正整数整除？请你说明理由；
(3)任意四位回文数的回自差最大能被哪个正整数整除？请你说明理由.
]

答案： 【解】
(1)由题意得，最小的三位回文数为101，所以最小的三位回文数的回自差为101-(1+0+1)=99.
(2)任意三位回文数的回自差最大能被9整除，理由如下：设一个三位回文数为$\overline{aba}$(a≠0)，其中a，b都为不超过9的自然数，则该三位回文数为100a+10b+a=101a+10b，所以该三位回文数的回自差为101a+10b-(a+b+a)=99a+9b=9(11a+b). 因为a，b都是整数，所以11a+b也是整数，所以该三位回文数的回自差一定是9的倍数，所以任意三位回文数的回自差最大能被9整除.
(3)设该四位回文数的千位数字为x，百位数字为y，则该四位回文数为1000x+100y+10y+x=1001x+110y，所以该四位回文数的回自差为1001x+110y-(x+y+y+x)=999x+108y=27(37x+4y). 因为x，y都是整数，所以37x+4y是整数，所以该四位回文数的回自差一定是27的倍数，所以任意四位回文数的回自差最大能被27整除.