《2025年综合应用创新题典中点六年级数学上册鲁教版五四制》

1. 已知多项式$A = x^{2}+2y^{2}-z^{2}$,$B= -4x^{2}+3y^{2}+2z^{2}$,且$A + B + C = 0$,则$C$为(B)
A.$5x^{2}-y^{2}-z^{2}$
B.$3x^{2}-5y^{2}-z^{2}$
C.$3x^{2}-y^{2}-3z^{2}$
D.$3x^{2}-5y^{2}+z^{2}$

答案： B

2. 下面是小芳做的一道多项式的加减运算题,但她不小心把一滴墨水滴在了上面：$(-x^{2}+3xy-\frac{1}{2}y^{2})-2(-\frac{5}{2}x^{2}+4xy-\frac{3}{2}y^{2})= $ $-5xy+\frac{5}{2}y^{2}$,阴影部分即为被墨水弄污的部分。那么被墨水遮住的一项应是(D)
A.$4x^{2}-5y$
B.$2y - x$
C.$5x$
D.$4x^{2}$

答案： D

3. [2025·德州期末]已知$x - 3y = 4$,那么代数式$x - 3y - 3(y - x)-2(x - 3)$的值为(C)
A.12
B.13
C.14
D.16

答案： C [点拨]原式=x - 3y - 3y + 3x - 2x + 6 = 2x - 6y + 6.因为x - 3y = 4,所以原式=2(x - 3y) + 6 = 2×4 + 6 = 8 + 6 = 14.

4. [母题教材P125习题T2]先化简,再求值：$(2m^{2}+3n^{2}-mn)-2(3m^{2}+\frac{11}{2}n^{2}-\frac{1}{2}mn)$,其中$m^{2}+2n^{2}= 6$。

答案： [解]原式=2m²+3n² - mn - 6m² - 11n²+mn = - 4m² - 8n² = - 4(m²+2n²).当m²+2n² = 6时,原式= - 4×6 = - 24.

5. [2025·烟台期末]一根铁丝正好可以围成一个长是$2a + b$,宽是$a + 3b$的长方形框,现剪去一段铁丝,若剪去的铁丝正好可以围成一个长是$a$,宽是$2b$的长方形(均不计接缝),则剩下的铁丝长是(A)
A.$4a + 4b$
B.$2a + 2b$
C.$4a + 2b$
D.$5a + 6b$

答案： A

6. [新情境生活应用]某果园引入了$m$个采摘机器人,这些机器人被分为两组,每组的工作效率不同。第一组有$n$个机器人,每个机器人平均8秒采摘一个苹果；第二组包含剩余的机器人,每个机器人平均6秒采摘一个苹果。同时,果园内还有10名熟练的采摘工人,他们每个人平均5秒采摘一个苹果。机器人与工人同时工作1小时,则这$m$个机器人比这10名工人多采摘的苹果个数是(B)
A.$120(m - 2n)-720$
B.$600m - 150n - 7200$
C.$600m + 450n - 7200$
D.$120m - 150n - 720$

答案： B

7. [2025·淄博期末]若多项式$2x^{3}-6x^{2}+x - 1与多项式3x^{3}+2mx^{2}-5x + 3$的差不含二次项,则$m$等于(D)
A.2
B.$-2$
C.3
D.$-3$

答案： D [点拨]2x³ - 6x²+x - 1 - (3x³+2mx² - 5x + 3)=2x³ - 6x²+x - 1 - 3x³ - 2mx²+5x - 3 = - x³+( - 6 - 2m)x²+6x - 4.因为多项式2x³ - 6x²+x - 1与多项式3x³+2mx² - 5x + 3的差不含二次项，所以 - 6 - 2m = 0,解得m = - 3.故选D.

8. 已知$x^{2}-2x - 5 = 0$,当$y = 1$时,$ay^{3}+4by + 3$的值等于4,则当$y = -1$时,$-2(x + 2by)+(x^{2}-ay^{3})$的值等于(6)
A.1
B.9
C.4
D.6

答案： D [点拨]当y = 1时,ay³+4by + 3 = a + 4b + 3 = 4,所以a + 4b = 1.因为x² - 2x - 5 = 0,所以x² - 2x = 5.所以当y = - 1时, - 2(x + 2by)+(x² - ay³)= - 2x - 4by + x² - ay³ = - 2x + 4b + x²+a = - 2x + x²+a + 4b = 5 + 1 = 6.

9. 把边长为$6a$的正方形纸片按图①中的虚线剪开,无缝隙且不重叠地拼接成图②的长方形。则长方形的周长与正方形的周长比较( )


A.不变
B.减少$2a$
C.增加$2a$
D.增加$4a$

答案：
C [点拨]由于是无缝隙且不重叠地拼接成，故各边长如图所示: 正方形的周长为4×6a = 24a，长方形的周长为(3a + 6a + 4a)×2 = 26a,故长方形的周长比正方形的周长增加了2a，故选C.

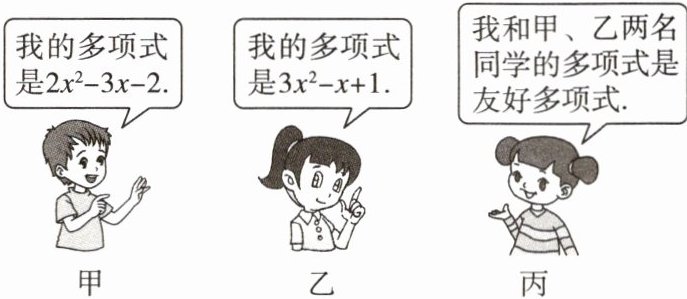
10. [新视角结论开放题]数学课上,老师设计了一个数学游戏：若两个多项式相减的结果等于第三个多项式,则称这三个多项式为“友好多项式”。甲、乙、丙三名同学各有一张多项式卡片,下面是甲、乙、丙三名同学的对话,根据对话内容,可以知道丙的多项式可以是- x² - 2x - 3(写出一个即可)。

答案： - x² - 2x - 3(答案不唯一)