《2025年综合应用创新题典中点六年级数学上册鲁教版五四制》

1. 计算$2a+3a$的结果正确的是(A)
A.$5a$
B.$6a$
C.$5a^{2}$
D.$6a^{2}$

答案： A

2. 下列式子中,不相等的一组是(C)
A.$2a与a+a$
B.$a+2与2+a$
C.$a-2与2-a$
D.$2(a+b)与2a+2b$

答案： C

3. 已知$2x^{6}y^{2}和-\frac{1}{3}x^{3m}y^{n}$是同类项,则$9m^{2}-5mn-17$的值是(A)
A.$-1$
B.$-2$
C.$-3$
D.$-4$

答案： A

4. 下列式子中,去括号正确的是(A)
A.$-3a+(-a^{2}+3ab)= -3a-a^{2}+3ab$
B.$13ab-(a^{2}-4ab-5b^{2})= 13ab-a^{2}-4ab-5b^{2}$
C.$-3(a+b-c+1)= -3a-3b+3c+1$
D.$9y^{2}-(3xy^{2}-5y^{2}+4)= 9y^{2}-3xy^{2}+5y^{2}+4$

答案： A

5. 新考法作差法若$M= 3x^{2}-2x+1, N= 4x^{2}-2x+5$,则$M与N$的大小关系是(A)
A.$M＜N$
B.$M＞N$
C.$M= N$
D.无法确定

答案： A

6. 新情境生活应用某校组织若干名师生进行社会实践活动。若学校只租用45座的客车$x$辆,则余下15人无座位；若只租用60座的客车,则可少租用1辆,且最后一辆还没坐满,那么乘坐最后一辆60座客车的人数是(B)
A.$75-15x$
B.$135-15x$
C.$75+15x$
D.$135-60x$

答案： B 【点拨】总人数为$(45x+15)$人,则乘坐最后一辆60座客车的人数为$45x+15-60(x-2)=135-15x.$

7. 若$A与B$都是二次多项式,则$A - B$：(1)一定是二次式；(2)可能是四次式；(3)可能是一次式；(4)可能是非零常数；(5)不可能是零。上述结论中,不正确的有(C)
A.5个
B.4个
C.3个
D.2个

答案： C 【点拨】因为多项式相减,也就是合并同类项,而合并同类项时只是把系数相减,字母和字母的指数不变,所以结果的次数一定不高于二次,当二次项相同时,合并后不含二次项,当$A=B$时,合并后结果为0,所以
(1)
(2)
(5)是错误的.

8. [2025·泰安月考]如图①,小长方形纸片的长为2,宽为1,将4张这样的小长方形纸片按图②所示的方式不重叠的放在大长方形内,未被覆盖的部分(阴影部分)恰好被分割为长方形Ⅰ和Ⅱ,设长方形Ⅰ和Ⅱ的周长分别为$C_{1}和C_{2}$,则$C_{1}与C_{2}$的大小关系为(A)

A.$C_{1}= C_{2}$
B.$C_{1}＞C_{2}$
C.$C_{1}＜C_{2}$

D.无法判断

答案： A 【点拨】设大长方形的长为a,则长方形Ⅰ的长为$(a-1)$,宽为2,长方形Ⅱ的长为$(a-2)$,宽为3,所以$C_{1}=2(a-1+2)=2a+2,C_{2}=2(a-2+3)=2a+2$.所以$C_{1}=C_{2}.$

9. [2025·烟台模拟]已知$-2x^{2}y^{n}+3x^{m}y= x^{2}y$,则$m+n= $3。

答案： 3

10. 新考法整体思想已知$a+b= -3, c-d= 4$,则$(b+c)-(d-a)$的值是1。

答案： 1

11. 若关于$x,y的多项式x^{2}+axy-(bx^{2}-y-3)$不含二次项,则$a - b$的值为-1。

答案： -1 【点拨】$x^{2}+axy-(bx^{2}-y-3)=x^{2}+axy-bx^{2}+y+3=(1-b)x^{2}+axy+y+3$.由题意,知$1-b=0$且$a=0$,所以$b=1$.所以$a-b=0-1=-1.$

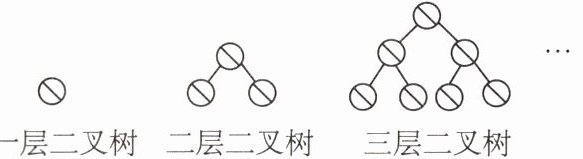
12. 新考法跨学科在计算机程序中,二叉树是一种表示数据结构的方法,如图,一层二叉树的结点总数为1,二层二叉树的结点总数为3,三层二叉树的结点总数为7,…$$,照此规律,$n$层二叉树的结点总数为$2^{n}-1$。
]

答案： $2^{n}-1$ 【点拨】由所给图形可知,一层二叉树的结点总数为:$1=2^{1}-1$;二层二叉树的结点总数为:$3=2^{2}-1$;三层二叉树的结点总数为:$7=2^{3}-1$;…;所以n层二叉树的结点总数为$2^{n}-1.$

13. (12分)化简：
(1)$5(mn-2m)+3(4m-2mn)$；
(2)$-3(x+2y-1)-\frac{1}{2}(-6y-4x+2)$。

答案： 【解】
(1)$5(mn-2m)+3(4m-2mn)$$=5mn-10m+12m-6mn$$=-mn+2m.$
(2)$-3(x+2y-1)-\frac{1}{2}(-6y-4x+2)$$=-3x-6y+3+3y+2x-1$$=-x-3y+2.$