《2025年综合应用创新题典中点六年级数学上册鲁教版五四制》

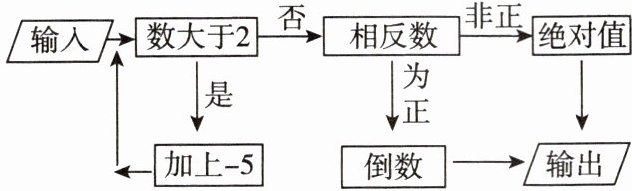
11. 如图是一个“有理数转换器”,当输入的数为 $8$ 时,则输出的数为(B)


A.$-\dfrac{1}{2}$
B.$\dfrac{1}{2}$
C.$-2$
D.$2$

答案： B　[点拨]当输入8时，因为8＞2,所以8+(−5)=3＞2,所以3+(−5)=−2＜2,所以−2 的相反数为2＞0,所以2的倒数为$\frac{1}{2}$,所以当输入的数是8时，输出的数为$\frac{1}{2}$.

12. 小华探究“幻方”时,提出了一个问题：如图,将 $0$,$-2$,$-1$,$1$,$2$ 这五个数分别填在五个小正方形内,使横向三个数之和与纵向三个数之和相等,则填入中间位置的小正方形内的数可以是 。(写出一个符合题意的数即可)

答案：
0(答案不唯一)　　[点拨]由题意，填写如下:
　　　　　　　
1+0+(−1)=0,2+0+(−2)=0,满足题意.故答案可为0.

13. 用 $[x]$ 表示不超过 $x$ 的整数中最大的整数,如 $[2.23]= 2$,$[-3.24]= -4$。请计算：
(1) $[3.5]+[-3]$；
(2) $[-7.25]+[-\dfrac{1}{3}]$。

答案： [解]
(1)[3.5]+[-3]=3+(−3)=0.
(2)$[-7.25]+[-\frac {1}{3}]=(-8)+(-1)=-9.$

14. (1) 用“$＞$”“$＜$”或“$=$”填空：
$|(+4)+(+7)|$ =$|+4|+|+7|$；
$|(-4)+(-7)|$ =$|-4|+|-7|$；
$|(+4)+(-7)|$ ＜$|+4|+|-7|$；
$|(-4)+(+7)|$ ＜$|-4|+|+7|$；
$|0+(-7)|$ =$|0|+|-7|$。
(2) 做完上述填空题,你可以得出什么结论？请用字母表述你的结论。
①当a,b同号时,|a+b|=|a|+|b|;②当a,b异号时,|a+b|＜|a|+|b|;③当a,b中至少有一个是0时,|a+b|=|a|+|b|.

答案： [解]
(1)=;=;＜;＜;=
(2)①当a,b同号时,|a+b|=|a|+|b|;
　②当a,b异号时,|a+b|＜|a|+|b|;
　③当a,b中至少有一个是0时,|a+b|=|a|+|b|.

15. 在某次抗洪抢险中,解放军战士的冲锋舟沿东西方向的河流抢救灾民,早晨从甲村出发,晚上到达乙村,约定向东为正方向,当天的航行路程记录如下(单位：$km$)：
$+14$,$-10$,$+8$,$-7$,$+13$,$-6$,$+12$,$-6$。
(1) 请确定乙村相对于甲村的具体方位。
(2) 救灾过程中,冲锋舟离出发地最远有多远？
(3) 为了尽快抢救灾民,冲锋舟出发前就加满了油,而且在救灾过程中不再加油,若冲锋舟每千米耗油 $0.5$ 升,那么该冲锋舟油箱容量至少是多少升？

答案： [解]
(1)因为(+14)+(−10)+(+8)+(−7)+(+13)+(−6)+(+12)+(−6)=14−10+8−7+13−6+12−6=18(km),所以乙村位于甲村的正东方向，距离甲村18km.
(2)第1次记录时冲锋舟离出发地の距离为|+14|=14(km);
　第2次记录时冲锋舟离出发地の距离为|14+(−10)|=4(km);
　第3次记录时冲锋舟离出发地の距离为|4+(+8)|=12(km);
　第4次记录时冲锋舟离出发地の距离为|12+(−7)|=5(km);
　第5次记录时冲锋舟离出发地の距离为|5+(+13)|=18(km);
　第6次记录时冲锋舟离出发地の距离为|18+(−6)|=12(km);
　第7次记录时冲锋舟离出发地の距离为|12+(+12)|=24(km);
　第8次记录时冲锋舟离出发地の距离为|24+(−6)|=18(km).
　由此可知，救灾过程中，冲锋舟离出发地最远有24km.
(3)冲锋舟当天航行总路程为|+14|+|−10|+|+8|+|−7|+|+13|+|−6|+|+12|+|−6|=14+10+8+7+13+6+12+6=76(km),76×0.5=38(升),所以该冲锋舟油箱容量至少是38升.

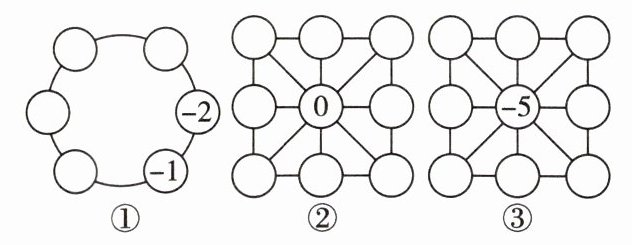
16. (1) 请在图①的各圆圈内填上适当的数,使每个圆圈内的数都等于与它相邻的两个数的和。
(2) 如图②,在各圆圈内填上适当的数,使每条线上的 $3$ 个数的和为 $0$。
(3) 如图③,将图②中心处的 $0$ 改为 $-5$,那么怎样填写才能使每条线上的 $3$ 个数的和为 $-15$？

答案：
[解]
(1)如图①.
(2)如图②.(答案不唯一)
(3)如图③.(答案不唯一)