《2025年点拨训练八年级数学上册沪科版安徽专版》

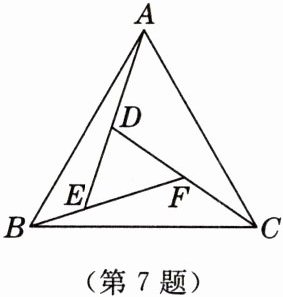
7. 如图,$\triangle ABC$是等边三角形,点$D$,$E$,$F在\triangle ABC$的内部,点$D在AE$上,点$E在BF$上,点$F在CD$上,且$\angle BAE:\angle CBF:\angle ACD= 1:2:3$,则$\triangle DEF$的形状是(A)

A.等腰三角形
B.等边三角形
C.直角三角形
D.等腰直角三角形

答案： A

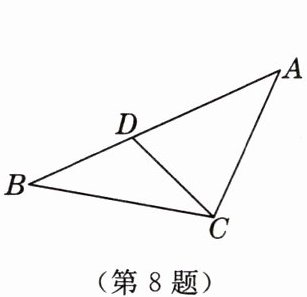
8. 如图,在$\triangle ABC$中,点$D在边AB$上,且$\angle ADC= \angle ACD= 2\angle B$,若$AB= 27$,$\triangle ADC的周长为43$,则$CD= $11.

答案： 11

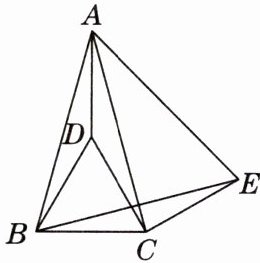
9. 如图,在$\triangle ABC$中,$AB= AC$,点$D在\triangle ABC$内,$BD= BC$,$\angle DBC= 60^{\circ}$,点$E在\triangle ABC$外,$\angle BCE= 150^{\circ}$,$\angle ABE= 60^{\circ}$.求证：$\triangle ABE$是等边三角形.

答案： 证明：
∵BD=BC,∠DBC=60°,
∴△DBC是等边三角形,∠BDC=$\frac{1}{2}$×(180°-60°)=60°,
∴DB=DC.
在△ADB和△ADC中,$\left\{\begin{array}{l} AB=AC,\\ AD=AD,\\ DB=DC,\end{array}\right. $
∴△ADB≌△ADC(SSS),
∴∠ADB=∠ADC=$\frac{1}{2}$(360°-∠BDC)=150°.
∵∠ABE=∠DBC=60°,
∴∠ABD=∠EBC.
在△ABD和△EBC中,$\left\{\begin{array}{l} ∠ABD=∠EBC,\\ BD=BC,\\ ∠ADB=∠ECB=150°, \end{array}\right. $
∴△ABD≌△EBC(ASA),
∴AB=EB.
又
∵∠ABE=60°,
∴△ABE是等边三角形.

如图,在$\triangle ABC$中,$\angle ABC$,$\angle ACB的平分线相交于点O$,过点$O作EF// BC分别交AB$,$AC于点E$,$F$.

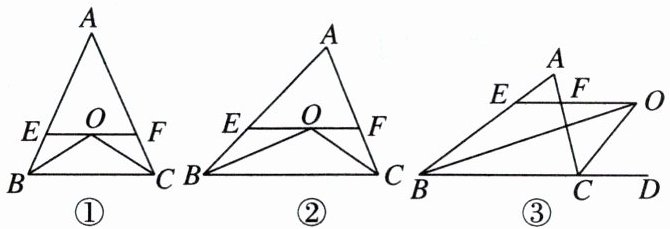
(1)【识别等腰】如图①,若$AB= AC$,图中有5个等腰三角形,且$EF与BE$,$CF$间的数量关系是EF=BE+CF=2BE=2CF.
(2)【探索建模】如图②,若$AB\neq AC$,其他条件不变,(1)问中$EF与BE$,$CF$间的数量关系还成立吗？请说明理由.
EF与BE,CF间的数量关系EF=BE+CF成立，EF=2BE=2CF不成立.理由略.
(3)【模型应用】在(2)的条件下,若$AB= 10$,$AC= 15$,则$\triangle AEF$的周长为25.
(4)【变式探究】如图③,在$\triangle ABC$中,若$AB\neq AC$,$\angle ABC的平分线与三角形外角\angle ACD的平分线CO交于点O$,过点$O作OE// BC交AB于点E$,交$AC于点F$,则$EF与BE$,$CF$间的数量关系为EF=BE-CF.

答案：
(1)5;EF=BE+CF=2BE=2CF
(2)EF与BE,CF间的数量关系EF=BE+CF成立，
EF=2BE=2CF不成立.理由略.
(3)25
(4)EF=BE-CF