《2025年点拨训练八年级数学上册沪科版安徽专版》

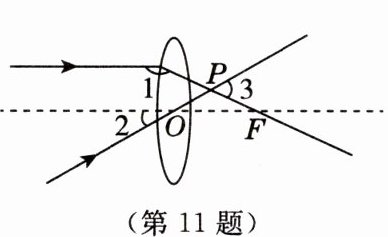
11. 跨学科·物理 [2024·六安模拟改编]如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心$O的光线相交于点P$,若$\angle 1= 155^{\circ}$,$\angle 3= 55^{\circ}$,则$\angle 2$的度数为(B)

A.$25^{\circ}$
B.$30^{\circ}$
C.$35^{\circ}$
D.$40^{\circ}$

答案： 解：设平行于主光轴的光线与凸透镜上交点为A，经过光心O的光线与凸透镜下交点为B，折射光线为AP。
因为入射光线平行于主光轴，所以∠1的邻补角为180° - 155° = 25°，该角与∠2的对顶角所在三角形的一个内角相等（两直线平行，同位角相等）。
在三角形OPF中，∠3是外角，等于不相邻的两个内角之和，其中一个内角为25°，所以∠2 = ∠3 - 25° = 55° - 25° = 30°。
答案：B

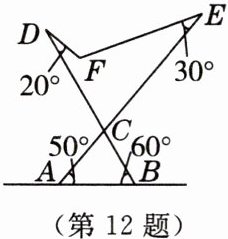
12. 真实情境 [2025年1月淮北期末]如图是可调躺椅示意图,$AE与BD的交点为C$,且$\angle CAB$、$\angle CBA$、$\angle D$的大小保持不变. 为了舒适,需调整$\angle E$的大小,使$\angle EFD= 130^{\circ}$,则图中$\angle E$应(A)

A.增加$10^{\circ}$
B.减少$10^{\circ}$
C.增加$20^{\circ}$
D.减少$20^{\circ}$

答案： A

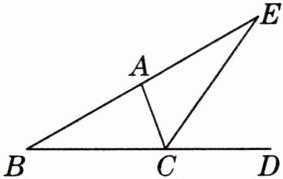
13. [2025·无锡模拟]如图,$CE是\triangle ABC的外角\angle ACD$的平分线,且$CE交BA的延长线于点E$.
(1) 若$\angle E= 25^{\circ}$,$\angle BAC= 80^{\circ}$,求$\angle B$的度数；
(2) 试说明：$\angle BAC= \angle B+2\angle E$.

答案： 【解析】：本题主要考查三角形的外角性质以及角平分线的性质。
（1）根据三角形外角性质，三角形的外角大于任何一个与它不相邻的内角，
所以$\angle ECD$是$\bigtriangleup BCE$的外角，
则$\angle ECD = \angle B + \angle E$。
已知$\angle E = 25^{\circ}$，
又因为$CE$是$\angle ACD$的平分线，
所以$\angle ACD = 2\angle ECD$。
再根据三角形外角性质，$\angle ACD$是$\bigtriangleup ABC$的外角，
所以$\angle ACD = \angle B + \angle BAC$。
将$\angle ACD = 2\angle ECD$和$\angle ECD = \angle B + \angle E$代入$\angle ACD = \angle B + \angle BAC$中，
得到$2(\angle B + \angle E) = \angle B + \angle BAC$。
已知$\angle BAC = 80^{\circ}$，$\angle E = 25^{\circ}$，
代入上式可得：
$2(\angle B + 25^{\circ}) = \angle B + 80^{\circ}$
$2\angle B + 50^{\circ} = \angle B + 80^{\circ}$
$\angle B = 30^{\circ}$
（2）证明：
因为$CE$平分$\angle ACD$，
所以$\angle ACD = 2\angle ECD$。
而$\angle ECD = \angle B + \angle E$，
所以$\angle ACD = 2(\angle B + \angle E)$。
又因为$\angle BAC = \angle ACD - \angle B$，
将$\angle ACD = 2(\angle B + \angle E)$代入$\angle BAC = \angle ACD - \angle B$中，
得到$\angle BAC = 2(\angle B + \angle E) - \angle B$。
化简后可得$\angle BAC = \angle B + 2\angle E$。
【答案】：
(1) $\angle B = 30^{\circ}$；
(2) 证明过程如上。

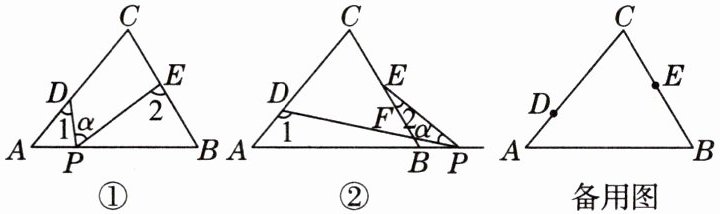
14. 中考趋势·探究建模 [2025年1月滁州期末]在$\triangle ABC$中,$\angle C= 70^{\circ}$,点$D$,$E分别是\triangle ABC边AC$,$BC$上的两个定点,$P$是平面内一动点.
【问题初探】
(1) 如图①,若点$P在线段AB$上运动,
①当$\angle \alpha=60^{\circ}$时,$\angle 1+\angle 2= $130°；
②$\angle \alpha$,$\angle 1$,$\angle 2$之间的数量关系为∠1+∠2=∠α+70°.
【深入探究】
(2) 若点$P运动到边AB$的延长线上,$PD交BC于点F$,如图②,则$\angle \alpha$,$\angle 1$,$\angle 2$之间有何关系？并说明理由.
∠1=∠α+∠2+70°
证明：
∵∠CFD是△EFP的外角
∴∠CFD=∠α+∠2
∵∠CFD是△CDF的外角
∴∠CFD=∠1+∠C
∴∠α+∠2=∠1+∠C
∵∠C=70°
∴∠1=∠α+∠2+70°
【拓展应用】
(3) 当点$P在\triangle ABC$的内部,且点$D$,$P$,$E$不共线时,记$\angle ADP= \angle 1$,$\angle BEP= \angle 2$,$\angle DPE= \angle \alpha$,试探究$\angle \alpha$,$\angle 1$,$\angle 2$之间的关系.
∠α=∠1+∠2+70°
证明：延长DP交BC于点F
∵∠EFP是△CDF的外角
∴∠EFP=∠1+∠C
∵∠α是△EFP的外角
∴∠α=∠2+∠EFP
∴∠α=∠2+∠1+∠C
∵∠C=70°
∴∠α=∠1+∠2+70°

答案：
(1)①130°
②∠1+∠2=∠α+70°
(2)∠1=∠α+∠2+70°
证明：
∵∠CFD是△EFP的外角
∴∠CFD=∠α+∠2
∵∠CFD是△CDF的外角
∴∠CFD=∠1+∠C
∴∠α+∠2=∠1+∠C
∵∠C=70°
∴∠1=∠α+∠2+70°
(3)∠α=∠1+∠2+70°
证明：延长DP交BC于点F
∵∠EFP是△CDF的外角
∴∠EFP=∠1+∠C
∵∠α是△EFP的外角
∴∠α=∠2+∠EFP
∴∠α=∠2+∠1+∠C
∵∠C=70°
∴∠α=∠1+∠2+70°