第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
两边及其
1星题 基础题
知识点1 判定三角形全等的基本事实:“边角边”
夹角
分别相等的两个三角形全等. 简记为“边角边”或“SAS”.1星题 基础题
知识点1 判定三角形全等的基本事实:“边角边”
答案:
夹角
1. 如图,已知$∠1= ∠2$,用“SAS”判定$△ABC\cong △ABD$,还需要的条件是(
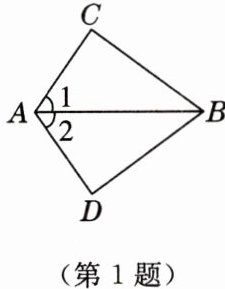
A.$BC= BD$
B.$AC= AD$
C.$∠C= ∠D$
D.$∠ABC= ∠ABD$
B
)
A.$BC= BD$
B.$AC= AD$
C.$∠C= ∠D$
D.$∠ABC= ∠ABD$
答案:
B
2. 在$△ABC和△DEF$中,下列给出的条件,能用“SAS”判定这两个三角形全等的是(
A.$AB= DE,BC= DF,∠A= ∠D$
B.$AB= EF,AC= DF,∠A= ∠D$
C.$AB= BC,DE= EF,∠B= ∠E$
D.$BC= EF,AC= DF,∠C= ∠F$
D
)A.$AB= DE,BC= DF,∠A= ∠D$
B.$AB= EF,AC= DF,∠A= ∠D$
C.$AB= BC,DE= EF,∠B= ∠E$
D.$BC= EF,AC= DF,∠C= ∠F$
答案:
D
3. [2025年1月湛江期末]如图,D,E分别在AB,AC上,若$AB= AC,AD= AE,∠A= 60^{\circ },∠B= 35^{\circ }$,则$∠BDC$的度数是
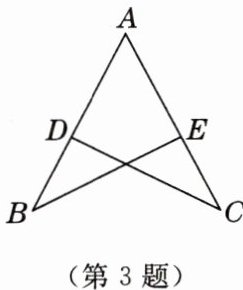
95°
.
答案:
95°
4. [2025年1月厦门期末]如图,小阳同学为电力公司设计了一个安全用电的标识,点A,D,C,F在同一条直线上,且$AF= DC,BC= EF,BC// EF$. 求证:$AB= DE$.
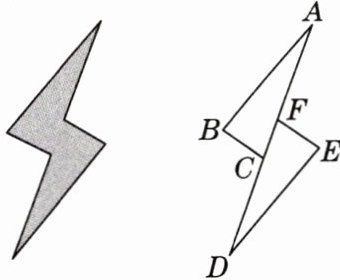

答案:
证明:
∵BC//EF,
∴∠ACB=∠DFE.
∵AF=CD,
∴AF+FC=CD+FC,即AC=DF又
∵BC=EF,
∴△ABC≌△DEF,
∴AB=DE.
∵BC//EF,
∴∠ACB=∠DFE.
∵AF=CD,
∴AF+FC=CD+FC,即AC=DF又
∵BC=EF,
∴△ABC≌△DEF,
∴AB=DE.
5. [2025年1月合肥期末]如图,$AB= AC,AD= AE,∠BAC= ∠DAE$,求证:$△ABD\cong △ACE$.
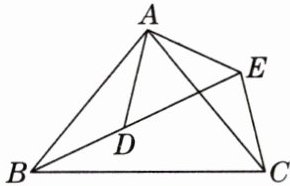

答案:
证明:
∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE,在△ABD和△ACE中,$\left\{\begin{array}{l} AB=AC,\\ ∠BAD=∠CAE,\\ AD=AE,\end{array}\right. $
∴△ABD≌△ACE(SAS).$\triangle ABD\cong \triangle ACE(SAS).$
∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE,在△ABD和△ACE中,$\left\{\begin{array}{l} AB=AC,\\ ∠BAD=∠CAE,\\ AD=AE,\end{array}\right. $
∴△ABD≌△ACE(SAS).$\triangle ABD\cong \triangle ACE(SAS).$
6. 跨学科·生物 在生物实验课上,老师布置了“测量锥形瓶内部底面内径”的任务. 小亮同学想到了以下这个方案:如图,用螺丝钉将两根小棒AD,BC的中点O固定,其中$AD= BC= 10cm,CD= 4cm$,则A,B间的距离为(

A.3 cm
B.4 cm
C.5 cm
D.6 cm
4cm
)
A.3 cm
B.4 cm
C.5 cm
D.6 cm
答案:
【解析】:本题可根据全等三角形的判定定理证明$\triangle AOB$与$\triangle DOC$全等,再根据全等三角形的性质求出$AB$的长度。
已知$O$是$AD$,$BC$的中点,所以$AO = DO=\frac{1}{2}AD$,$BO = CO=\frac{1}{2}BC$。
又因为$AD = BC = 10cm$,所以$AO = DO = BO = CO = 5cm$。
在$\triangle AOB$和$\triangle DOC$中:
$\begin{cases}AO = DO,\\\angle AOB = \angle DOC,\\BO = CO.\end{cases}$
根据全等三角形判定定理“边角边”($SAS$),可以得出$\triangle AOB\cong\triangle DOC$。
根据全等三角形的性质:全等三角形的对应边相等,因为$\triangle AOB\cong\triangle DOC$,所以$AB = CD$。
已知$CD = 4cm$,所以$AB = 4cm$。
【答案】:$B$。
已知$O$是$AD$,$BC$的中点,所以$AO = DO=\frac{1}{2}AD$,$BO = CO=\frac{1}{2}BC$。
又因为$AD = BC = 10cm$,所以$AO = DO = BO = CO = 5cm$。
在$\triangle AOB$和$\triangle DOC$中:
$\begin{cases}AO = DO,\\\angle AOB = \angle DOC,\\BO = CO.\end{cases}$
根据全等三角形判定定理“边角边”($SAS$),可以得出$\triangle AOB\cong\triangle DOC$。
根据全等三角形的性质:全等三角形的对应边相等,因为$\triangle AOB\cong\triangle DOC$,所以$AB = CD$。
已知$CD = 4cm$,所以$AB = 4cm$。
【答案】:$B$。
7. 立德树人·弘扬传统文化 在如图所示的部分象棋棋盘中,A处为点点的棋子“马”,B,C处为迅迅的两枚棋子,“马”可以从点A行棋至B处或C处吃掉迅迅的棋子,连接AB,AC,则$∠1+∠2= $
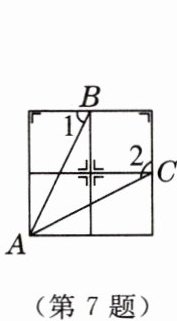
180
°.
答案:
180
查看更多完整答案,请扫码查看


