《2025年点拨训练八年级数学上册沪科版安徽专版》

1. [知识初练]如图①所示是我们生活中常见的晾衣架,其形状可以近似看成等腰三角形ABC(如图②),AB= AC.
(1)若∠B= 30°,则∠C= 30°；
(2)若∠A= 110°,则∠B= 35°.

答案： 【解析】：
本题主要考查等腰三角形的性质，即等腰三角形的两个底角相等，以及三角形内角和为$180^\circ$。
（1）已知等腰三角形$ABC$中，$AB = AC$，根据等腰三角形的性质，$\angle B = \angle C$。
题目给出$\angle B = 30^\circ$，所以$\angle C = 30^\circ$。
（2） 已知等腰三角形$ABC$中，$AB = AC$，根据等腰三角形的性质，$\angle B = \angle C$。
题目给出$\angle A = 110^\circ$，由三角形内角和为$180^\circ$，可以得到：
$\angle B + \angle C = 180^\circ - \angle A = 180^\circ - 110^\circ = 70^\circ$。
由于$\angle B = \angle C$，所以：
$\angle B = \frac{1}{2} × 70^\circ = 35^\circ$。
【答案】：
(1)$30$；
(2)$35$。

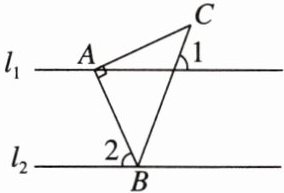
2. [2024·济南中考]如图,已知$l_1//l_2,△ABC$是等腰直角三角形,∠BAC= 90°,顶点A,B分别在$l_1,l_2$上,当∠1= 70°时,∠2= 25°.

答案： 解：过点C作CD//l₁，
∵l₁//l₂，
∴CD//l₁//l₂，
∴∠ACD=∠1=70°，∠BCD=∠2。
∵△ABC是等腰直角三角形，∠BAC=90°，
∴∠ACB=45°。
∵∠ACB=∠ACD - ∠BCD，
∴45°=70° - ∠2，
∴∠2=25°。
25°

3. [2025年1月合肥期末]如图,AB= AC= AD,∠BAD= 50°,则∠BCD的度数为 (D)

A.115°
B.130°
C.140°
D.155°

答案： 解：
∵AB=AC=AD，
∴∠ABC=∠ACB，∠ACD=∠ADC，∠ABD=∠ADB。
∵∠BAD=50°，
∴∠ABD=∠ADB=(180°-50°)/2=65°。
设∠ABC=∠ACB=x，∠ACD=∠ADC=y，
则∠BCD=x+y。
在四边形ABCD中，∠BAD+∠ABC+∠BCD+∠ADC=360°，
即50°+x+(x+y)+y=360°，
2x+2y=310°，
x+y=155°，
即∠BCD=155°。
答案：D

4. [2024·佛山月考]如图,已知AB= AC,AD是△ABC的外角∠EAC的平分线. 求证：AD//BC.

答案： 【解析】：
本题可根据等腰三角形的性质得出相关角的关系，再结合角平分线的性质得到角相等，最后根据内错角相等两直线平行来证明$AD// BC$。
步骤一：根据等腰三角形的性质得到角的关系
已知$AB = AC$，根据等腰三角形的性质：等腰三角形两底角相等，可得$\angle B = \angle C$。
步骤二：根据三角形外角的性质得到角的关系
因为$\angle EAC$是$\triangle ABC$的一个外角，根据三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角之和，所以$\angle EAC=\angle B + \angle C$。
又因为$\angle B = \angle C$，所以$\angle EAC = 2\angle C$。
步骤三：根据角平分线的性质得到角的关系
由于$AD$是$\angle EAC$的平分线，根据角平分线的定义：从一个角的顶点出发，把这个角分成相等的两个角的射线叫做这个角的平分线，可得$\angle EAD=\frac{1}{2}\angle EAC$。
结合$\angle EAC = 2\angle C$，可得$\angle EAD = \angle C$。
步骤四：根据平行线的判定定理证明$AD// BC$
因为$\angle EAD$与$\angle C$是内错角，且$\angle EAD = \angle C$，根据平行线的判定定理：内错角相等，两直线平行，所以$AD// BC$。
【答案】：
证明：
∵$AB = AC$，
∴$\angle B = \angle C$。
∵$\angle EAC$是$\triangle ABC$的一个外角，
∴$\angle EAC=\angle B + \angle C$。
又
∵$\angle B = \angle C$，
∴$\angle EAC = 2\angle C$。
∵$AD$平分$\angle EAC$，
∴$\angle EAD=\frac{1}{2}\angle EAC$。
∵$\angle EAC = 2\angle C$，
∴$\angle EAD = \angle C$。
∴$AD// BC$（内错角相等，两直线平行）。

5. [知识初练]如图,CD是等边三角形ABC的中线,如果AC= 5,那么BD= 2.5.

答案： 【解析】：本题主要考查等边三角形的性质以及中线的定义。
因为$\bigtriangleup ABC$是等边三角形，根据等边三角形三线合一的性质（等边三角形底边上的高、中线和顶角平分线三线合一），$CD$是$AB$边上的中线，所以$D$为$AB$中点。
又因为等边三角形三边相等，已知$AC = 5$，所以$AB=AC = 5$。
由于$D$是$AB$中点，那么$BD=\frac{1}{2}AB$。
将$AB = 5$代入可得$BD=\frac{5}{2}=2.5$。
【答案】：$2.5$

6. [2024·蚌埠二模]如图,一束平行光线照射在等边三角形上,若∠1= 40°,则∠2的度数为_________20°$.zyjl.cn/pic18/2025-07-18/848bdce914c9d2c7facf8f5eb00c737e.jpg?x-oss-process=image/crop,x_1431,y_1339,w_310,h_295">$

答案： 解：
∵△ABC是等边三角形，
∴∠BAC=60°。
∵光线平行，
∴∠1=∠BAC - ∠2（两直线平行，内错角相等）。
∵∠1=40°，
∴40°=60° - ∠2，
∴∠2=20°。
20°

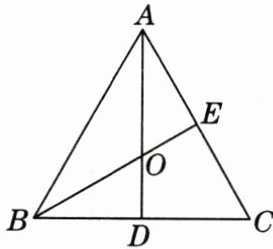
7. 如图,AD,BE是等边三角形ABC的两条角平分线,AD,BE相交于点O. 求∠AOB的度数.

答案： 【解析】：本题主要考查等边三角形的性质以及三角形内角和定理。
在等边三角形中，每个内角都是$60^\circ$。
由于$AD$和$BE$是等边三角形$ABC$的两条角平分线，
所以$\angle BAC$被平分为两个$30^\circ$的角，即$\angle BAD = \angle CAD = 30^\circ$。
同理，$\angle ABC$也被平分为两个$30^\circ$的角，即$\angle ABE = \angle CBE = 30^\circ$。
在$\triangle ABO$中，已知$\angle BAO = 30^\circ$，$\angle ABO = 30^\circ$。
根据三角形内角和为$180^\circ$，可以求出$\angle AOB$的度数：
$\angle AOB = 180^\circ - \angle BAO - \angle ABO = 180^\circ - 30^\circ - 30^\circ = 120^\circ$。
【答案】：$\angle AOB = 120^\circ$。